一类双曲型方程弱解的正则性

贺宣军,宋文静, 夏子伦，郑钟志，段 鹏

(云南民族大学 数学与计算机科学学院，云南 昆明 650500)

Sobolev空间理论的建立，使相关的其他学科(如泛函分析，实变函数，调和分析等)的知识恰当地应用到当代偏微分方程理论研究之中.当代偏微分方程解的研究总会在合适的泛函空间中考虑其弱解的性质，而Sobolev空间的引进(参看文献[1-2])则为这一研究提供了有效的方法.借助Sobolev空间，可以在更广泛的函数类中寻求方程的解，使得可解性变得容易，而这种解被称为“弱解”或“广义解”.本文给出了二阶双曲型方程

(1)

在一定假设条件下弱解正则性的研究.关于二阶双曲型方程弱解的正则性问题，很多学者已经作出了广泛的研究，如文献[2-4]的研究是在偏微分算子L的系数aij,bi,c光滑并且与时间t无关的条件下进行的.本文对系数的要求范围进行拓宽，使系数关于x光滑的同时与时间t有关，只要对系数稍加限制便可获得与文献[2]同样的结论.

1 准备知识

也就是说，与时间有关的偏微分算子L是满足上述已知条件的椭圆型算子，且L具有散度形式：

(2)

(3)

则得到(1)的弱解,这种求解方法叫做“Galerkin逼近法”.

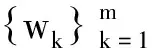
(4)

(5)

(6)

2 主要结果

定理1 ①设算子L系数满足aij(x,·),b(x,·),c(x,·)∈C1([0,T])，且假设函数

且

常数C与U,T及算子L的系数有关.

② 此外，如果

则有

u″∈L∞(0,T;L2(U))，u″∈L2(0,T;H-1(U))，

且

常数C与U，T及算子L的系数有关.

证明

(7)

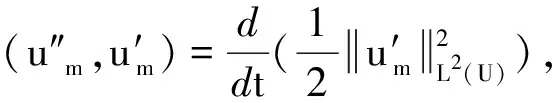
由aij=aji(i,j=1,2,…,n)，可得

(8)

由式(8)可得

(9)

同时有

综合以上不等式得：

(10)

又根据双曲型算子的条件可得A[u,u;t]的正定性,即

(11)

该不等式结合(10)式可得

(12)

可得

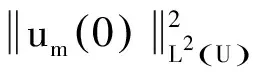
(13)

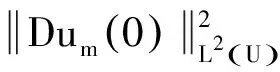
(14)

由(13)，(14)式得

(15)

现在记

(16)

把(16)式代人到(12)式得η′(t)≤C1η(t)+C2ζ(t)，a.e.0≤t≤T，根据Graonwall's不等式得

(17)

根据(4)，(5)，(15)式及A[u,v;t]的有界性可得

(18)

因此可由(16)～(18)式推出

因为0≤t≤T时t具有任意性，可由(11)式和上式推得

(19)

取极限(m=ml→∞时)，可得到①的结论.

(20)

(21)

特别有

由本步骤中上述几个不等式可推得

(22)

这里的双线型A[·,·;·]和前文定义的相同.

(23)

因为Δum=0， ∀x∈∂U所以B[um,-Δum]=(Lum,-Δum),接下来引用不等式:

(24)

可推得

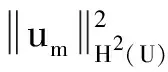
(25)

(26)

把(25)式应用于(26)式，根据Gronwall′s不等式可得

(27)

其中第2个不等式用到(6)式，第3个不等式用到(19)式和估计式[2]

取极限m=ml→∞时,可以得到u同样的有界性.

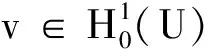
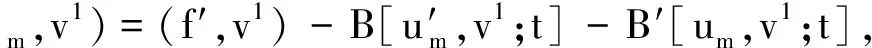
所以有

由定义可得

对上式关于t在区间[0,T]上积分并结合(27)式得

取极限m=ml→∞时，可得u‴∈L2(0,T;H-1(U))及和②的结论一样的关于u‴的估计式.

参考文献:

[1] 李立康, 郭毓騊. 索伯列夫空间引论[M]. 上海:上海科学技术出版社, 1981.

[2] FRIEDMAN A. Partial differential equations[M]. Michigan :RE Krieger Publishing Company, 1976.

[3] PYNCHON T. A survey of entropy methods for partial differential equations[J]. American Mathematical Society, 2004, 41(4): 409-438.

[4] HORMANDER L. The analysis of linear partial differential operators[M]//Distribution Theory and Fourier Analysis. New York: Springer-Verlag, 1983: 85

[5] 王术.Sobolev空间与偏微分方程引论[M]. 北京:科学出版社, 2009.

[6] FREIDLIN M I. Functional integration and partial differnetial equations[M]. Princeton: Princeton University Press, 1985.

[7] 董光昌. 线性二阶偏微分方程[M].杭州：浙江大学出版社，1987.

[8] DASKALOPOULOS P, HAMILTON R. Regularity of the free boundary for the 2 dimensional porous medium equation [J]. J Amer Math Soc, 1998, 11(4): 899-965.

[9] 王跃，何猛. Jaulent-Miodek方程组的精确解[J].云南师范大学学报：自然科学版，2013，33(3)：33-37.