可压缩磁化等离子体中量子效应对瑞利-泰勒不稳定性的影响

陆赫林

(云南民族大学 电气信息工程学院，云南 昆明650031)

量子等离子体是近期的一个研究热点，它在许多领域起到了重要的作用.如超微电子装置、致密天体等离子体[1-4]以及激光等离子体[5].当荷电粒子的德布罗意波长接近量子等离子体系统[6]尺度时，就必须要考虑在带电等离子体粒子中的量子效应.量子等离子体由电子、离子、正电子以及空穴构成.对量子等离子体的研究主要有3个著名的方程，分别是Schrödinger-Poisson方程， Wigner-Poisson 方程和量子磁流体力学方程.这些方程的详细讨论可参见文献[7—8].在量子等离子体中，这些方程广泛地用来研究等离子体粒子的统计和动力学行为.例如，在半导体物理中[9]，量子磁流体力学方程就用来描述电荷、动量和能量的输运.Haas扩展了量子磁流体力学方程来研究量子磁化等离子体以及运用Winger-Maxwell方程[10]导出了量子磁流体力学方程.

最近，量子等离子体系统中的瑞利-泰勒(RT)不稳定性的研究又受到广泛关注.在通常的流体力学中，当密度大的流体由密度小的流体支撑时，就会导致RT不稳定性的发生[11-12].微小的扰动就会导致流体的界面不稳定.在等离子体中，当致密等离子体受到磁场压力来抵消重力时，RT不稳定性就会发生.

有许多关于量子等离子体中磁流体动力学不稳定性的研究，特别是RT不稳定性[13-21].例如，Bychkov等[13]研究了量子效应对内波和RT不稳定性的影响.Brodin等[14]研究了经典区域的量子等离子体效应.Hoshoudy[15]研究了磁场中量子项对RT不稳定性的影响.Mondestov等[16]研究了量子等离子体中顺磁和铁磁性的RT不稳定性.Hoshoudy[17]研究了量子项对通过多孔介质的分层等离子体层的影响.Ali等[18]研究了非线性非均匀高密度量子等离子体中的RT不稳定性.以及，Cao等[19]研究了理想可压缩等离子体中，磁场对RT不稳定性的影响.笔者研究了无磁场的可压缩量子等离子体中内波和RT不稳定性[20].与此同时，邱孝明等[21]研究了Z箍缩等离子体中，可压缩效应对RT不稳定性影响，但没有考虑量子效应.所以，在文献[19-20]的基础上，在可压缩磁化量子等离子体中，对RT不稳定性进行了量子修正.

1 量子磁流体力学模型

假定等离子体是等温、良导电的可压缩流体.RT不稳定性由磁场的加速度来驱动，其中考虑了密度梯度.

连续和动量输运的量子MHD方程分别为：

(1)

(2)

绝热过程的状态方程为，

(3)

其中Vs是流体中的绝热声速.Maxwell方程为

(4)

(5)

Gauss定律可以作为Faraday定律的初始条件.量子普适欧姆定律为

(6)

在理想的MHD近似中，假定无限电导率，以及忽略方程(6)中的Hall力，即σ→∞，则方程(6)可化简为

(7)

方程(5)带入方程(2)中，得

(8)

对方程(7)取旋度，以及带入方程(4)中，得

(9)

平衡方程为

(10)

2 色散方程

(11)

(12)

(13)

(14)

(15)

(16)

(17)

扰动的坐标分量为：

(18)

(19)

(20)

(21)

(22)

(23)

其中，Qx1,Qy1和Qz1分别为：

(24)

(25)

(26)

(27)

色散方程(27)归一化为：

(28)

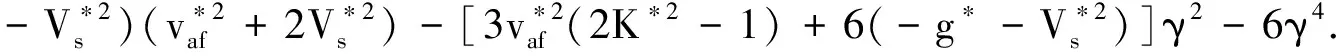
(29)

(30)

其中：

因此，我们得到归一化的RT不稳定性增长率的平方：

(31)

3 讨论

量子机制和平衡磁场对RT不稳定性的影响可以用方程(31)来讨论.

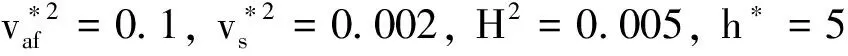
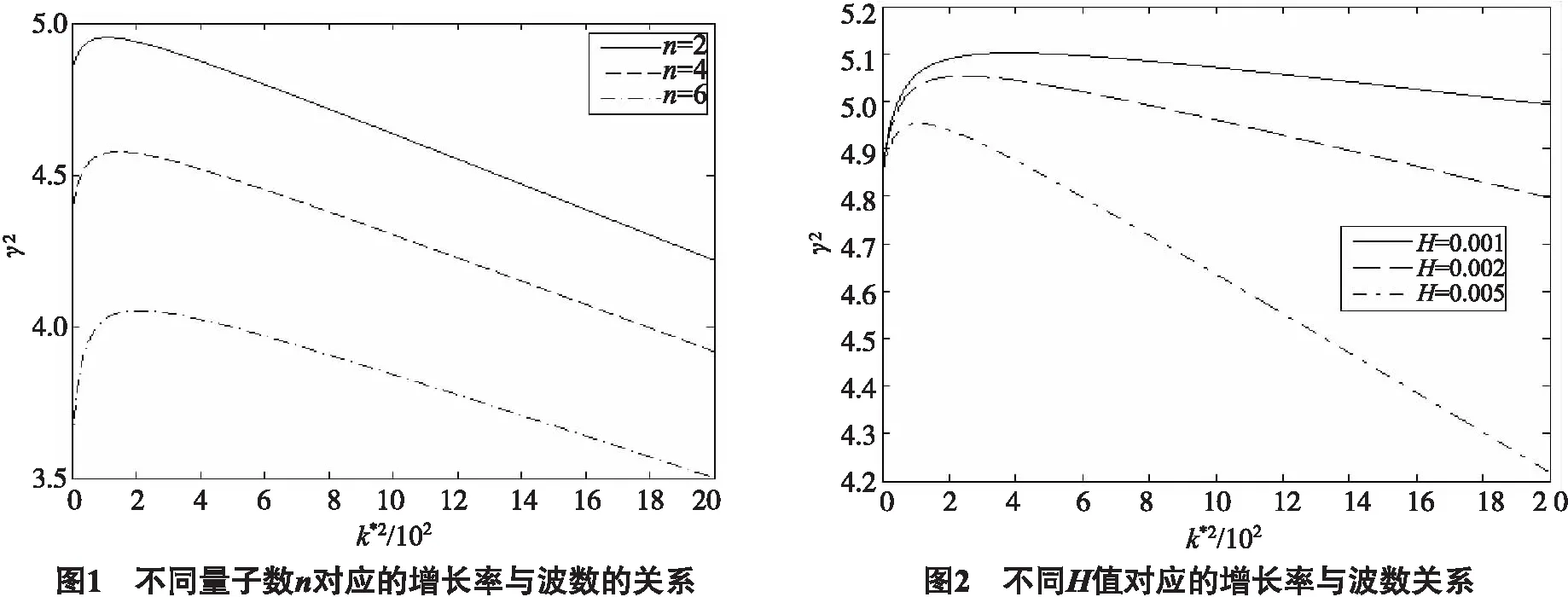
4 结语

笔者研究了约束在z=0 和z=h的2个平面内的可压缩层状等离子体中，量子机制和磁场对RT不稳定性的影响.通过对线性不稳定性的研究，以及对系统进行了求解，得到了量纲为1的色散关系.根据RT不稳定性色散方程的解，得到了RT不稳定性增长率，此增长率是归一化波数的平方K*2和平衡磁场的函数.通过以上研究得出：在可压缩磁化等离子体中，量子效应和平衡磁场都对RT不稳定性增长率起到抑制的作用，这和不可压缩磁化等离子体中的结果一致.即，量子效应和平衡磁场都会耗散可压缩磁化等离子体中的扰动能.

参考文献:

[1] MARKOWICH P A, RINGHOFER C A, SCHMEISER C. Semiconductor equations[M]. Vienna：Springer, 1990.

[2] CHABRIER G, DOUCHIN F, POTEKHIN A Y. Dense astrophysical plasmas[J]. Journal of Physics：Condensed Matter, 2002, 14(40)：9133.

[3] OPHER M, SILVA L O, DAUGER D E, et al. Nuclear reaction rates and energy in stellar plasmas：The effect of highly damped modes[J]. Physics of Plasmas, 2001, 8：2454.

[4]JUNG Y D. Quantum-mechanical effects on electron-electron scattering in dense high-temperature plasmas[J]. Physics of Plasmas, 2001, 8：3842.

[5] KREMP D, BORNATH T, BONITZ M, et al. Quantum kinetic theory of plasmas in strong laser fields[J]. Physical Review E, 1999, 60(4)：4725-4732.

[6] MANFREDI G. How to model quantum plasmas[J]. Fields Institute Communications Series, 2005, 46：263-287.

[7] HAAS F, GARCIA L G, GOEDERT J, et al. Quantum ion-acoustic waves[J]. Physics of Plasmas, 2003, 10：3858.

[8] MANFREDI G, HAAS F. Self-consistent fluid model for a quantum electron gas[J]. Physical Review B, 2001, 64(7)：075316.

[9] GARDNER C L. The quantum hydrodynamic model for semiconductor devices[J]. SIAM Journal on Applied Mathematics, 1994, 54(2)：409-427.

[10] HAAS F. A magnetohydrodynamic model for quantum plasmas[J]. Physics of plasmas, 2005, 12(6)：062117.

[11] RAYLEIGH L. Investigation of the character of the equilibrium of an incompressible heary fluid of variable density[J]. Proc London Math Soc, 1883,14:177.

[12] SAFFMAN P G, TAYLOR G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1958, 245(1242)：312-329.

[13] BYCHKOV V, MARKLUND M, MODESTOV M. The Rayleigh-Taylor instability and internal waves in quantum plasmas[J]. Physics Letters A, 2008, 372(17)：3042-3045.

[14] BRODIN G, MARKLUND M, MANFREDI G. Quantum plasma effects in the classical regime[J]. Physical review letters, 2008, 100(17)：175001.

[15] HOSHOUDY G A. Quantum effects on Rayleigh-Taylor instability in a vertical inhomogeneous rotating plasma[J]. Physics of Plasmas, 2009, 16：024501.

[16] MODESTOV M, BYCHKOV V, MARKLUND M. The Rayleigh-Taylor instability in quantum magnetized plasma with para-and ferromagnetic properties[J]. Physics of Plasmas, 2009, 16：032106.

[17] HOSHOUDY G A. Quantum effects on the Rayleigh-Taylor instability of stratified fluid/plasma through porous media[J]. Physics letters A, 2009, 373(30)：2560-2567.

[18] ALI S, AHMED Z, MIRZA A M, et al. Rayleigh-Taylor/gravitational instability in dense magnetoplasmas[J]. Physics Letters A, 2009, 373(33)：2940-2943.

[19] CAO J, REN H, WU Z, et al. Quantum effects on Rayleigh-Taylor instability in magnetized plasma[J]. Physics of Plasmas, 2008, 15：012110.

[20] LU H L, QIU X M. The internal waves and Rayleigh-Taylor instability in compressible quantum plasmas[J]. Physics of Plasmas, 2011, 18：104508.

[21] QIU X M, HUANG L, JIAN G D. Synergistic mitigation of the Rayleigh-Taylor instability in Z-pinch implosions by sheared axial flow and finite Larmor radius effect[J]. Physics of Plasmas, 2003, 10：2956.