基于模糊控制的RBF神经网络电力系统短期负荷预测
崔艳艳,程亚维
(济源职业技术学院a.电气工程系;b.信息工程系,河南济源 459000)
0 前言
近年来随着竞争机制的不断引入,我国的电力系统正由垄断经营阶段逐步向发电竞争阶段过渡,负荷预测工作也随之逐步发生转变[1]。负荷预测的重要性已经得到普遍重视,负荷预测的手段已由先前的人工预测方式逐步被软件预测方式所代替,负荷预测软件己成为能量管理系统(EMS)的重要组成部分[2]。另外,由于计算机的普及,使大量适用于电力市场环境下的负荷预测理论算法和预测模型的采用成为可能,为提高预测精度创造了有利条件。
目前,短期负荷预测的方法有很多种,神经网络和模糊理论预测方法受到国内外广大研究人员的高度重视,被认为是比较有效的方法[3]。在此背景下,本文针对电力系统短期负荷预测系统中的各种问题,进行了深入的探讨,建立基于模糊控制理论和RBF神经网络相结合的短期负荷预测模型,并对历史负荷数据及影响负荷的因素进行处理,通过实例验证了该预测模型的准确性。
1 RBF神经网络结构
径向基函数(Radial Basis Function,RBF)神经网络结构包括3层,依次按左、中、右的顺序分别为输入节点、隐节点、输出点,其网络结构如图1所示。每一层都有着完全不同的作用:输入层由信号源节点构成,其作用只是接受输入信号并将其传递到隐含层;隐含层由像高斯核函数那样的辐射状作用函数构成,是RBF网络中最重要的一层;输出层通常是对隐含层节点非线性基函数输出的线性组合,从而得到最后的结果[4-5]。
对于RBF网络的数学描述可表达为:在n维空间中,给定N个输入样本xi=(i=1,2,…,N),则网络隐含层的第k个节点的输出可以表示为:

其中,xi表示有n维输入向量;Tk表示第k个隐层节点的中心,k=1,2,…,l;· 通常为欧式范数; R(·)也表示RBF函数,它具有局部感受的特性,体现了RBF网络的非线性映射能力。而网络输出层的第j个节点的输出,则为隐含层节点到输出层的线性映射,即:
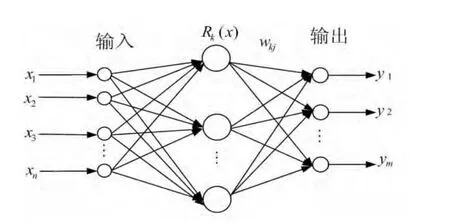
图1 RBF网络结构图

其中,wkj表示隐含层到输出层的权值;θj是第j个输出节点的阈值;m则是输出层的节点数。
2 基于模糊控制的RBF神经网络电力系统短期负荷算法
随着电力系统负荷的变化,RBF神经网络的内在关系也应发生变化,如果用原有的神经元网络参数进行负荷预测时,往往会产生较大的误差,但是模糊调整可以改变这种现象,提高负荷预测的精度。本文在进行电力系统短期负荷预测时,可以在RBF神经网络预测基础上再进行一个在线自调整的模糊控制。假设RBF神经网络的输出为U,模糊调整的输出为ΔU,则该网络预测的最后输出是Y=U+ ΔU,其预测流程如图2所示。
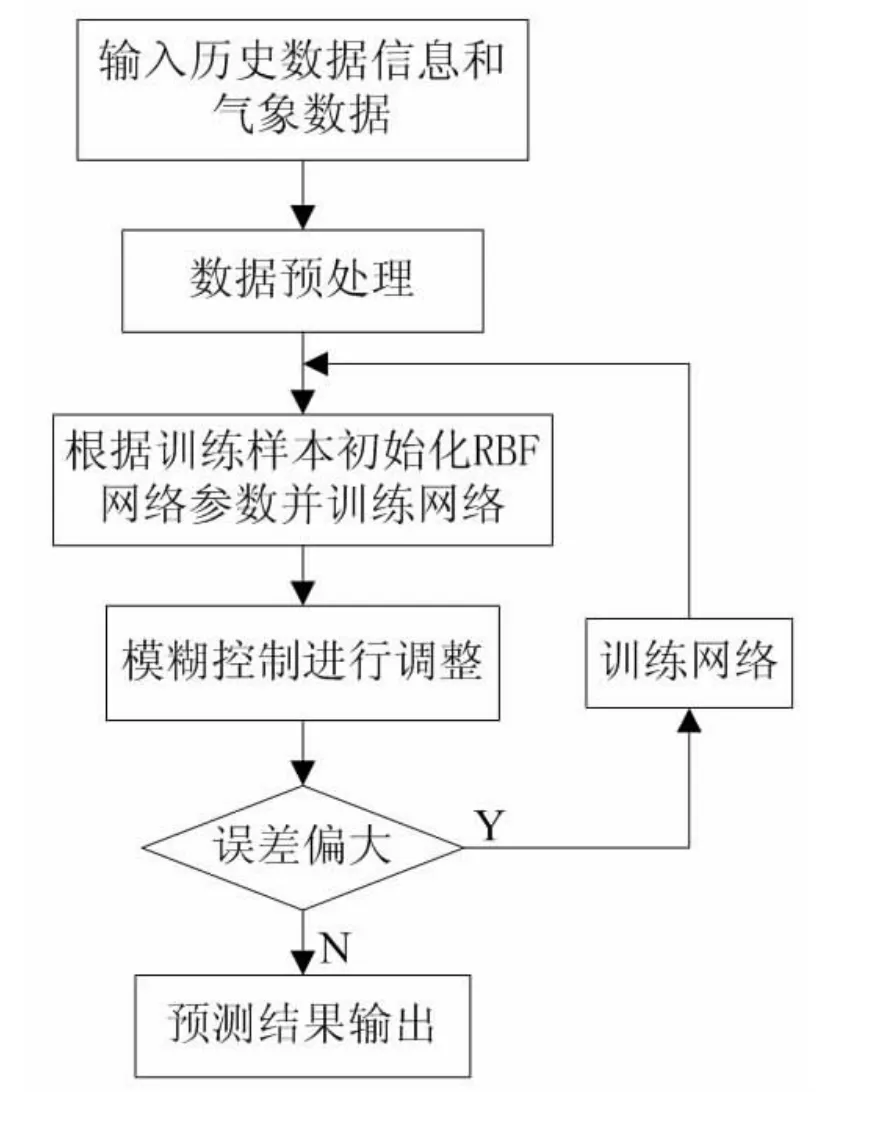
图2 模糊控制RBF网络预测系统工作流程
3 电力系统短期负荷预测实例分析
为了验证该方法的有效性和精确性,选取河南省某地区某天24小时内的电力负荷进行预测。本文建立24个RBF神经网络预测模型,每个神经网络的输入层节点为12个,隐含层节点为16个,输出层节点为1个。该算法并与传统的RBF神经网络算法进行比较,其负荷预测曲线如图3所示,相对误差曲线如图4所示。RBF和模糊控制RBF模型的预测数据进行对比,结果如表1所示。
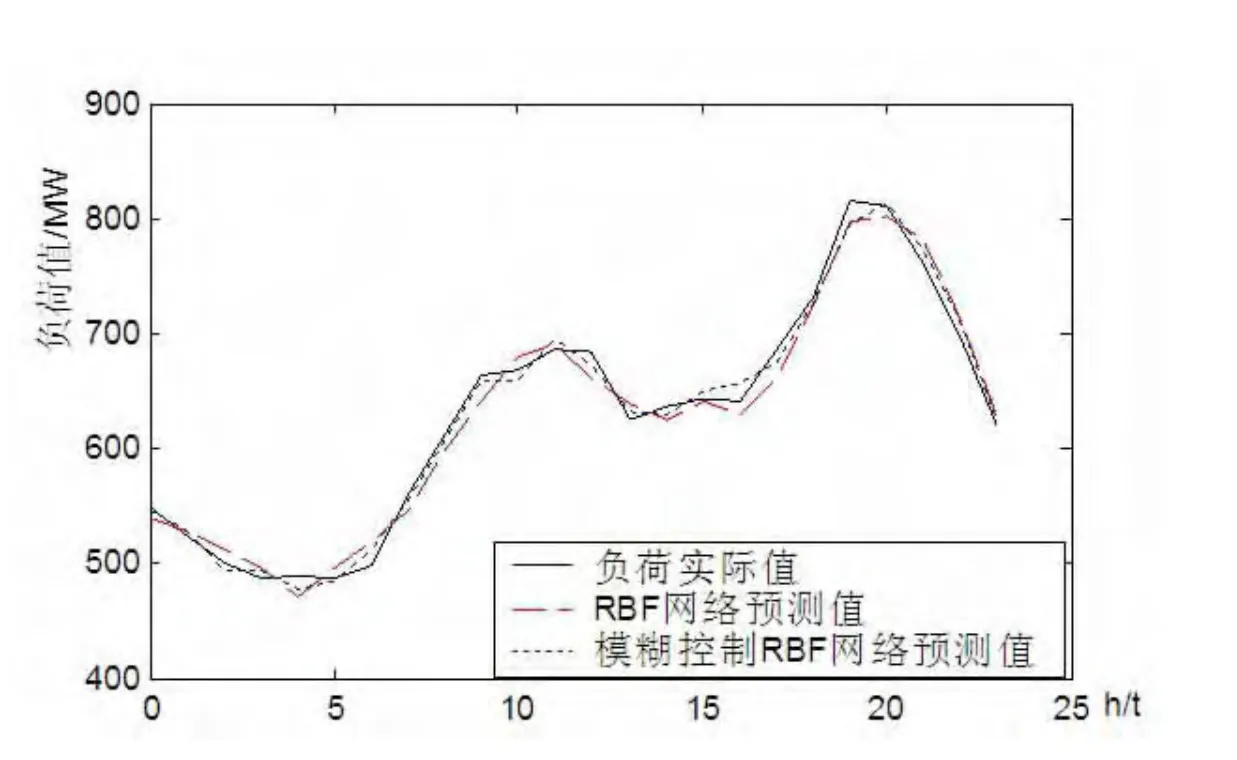
图3 RBF和模糊控制RBF模型的负荷预测曲线
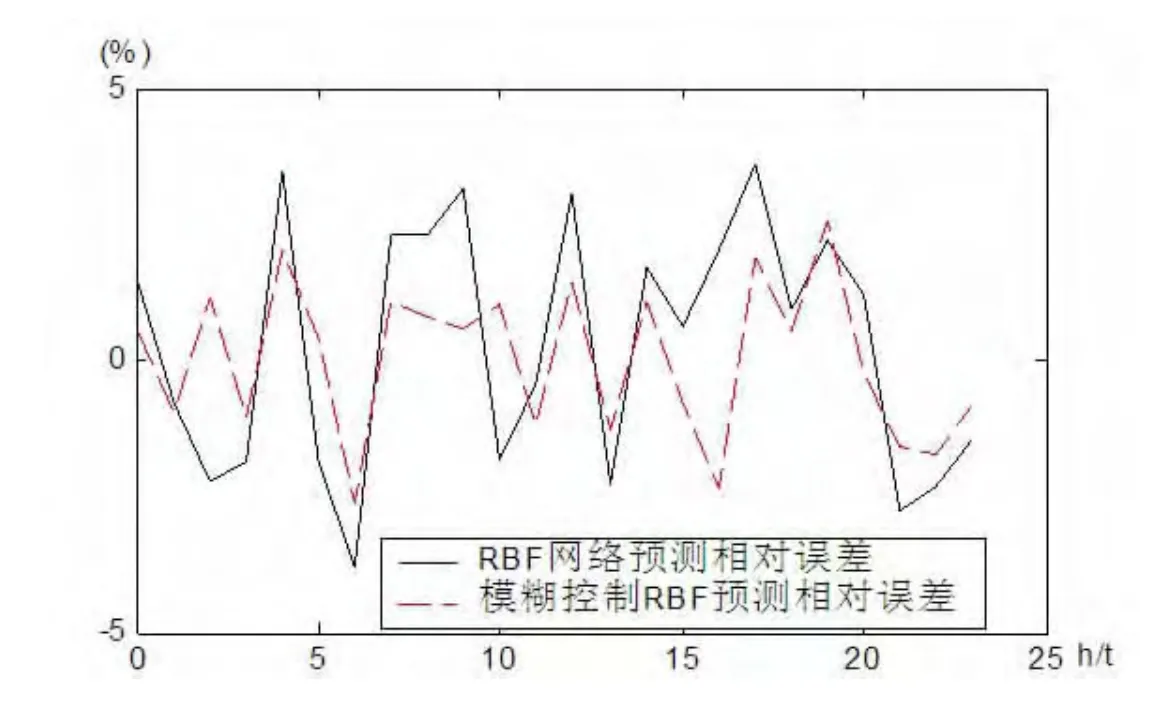
图4 RBF和模糊控制RBF模型负荷预测相对误差曲线
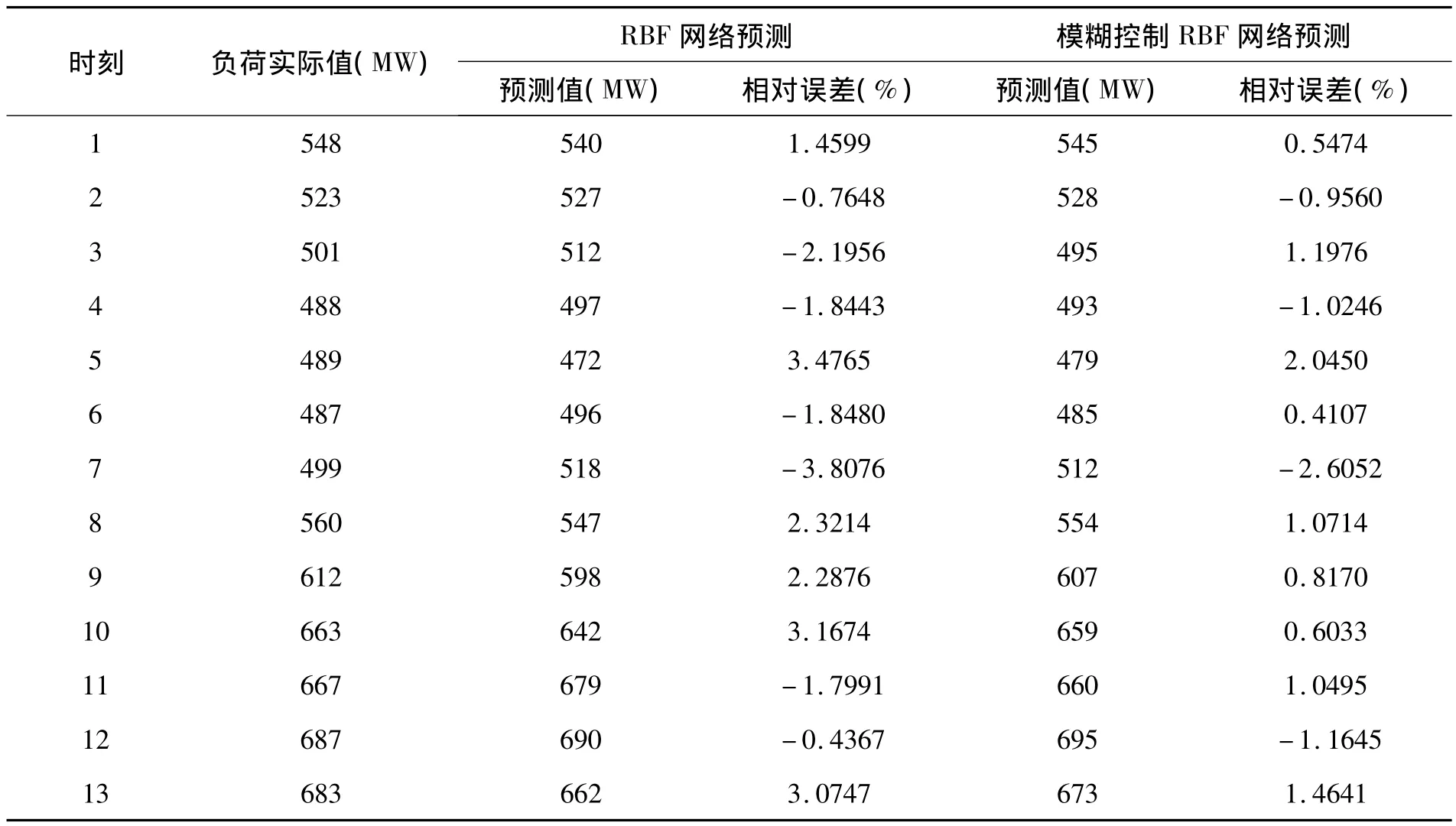
表1 RBF神经网络和模糊控制RBF神经网络模型的预测数据对比
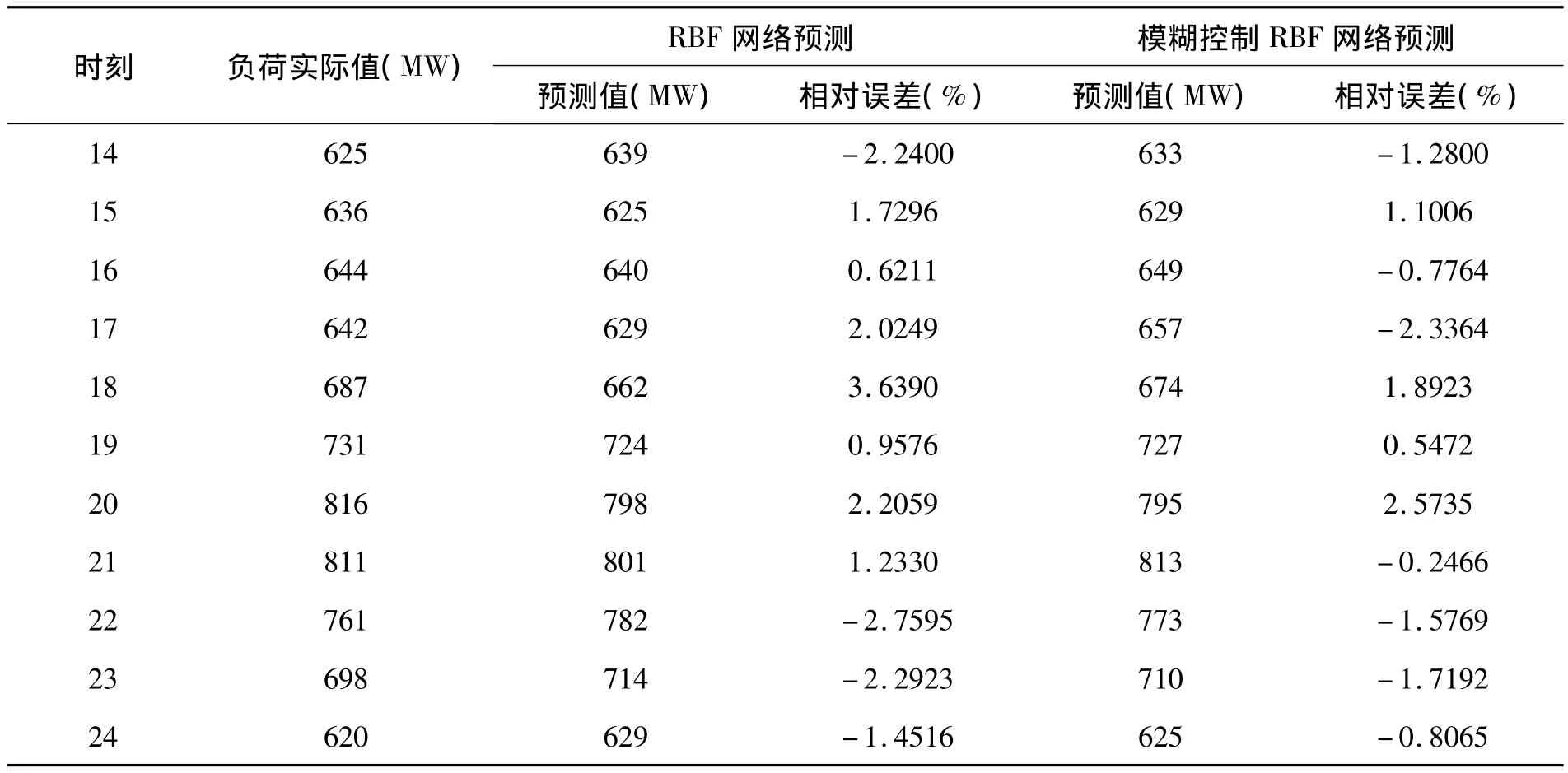
续表1
从表1中可知,RBF网络预测的最大相对误差为3.639 0%,最小相对误差为-2.759 5%;而模糊控制的RBF网络预测的最大相对误差为2.573 5%,最小相对误差为-2.605 2%。
4 结论
在电力系统短期负荷预测中,传统的RBF网络会产生较大的误差。本文提出模糊控制与RBF神经网络相结合的电力系统短期负荷预测算法,该算法是在RBF神经网络预测基础上进行在线自调整的模糊控制。结果表明,该方法与传统的RBF神经网络负荷预测方法相比,具有较高的预测精度。
[1]王黎明.电力系统中短期负荷预测的研究[D].东营:中国石油大学,2008.
[2]王聪.基于RBF神经网络与模糊控制的电力系统短期负荷预测[D].保定:华北电力大学,2004.
[3]张宁.基于模糊推理和神经网络的日负荷预测的研究[D].太原:太原理工大学,2006.
[4]刘昊,张艳,高鑫,等.基于RBF神经网络与模糊控制的短期负荷预测[J].电网与清洁能源,2009,25(10):62-66.
[5]李杨,李晓明,黄玲,等.基于人工神经网络和模糊集的电力系统短期负荷预测方法[J].华中电力,2007,20(2):1-4.

