youbot机械臂运动学及仿真
李毫亮,刘冠峰,曾 琦,邓明星
(广东工业大学机电工程学院,广东广州 510006)
0 引言
机械臂在工业自动化上有广泛的应用,对降低成本和提高效率方面有很重要的作用[1]。
要实现机械臂的平滑,稳定,精确等性能,首先要建立机械臂的运动学模型,运用D-H法进行运动学计算,并对运动空间进行预先仿真。为下一步机械臂轨迹规划、优化等方面建立基础。
1 D-H参数方程
D-H参数方程为计算机械臂前向运动学的基础,其通过D-H约定:轴Xi在空间垂直且相交于Zi-1[2]。按照此约定,连杆间变换关系可化简为公式如下:

其中:ai为沿Xi方向Zi与Zi-1间距离;
αi为垂直于 Xi平面Zi与 Zi-1间夹角;
di为沿 Zi-1方向 Oi与 Oi-1间的距离;
θi为垂直于 Zi-1平面Xi与 Xi-1间的夹角;
其中: cθi代表 cos(θi),sθi代表 sin(θ i ),sαi代表sin(α i),cαi代表 cos(α i).
2 运动学模型建立及计算
机械臂运动学计算是机器人运动学的基础,分为前向运动学和逆向运动学[3-4],在不考虑机械臂动力学的前提下,可通过机械臂运动学的计算,来仿真机械臂末端的可达空间;通过对逆向运动学的求解,可以得到各个变量的参数方程,为轨迹规划等建立基础。
此机械臂模型均为关节角为变量,在遵守D-H约定的前提下,建立其模型如图1所示。
2.1 正向运动学计算

图1 机械臂运动学模型
机械臂的正解问题即:已知机械臂的各个关节角变量,通过计算公式求得机械臂末端位置和姿态的过程。在此过程中只考虑机械臂的运动学问题,而不考虑机械臂的动力学等问题。由于本机械臂的各个参数已知,其各个参数如表1。


表1 机械臂参数
依据前向运动学公式,把以上各个相邻关节间的转换公式依次代入下列公式,可以得到如下的计算结果:
从而可以得到末端位置关系式:
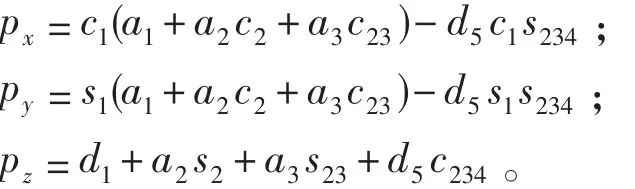
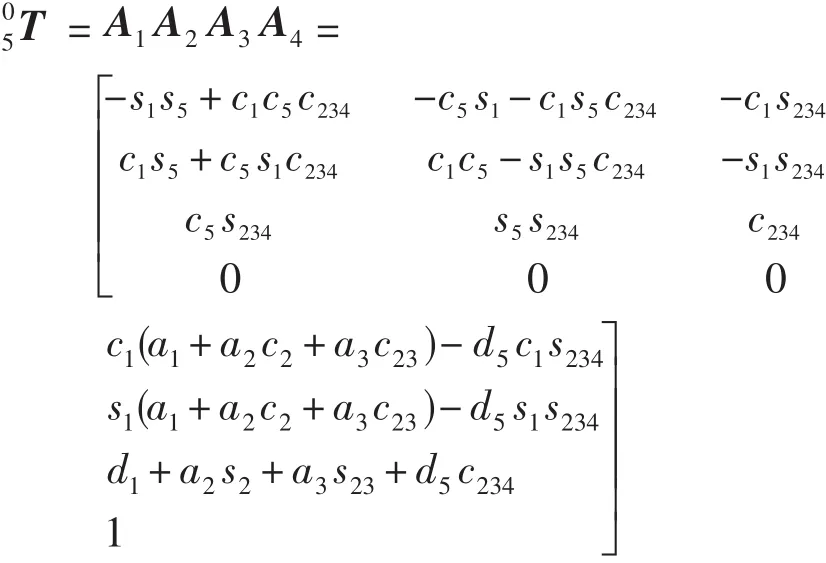
2.2 逆向运动学计算
其中:s1代表sin(θ1),c1代表cos(θ1),
s2代表sin(θ2),c2代表cos(θ2) , s5代表sin(θ5),c5代表cos(θ5),s23代表sin(θ2+θ3),c23代表cos(θ2+θ3), s234代表 sin(θ2+θ3+θ4) ,c234代表cos(θ2+θ3+θ4)。其余各参数含义见表1。
将各个参数带入上述公式可得:
机械臂的逆向运动学即:根据机械臂的末端位置和姿态方程式,求解各个关节变量的过程,由于机械臂末端位姿在已知的条件下,对应各个关节变量的解可能存在多组解的情况,所以在根据各项约束条件的情况下从多组解集中选出最优的一组解,为机械臂的轨迹规划、优化等建立基础。
现假设机械臂的末端位姿方程式如下:
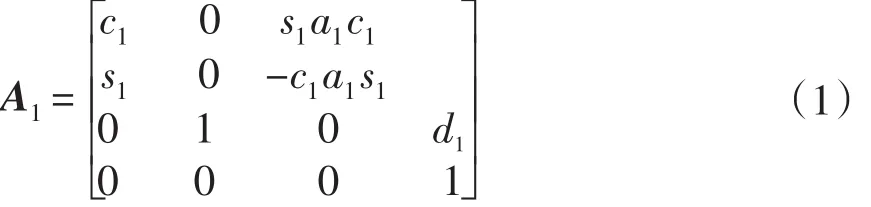
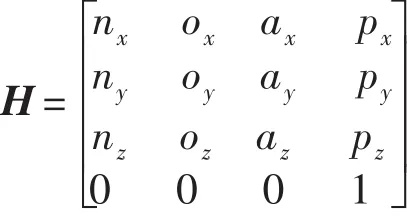
上式中前三列为机械臂在空间的位姿向量,最后一列为机械臂在空间的位置向量。
依据A-1H=A2A3A4A5,

由以上关系式中第三行、第四列对应项相等可得到:
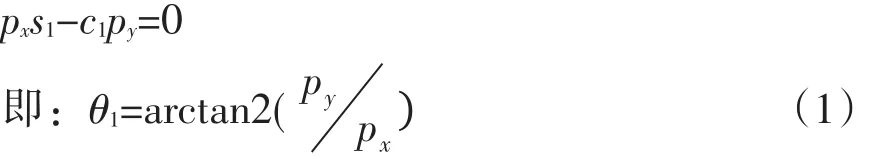
由关系式中第一行、三列与第二行、三列对应成比例可得到:

联合上式中第一行、四列和第二行四列可得到如下关系式:

化简求解得:
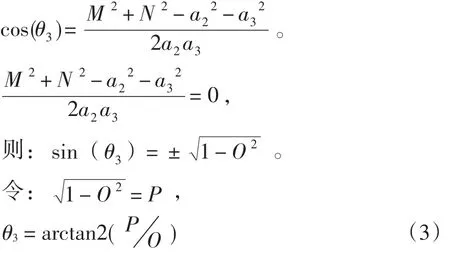
根据对应项还可以得到:
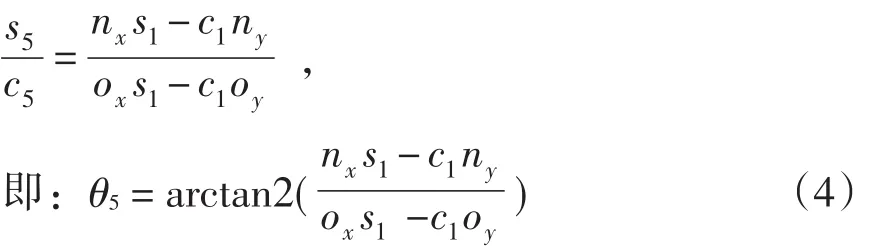
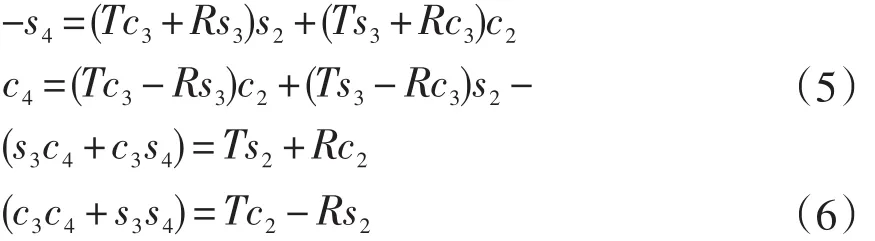
其中:T=az,R=axc1+ays1
联立(5)(6)得:

联立(2)、(3)、(7)得:

由以上关系式,最终求解出各个关节角函数关系式,由以上解集可知,对应于本结构的串联机械臂有多组解,通过结合杆件几何关系图2,根据机械臂初始位置和姿态,从多组解集中选择出一组最优化解集,为以后的机械臂轨迹规划、优化等建立基础条件等。
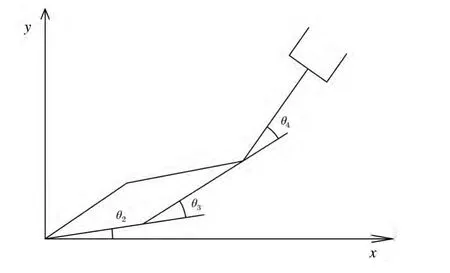
图2 三平行杆几何关系
3 Matlab仿真分析
由2.1中机械臂末端位置计算方程可知,此结构机械臂第五个关节角θ5的变化不影响末端在空间的可达空间,所以此仿真分析没有考虑θ5的变化。

其 中 a1=33, a2=155, a3=135, d1=75, d5=161,θ1的变化范围在±169°,θ2的变化范围在-65°到 90°之间,θ3的变化范围在-151°到 146°之间,θ4的 变 化 范 围 为 ±102.5°, θ5的 变 化 范 围在±167.5°。
上式为在2.1中的计算结果,依据此算法编写Matlab程序[5-6],以下各图θ1的角度均为 0°,其运行结果如图3所示。
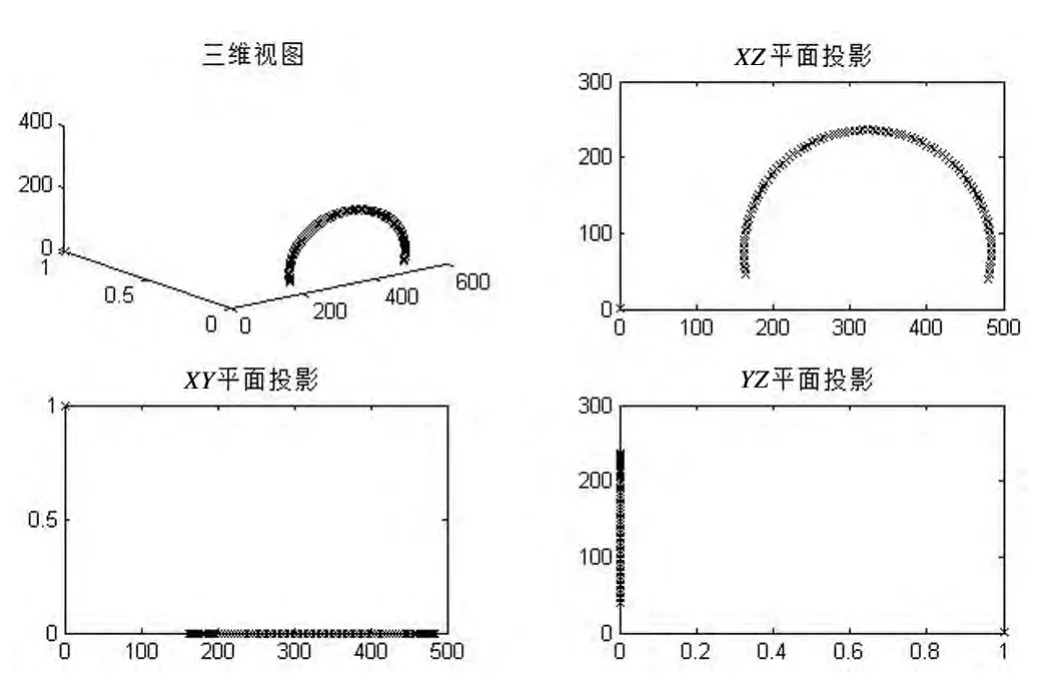
图3 θ4变化末端轨迹
由此图可以看出机械臂末端由θ4的变化引起,此轨迹为一整圆的一部分,其原因主要是由于角度4限制在±102.5°之间,还可以看出此圆弧的半径即为杆d5的长度。
此图为固定θ1、θ2仅仅在θ3、θ4变化下的轨迹,结合图2可以得到,图2为图3中的一条,当没有限制角度变化值的情况下,可知、两杆机构的空间轨迹唯一圆环,然而、由于各个角度均在其限定范围之内,所以此空间轨迹为圆环的一部分,其最外部分轨迹为两杆在一条直线上,最内部分轨迹为两杆空间距离最短时的轨迹。
此图为θ1为0°时,机械臂在平面XZ上的轨迹曲线,此轨迹即为此机构型机械臂在空间的可达空间,可以得到:由于各个角度的限制,在此圆形区域内,机械臂并非可以达到此空间中的每一点,所以、在机械臂轨迹规划是应通过合理的选择各个角度的变化,尽量避免机械臂在此空间的不可达点。

图4 θ3、θ4变化末端轨迹

图5 θ2、θ3、θ4变化末端轨迹
当θ1变化时,即为此图形绕d1杆运动,机械臂仿真运动空间与理论可达空间相同,验证了以上计算结果、算法的正确性。
4 结语
通过对Kuka robot机械臂建立运动学模型,进行前向运动学、逆向运动学计算,并通过Mat⁃lab软件对其运动空间进行了仿真,验证了计算结果的正确性。由于逆运算的多解性,所以需要根据条件选择一组比较合适的解集。为下一步移动机械臂的轨迹规划、优化等问题建立了前提基础。
[1]蔡鹤皋.机器人将是21世纪技术发展的热点[J].中国机械工程,2000(11):58-60.
[2] Mark W.Spong,Seth Hutchinson,and M.Vidyasagar.Robot Modeling and Control[Z].JOHN WILEY&SONS,INC.New York,2009.
[3]陈亚,沈晨.五自由度机械臂的运动学分析[J].北京石油化工学报,2013(1):25-28.
[4]吴挺,吴国魁,吴海彬.6R工业机器人运动学算法的改进[J].机电工程,2013(7):882-887,900.
[5]程立艳,费凌,苏泽郎.基于MATLAB五自由度机械手运动学仿真分析[J].机械研究与应用,2011(5):12-14.
[6]马如奇,郝双晖,郑伟峰.基于Matlab与Adams的机械臂联合仿真研究[J].机械设计与制造,2010(4):93-95.

