基于极点配置方法的扭转振动装置控制器设计

王佳伟，杨亚非，钱玉恒

(哈尔滨工业大学 飞行器控制实验教学中心,黑龙江 哈尔滨 150001)

Model205a型扭转振动装置是由世界知名的教学设备生产企业(美国ECP公司)生产制造的，已经在世界上500所大学中推广使用。该装置可以模拟单自由度、双自由度和三自由度系统的扭转振动特性，分析激励频率对系统固有频率的影响。此外，还可将其作为被控对象，进行控制算法的设计和仿真验证研究。本文将其配置成四阶的双自由度对象模型，推导其数学模型，设计极点配置控制器，并且通过仿真实验验证控制器的作用效果。

1 装置简介

实验装置的组成如图1所示。该装置有以下3个主要组成部分：

第1部分是扭转振动装置的机械部分，它由扭转机构、执行器和传感器构成，详细介绍见文献[11]。

第2部分是由M56000系列的DSP控制器板卡(见图2)和输入输出电箱组成的控制系统。DSP控制器能够以高采样率来执行控制律，解释轨迹命令，并支持数据采集、轨迹生成、系统状态及安全检测等功能。板卡中还包括可以实现编码器脉冲解码逻辑门阵列和2个进行实时模拟信号测量的辅助数模转换器(DAC)。控制器的板卡与实际工业控制中使用的板卡相同。电箱主要功能是为机械部分提供驱动电压，同时接收编码器的反馈信号，返回到控制器的板卡上，进而为执行程序提供测试数据。

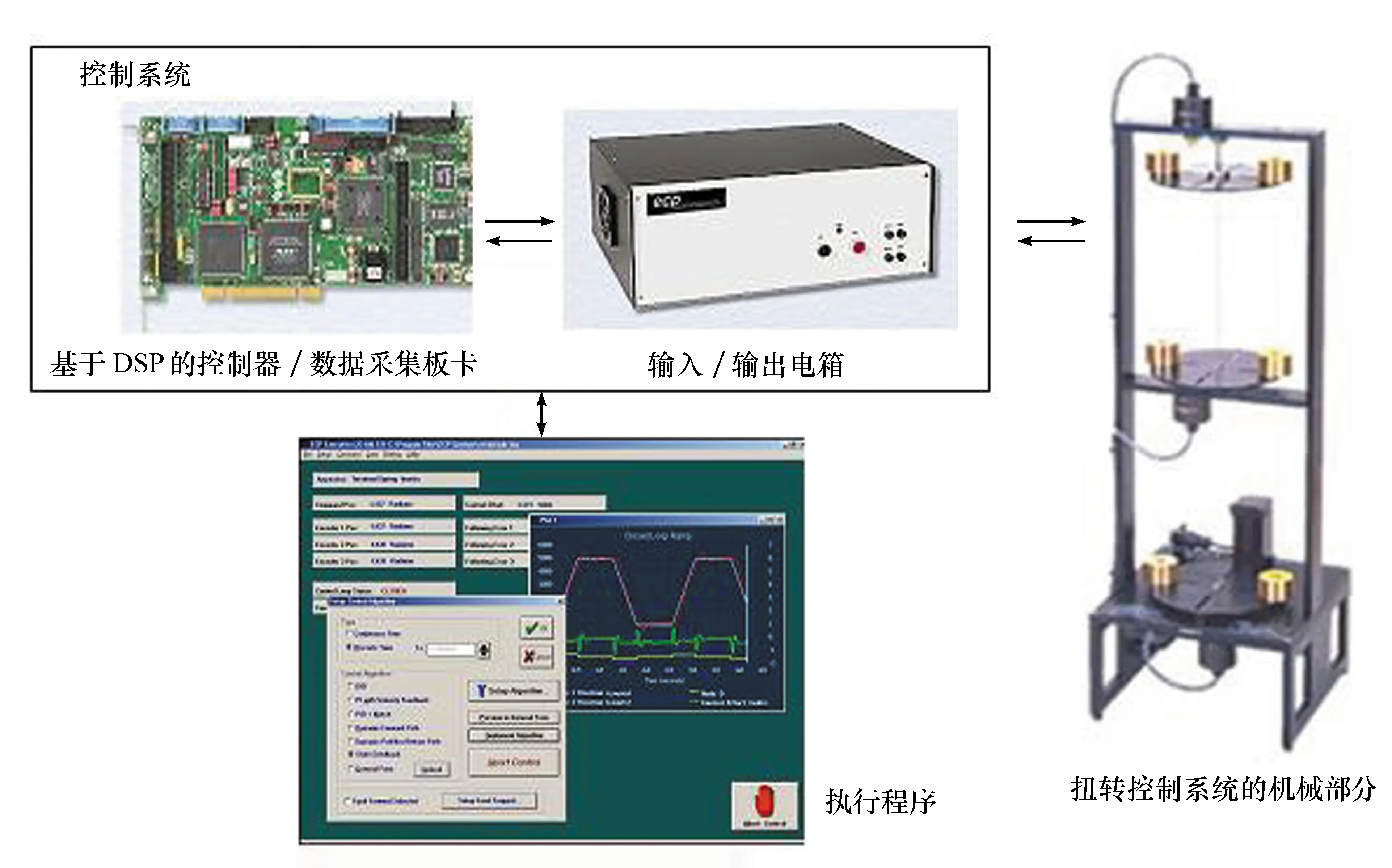
图1 扭转振动装置组成

图2 DSP控制器卡

第3部分是系统执行软件，即应用软件和用户界面，它支持控制器指定、轨迹定义、数据采集、绘图系统执行指令等功能。执行软件支持使用直观的“类C”语言来编写控制器算法程序，并且运行控制器。内置的自动编译器为执行程序代码提供有效传送和运行。此外，该执行软件还提供了与其他应用软件的接口，可以与Matlab软件进行连接调试。执行软件的运行窗口如图3所示。

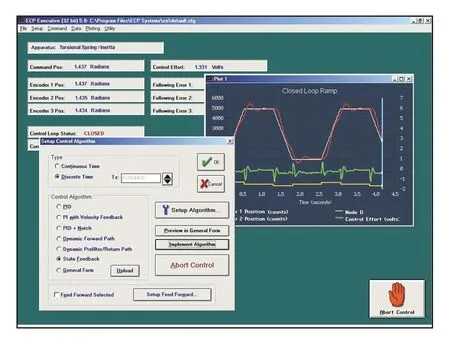
图3 执行软件的运行窗口界面

用户可以编写执行程序中的控制算法，然后将其加载到基于DSP的实时控制板卡上，DSP在每个指定的采样周期内执行此算法，读取参考输入和反馈传感器(光电编码器)的值，经过计算将数字控制效果信号输出到数模转换器(DAC)，数模转换器将数字流转换为模拟电压，然后通过一个伺服放大器转换为电流，再通过电机变为转矩，电机根据设备动力学特性将电机的输入转变为所期望的输出。设备完成指定的动作后，传感器的测试数据通过电箱回传到执行软件中，用于绘图和存储。

2 双自由度对象的模型推导

实验装置可配置为双自由度系统，如图4所示，忽略摩擦。输入为转矩T(t)，输出为第1个圆盘的角度θ1(t)和第2个圆盘的角度θ2(t)，2个圆盘的惯量分别为J1和J2，弹簧的弹性系数为k1，

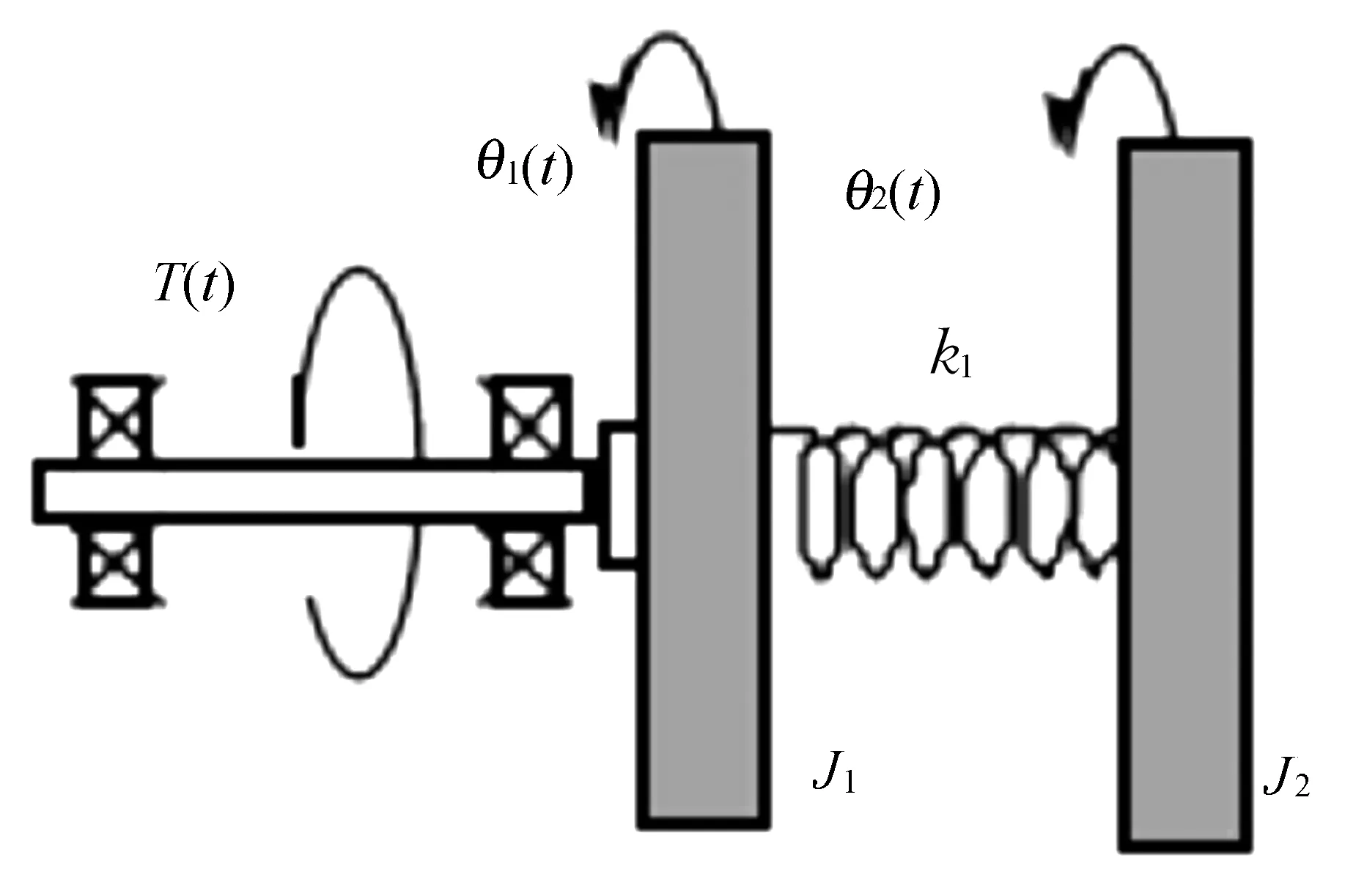
图4 双自由度对象模型

对2个圆盘进行受力分析及根据牛顿第二定律得到运动方程：

(1)

对上式两边取拉普拉斯变换，并假设初始条件为零，得到传递函数:

N1(s)=J2s2+k1

N2(s)=k1

D(s)=s2(J1J2s2+(J1+J2)k1)

(2)

用状态空间法表示：

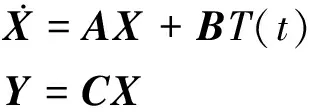
(3)

其中：

当Y=Xi,(i=1,2,3,4)且其余量为零时，Ci=1,(i=1,2,3,4)。

由数学模型可知，该模型为四阶二型系统，可以看成是刚体加一阶振荡模态组成，可以模拟单输入单输出、单输入多输出的系统。对于该模型的控制算法的研究，具有重要的应用意义。

3 极点配置控制器的设计及仿真验证

极点配置是一种利用状态或输出反馈，把线性系统的极点配置到预定位置，用来使闭环系统达到某种控制性能的控制律[12]。它的实质是用比例反馈去改变原系统的自由运动模式，以满足设计规定的性能要求。目前多数采用状态反馈和输出反馈方法可以实现极点的任意配置。例如对于某个线性定常系统 (A，B，C)，在采用反馈增益矩阵K实现状态反馈后，闭环系统就变成为(A+BK，B，C)。只要原系统(A，B，C)是能控的，则这样的反馈增益矩阵K就一定可以找到。反馈增益矩阵K的求解，对于单输入单输出情况，已有较为简单的计算公式；对于一般的多输入多输出情况，计算步骤要复杂得多，往往需要采用计算机来处理。

本节将对于双自由度的扭转控制装置，设计极点配置控制器来对其进行控制，并通过在装置上的仿真实验来验证控制律的有效性。

3.1 极点配置控制器的设计

如图5所示，双自由度系统等价为2个单自由度系统的串联，通过2个闭环结构来实现控制，同时在输入端加前置滤波器kpf/R(s)。在内环中考虑θ1(t)为被控量，则控制对象的模型为khwN1(s)/D(s)。然后为θ1(t)设计控制律，采用PD控制器kp+kds和低通滤波器af/(s+bf)，则内环的闭环传递函数为

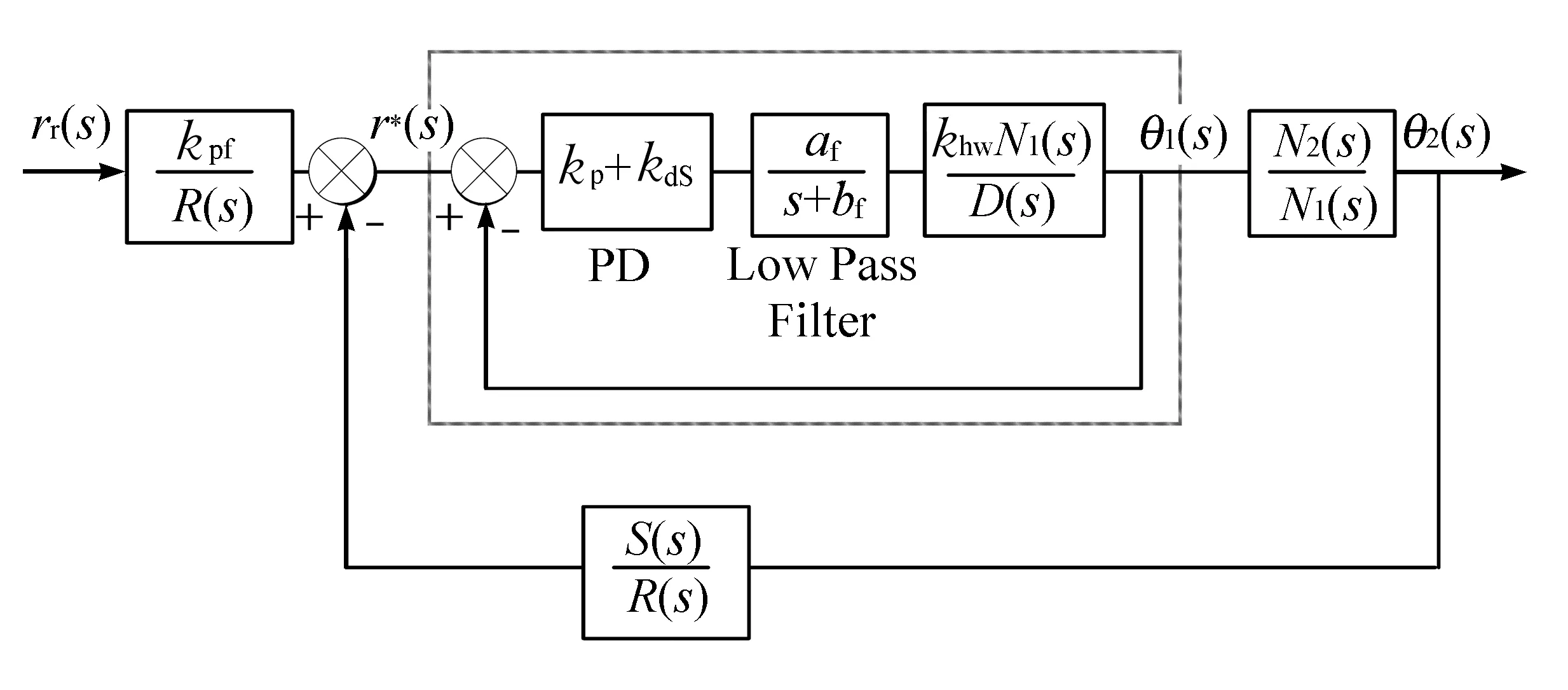
图5 极点配置控制器结构框图

(4)

需要设计参数使得内环等价为比例系数为1的环节。设计完内环的控制器之后再针对θ2(t)作为被控量，则外环的控制对象为

(5)

需要设计一个反馈控制器S(s)/R(s)以得到预期的闭环极点。则外环的闭环传递函数为

(6)

得到闭环特征多项式为

Dcl(s)=D*(s)R(s)+N*(s)S(s)

(7)

也可以表示为

Dcl(s)=(d2s2+d1s+d0)(r1s+r0)+

n0(s1s+s0)

(8)

式中，di和ni分别是公式(5)右边部分中分子和分母的参数，它们的值可由对象模型公式确定。ri和si代表反馈控制器的参数，是需要设计的。

假设期望的特征多项式为

Dcl(s)=(s+p1)(s+p2)(s+p3)

(9)

式中的pi即为期望的极点，是预先给定的参数。通过比较闭环特征多项式和期望特征多项式，就可以求出反馈控制器的参数ri和si。至此，完成了双自由度系统极点配置控制器的设计。

3.2 扭转振动装置的控制器参数的设计

本节的内容是为上一小节得到的控制器设计参数。N1(s)，N2(s)和D(s)由公式(2)给出，其中J1、J2、k1，以及装置的硬件增益khw均为已知。

首先按照单自由度的PD控制器设计方法进行内环PD控制器的设计，根据公式:

(10)

(11)

式中,fn为无限振荡频率,ζ为阻尼比。

设计PD控制增益，使fn=10 Hz，ζ=0.707。计算得到kp=2.5 ，kd=0.056。由于滤波器在s=-240(大约40 Hz)处有一个极点，并具有单位直流增益，解出滤波器参数af=240和bf=240。则内环总的控制器传递函数C内具有如下形式：

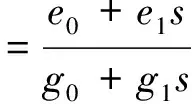
(12)

计算PD控制器和低通滤波器串联形成的控制器的分子和分母，得到e0=600，e1=13.3，g0=240，g1=1，即为内环的控制器参数，可知内环的开环放大增益近似等于1。

其次，计算外环反馈控制器，指定3个期望的极点为

(13)

则相应的期望特征多项式为

(14)

通过计算可得得到s0=-7.968 143，s1=3.492 598，r0=36.671 07，r1=1。计算出标量前置滤波器增益kpf=29.70，使输出θ2(s)匹配于输入rr(s)。

3.3 仿真验证

通过系统辨识的实验，可以确定khw,J1,J2,k1的值。将计算得到的PD控制器参数、低通滤波器参数、反馈控制器参数以及前置滤波器参数输入到软件中，得到一个双闭环的控制系统。

仿真步骤：设置输入幅值为1 000，持续时间为2 s，重复次数为1的阶跃信号；选择控制器类型为General Form，分别输入控制器参数，并加载到控制器中，设置数据采集，绘制编码器1、编码器3和命令位置的数据，得到对象的阶跃响应曲线见图6。

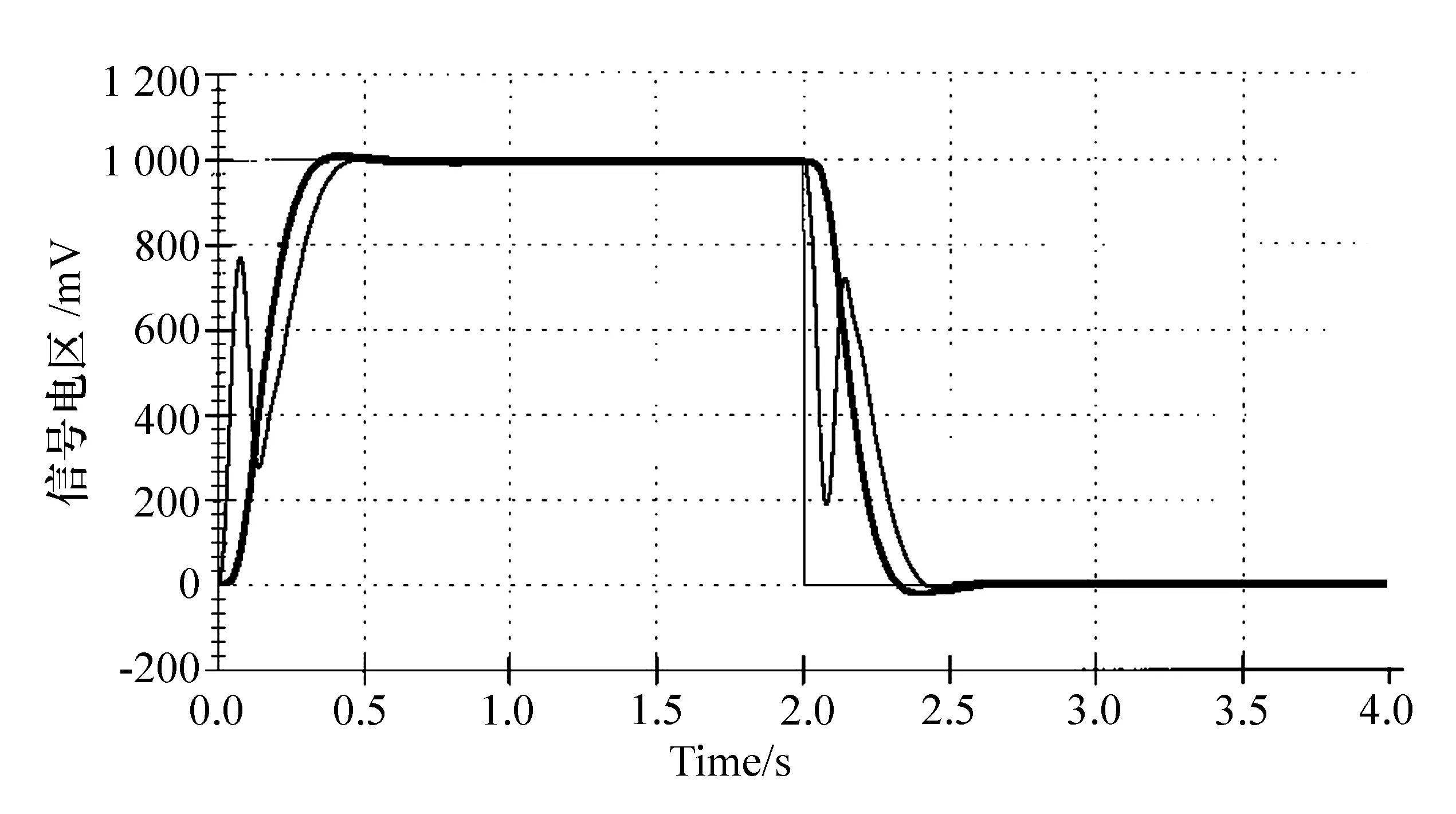
图6 极点配置控制器阶跃响应

由图6中的响应曲线可知，系统的超调量非常小，响应速度较快，证明所设计的极点配置控制器具有良好的控制性能。

4 结束语

本文首先对美国ECP公司的扭转振动装置的系统组成、性能和所能实现的功能进行概要介绍。然后对于该装置的一种等效的双自由度系统模型，设计了极点配置控制器，并验证了控制器的效果。本实验加深了对先进控制器设计方法的理解，为学生进一步学习更复杂的控制方法打下基础。

[1] 陈勇.汽轮发电机组轴系扭转振动测试[J].南京林业大学学报：自然科学版，2002,26(2):41-43.

[2] 陈锦涛.汽轮发电机轴系扭转振动固有频率计算数学模型[J].江苏电机工程，2004,23(1):60-62.

[3] 谢诞梅，刘占辉，杨长柱，等.汽轮发电机组轴系扭转振动对机械参数的敏感性分析[J].动力工程，2005,25(4):462-465.

[4] 王治国.汽轮发电机转子系统扭转振动及其控制过程研究[J].上海大中型电机，2007(2):22-23.

[5] 于学华.发动机曲轴系统扭转振动分析[J].汽车技术，2008(3):15-18.

[6] 张芳，王必璠，李显戴.车用发动机扭转振动的分析与控制[J].汽车科技，2011(2):47-51.

[7] 上官文斌，陈超，段小成，等.发动机曲轴系统扭转振动建模与实测分析[J].振动测试与诊断，2012,32(4):560-568.

[8] 周金宇，陈占福.粗轧机主传动扭振分析[J].钢铁，2007,42(5):51-54.

[9] 王勤.轧机主传动系统的扭振分析与建模[J].冶金设备，2009(4):6-9.

[10] 刘浩然，张业宽，李晓梅.轧机非线性传动系统冲击扭振的研究与抑制[J].振动与冲击，2010,29(7):179-183.

[11] 王佳伟,杨亚非,钱玉恒.基于扭转振动装置的PID实验设计[J].实验技术与管理,2014,31(3):59-62.

[12] 易宜连.极点配置法在工程控制设计中的应用[J].华东交通大学学报，1985(2):50-65.