有源调谐混合滤波器的改进无差拍控制策略研究

邓亚平, 同向前, 鲍洋, 冯颖

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

将有源补偿技术与无源电力滤波器相结合构成的混合电力滤波器兼备有源电力滤波器与无源电力滤波器各自的优点[1-2]，是目前高压大容量电力滤波器的发展方向。分布式电源接入是未来智能电网的主要特征之一[3-4]，但目前的混合电力滤波器在对有源装置APF部分进行控制时都需要检测系统的负荷电流或电源电流[5-7]，因而难以适应于含有分布式电源与分布式非线性负荷的智能电网发展需求。

针对微电网的分布式特征，文献[8-9] 提出了一种可应用于微电网中且具有优良滤波效果的有源调谐型混合电力滤波器。其中，有源装置APF部分的控制是基于检测流过滤波支路电流的有源调谐控制方法，这种控制方法不同于以往混合滤波器中APF的控制，它不需要采集滤波器本身之外的任何信号，即不需要检测负载电流或电源电流，因此可应用于任何输配电系统中，特别是新兴的微电网的谐波抑制。在这种混合滤波器中用于有源调谐控制的谐波补偿系数的实时调整是实现谐波抑制的关键技术之一。文献[8-9] 所采用的有源调谐控制方法中，谐波补偿系数是基于PI控制器对滤波器失谐度的参考值与实际值之间的误差信号进行运算处理后得到的，因此PI调节器参数的选择对系统谐波补偿性能的影响较大。然而，考虑到滤波系统实际运行工况和延时等因素，PI参数的获取较为繁琐复杂。

为了克服有源调谐型混合滤波器目前所采用控制方法中PI参数整定过程复杂的缺点，本研究结合有源调谐型混合电力滤波器的工作原理，在原有控制策略的基础上提出了一种新型控制方法。本研究首先对改进无差拍控制策略进行了理论分析，然后，通过仿真分析与实验验证，证明了该改进无差拍控制方法的正确性与可行性。

1 原有控制策略所存在的问题

有源调谐型混合电力滤波器(Active Tuned Hybrid Power Filter—ATHPF)是由传统单调谐滤波器和有源滤波器有机结合而成的，其中APF是并联于电抗器两端且作为受控电流源工作的。当ATHPF对电网中的h次谐波电流进行补偿时APF的输出电流iAPF.h应满足：

iAPF.h=Kh·iFh

(1)

式中，Kh为APF对h次谐波的补偿系数，iFh为注入滤波器中的h次谐波电流。

前期的研究结果已经表明[8]，此时在h次谐波频率下滤波电抗器的等值电感Leq.h为：

Leq.h=(1+Kh)L

(2)

其中，L为滤波器的初始电感值。

显然，通过对Kh值的合理控制可以实现ATHPF的谐波抑制功能。调整Kh值的目的在于使ATHPF完全调谐，即滤波器的失谐度0，因此选择滤波器的失谐度做为调节Kh值的依据。

文献[8-9] 给出了一种可行的Kh调节方法。如图2所示，控制系统在实时检测到滤波器的实际失谐度δ后与失谐度参考值δ*进行做差比较，进而经PI调节器后可生成相应的谐波补偿系数Kh。将控制得到的谐波补偿系数Kh与滤波支路中的h次谐波电流iF.h相乘便可得到APF参考电流iAPF.ref。最后由PWM发生器生成用于控制APF的PWM信号。

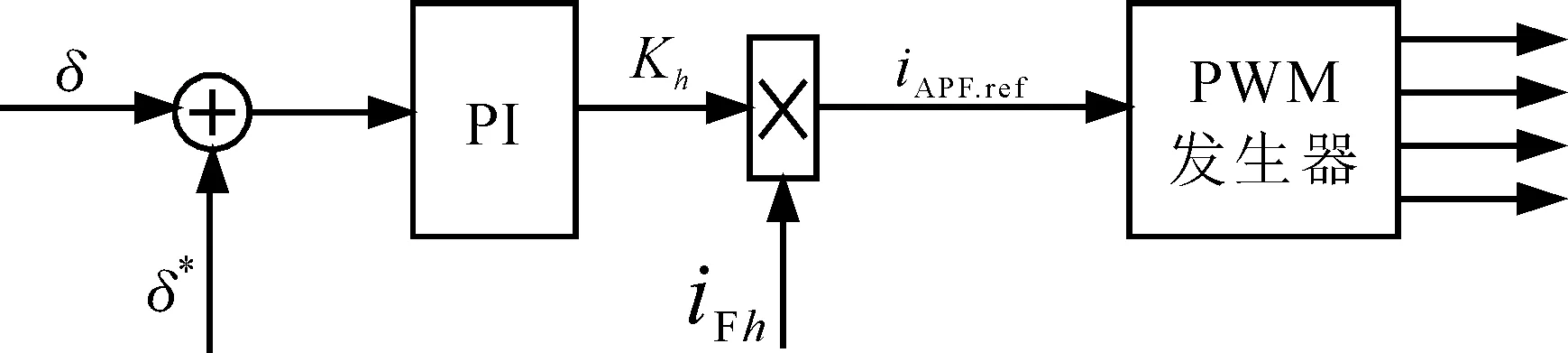
图1 原有控制策略中Kh的闭环控制方法

图1中Kh实现的一个重要环节就是滤波器实际失谐度δ的实时测量。失谐度的检测是ATHPF实现滤波的基础，检测精度也是影响滤波器性能和运行稳定性的重要因素。本研究采用式(3)来对滤波器的失谐度进行检测，即:

(3)

式中，ULh、UCh分别为滤波器中滤波电抗器和滤波电容器上h次谐波电压的幅值。

显然，若忽略电抗器的附加电阻，当滤波器完全谐振时，也即在滤波器h次谐波理论失谐度为0时，电抗器与电容器上的h次谐波电压幅值相等，式(3)所示失谐度测量值等于零，当滤波器失谐越大时，式(3)所示失谐度测量值也越大，且其正负反映了失谐的方向。由于在滤波器失谐度接近于0时，ULh、UCh达到了最大值，因此式(3)所示失谐度检测方法可以实现失谐度的无盲区检测。

设滤波器中滤波电感与电容分别为L、C，滤波器的实际谐振角频率为ωr，则：

(4)

设电网h次谐波角频率为ωh，按照失谐度的定义，滤波器对h次谐波的理论失谐度δ0为：

(5)

假设滤波器中滤波电抗器与电容器的h次谐波阻抗分别表示为XLh、XCh，则在忽略滤波电抗器等值电阻时，δ的表达式为：

(6)

将式(4)、式(5)代入式(6)，可得失谐度测量值δ与理论失谐度δ0之间的关系为：

(7)

考虑到在失谐度的通常变化范围内，即-0.2≤δ0≤0.2时，有：

(8)

式(8)表明，由式(3)检测得到的滤波器失谐度能够准确反映滤波器的实际失谐度。

ATHPF在实现系统h次谐波抑制功能时，失谐度的参考值δ*应设为0，因此在检测得到滤波器的实际失谐度后，有源调谐系数Kh值可按图1给出的控制方法来获得。如图1所示，Kh值是通过对滤波器失谐度的参考值δ*与实际值δ的误差进行PI调节后得到的。PI控制器的跟踪原理在于将δ*与δ的误差输入信号通过比例积分处理，进而得到相应的谐波补偿系数Kh。

然而，在该控制方法中PI调节器的参数选择对系统的滤波性能影响较大。文献[10] 中给出了不考虑系统延时图1所示控制方法中的PI调节器参数选择方法，因此PI控制器的参数计算结果具有一定局限性。但若考虑滤波系统的实际运行工况及控制系统中所存在的延时等因素，将会使PI控制器的参数整定过程更加繁琐复杂。此外，文献[10] 中分析计算出的PI调节器比例系数和积分时间常数整定结果均为一取值范围。在实际应用中还需对计算得到的PI控制器参数进行适当调整才能获得理想的滤波效果。

2 ATHPF的改进无差拍控制策略

为了克服ATHPF原有控制策略所存在的问题，本研究在不影响系统谐波抑制效果的前提下提出了一种可替代图1所示的原有控制策略中PI调节器的改进无差拍控制方法。

该控制策略在由式(3)检测得到滤波器实时失谐度后进一步经过运算处理便可得到相应的各次谐波补偿系数。

2.1 理论分析

结合ATHPF对h次谐波抑制的工作原理可得：

(9)

其中，C为滤波电容器的电容量。

结合式(2)、式(5)和式(9)可得失谐度理论值δ0与h次谐波补偿系数Kh之间的关系，即：

Kh=(1-δ0)2-1

(10)

联立式(7)、式(10)可推算出失谐度测量值δ与补偿系数Kh之间关系为：

(11)

因此，在控制系统根据式(3)检测得到滤波器的失谐度测量值δ后通过式(11)可以计算得到相应的h次谐波补偿系数Kh的值。

图2给出了δ在[-0.2,0.2]区间变化时式(11)所示的失谐度测量值δ与补偿系数Kh的关系曲线。

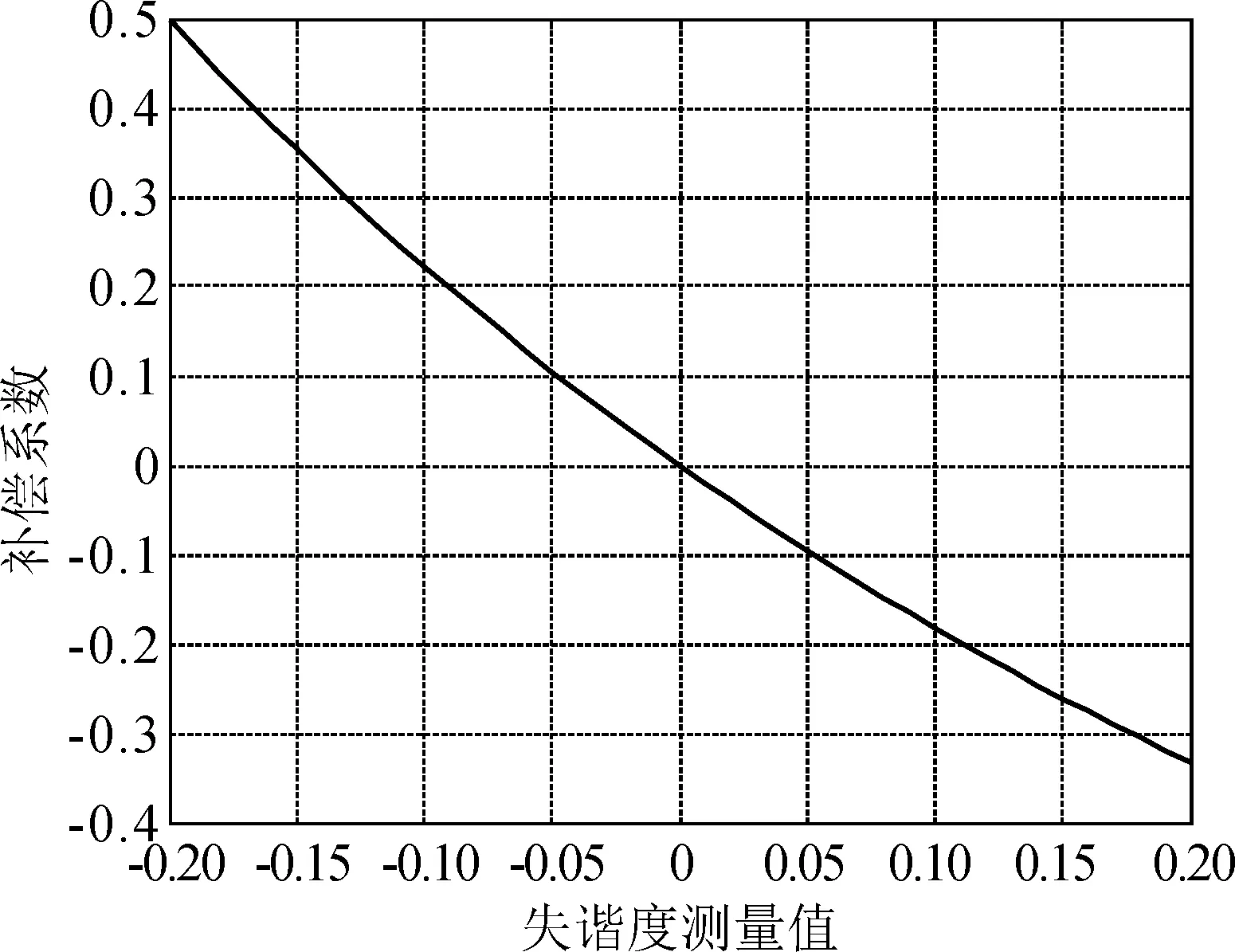
图2 失谐度测量值δ与补偿系数Kh的关系曲线

表1以三次谐波为例，在滤波电容器取为75 μF，滤波电抗器取不同值时理想补偿系数与计算补偿系数的计算结果对比。其中，理想失谐度δ0由式(5)计算所得，测量失谐度δ由式(7)计算所得，理想补偿系数由式(2)计算所得，计算补偿系数由式(11)计算所得。

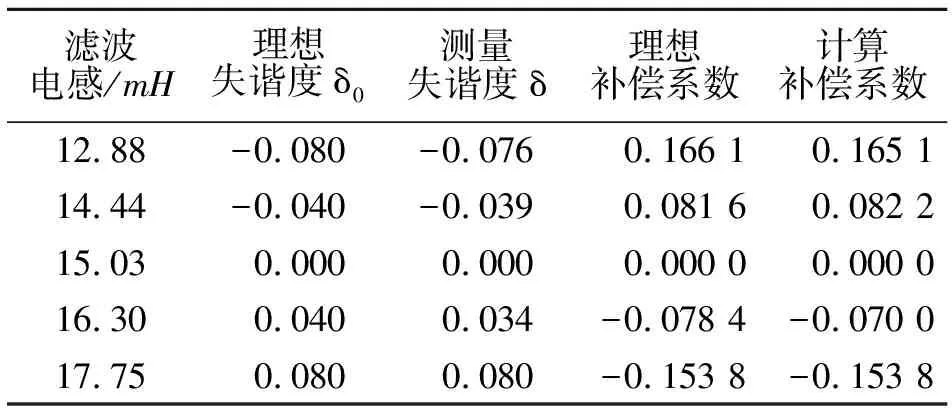
表1 理想补偿系数与计算补偿系数结果对比

通过表1可以看出，根据式(11)计算所得到的补偿系数与理想补偿系数之间是完全吻合的，并且当滤波器失谐较小时，计算出的实际补偿系数仍然具有较高的检测精度。此外，补偿系数的理想值与计算值之间的偏差很小，可以忽略不计。

2.2 算法实现

令Kh.0为滤波系统补偿h次谐波时所需的理想补偿系数，Kh(t-1)为上一时刻的实际补偿系数，Kh(t)为本时刻的h次谐波实际补偿系数，ΔKh为上一时刻实际补偿系数与理想补偿系数之间的偏差。

结合式(6)可进一步得到：

(12)

结合式(10)、式(12)可得：

(13)

联立式(11)、式(13)可得：

(14)

由于补偿系数的取值范围为(-1,1)，因此式(14)中的分母为一正值。若上一时刻得到的h次谐波补偿系数小于期望值，即Kh(t-1)Kh.0，ΔKh为负增益；当Kh(t-1)=Kh.0，则ΔKh为零。

至此，利用Kh(t-1)便可得到下一时刻Kh(t)的值为滤波系统补偿h次谐波所需的理想补偿系数时需满足的条件：

(15)

因此，根据上一时刻的实际谐波补偿系数Kh(t-1)，按式(15)所计算出的下一时刻补偿系数Kh(t)即为期望的h次谐波补偿系数Kh.0。

为了便于算法实现，可近似假设为：

m=1+Kh(t-1)

(16)

其中m>0，为一常量，且取小于采样频率的值。

故式(15)可以简化为：

y(z)=z-1·y(z)+m·u(z)

(17)

即：

(18)

其中，y(z)为输出量，u(z)为输入量。

通过上述分析可得补偿系数生成原理如图3所示，其输入量为控制系统根据式(3)计算所得h次谐波失谐度的测量值δ，输出量为补偿系数Kh(t)。

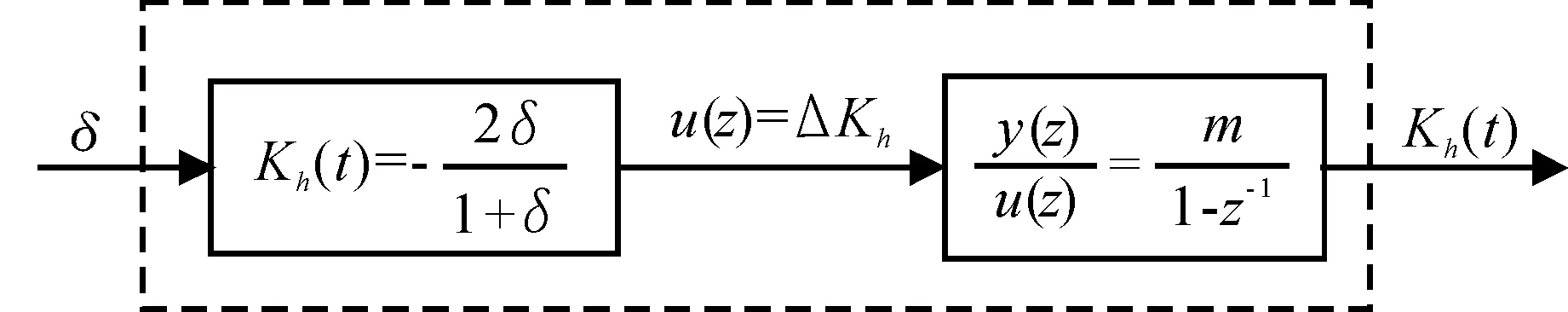
图3 改进无差拍控制策略中补偿系数实现框图

3 仿真与实验结果

3.1 仿真结果分析

为了验证上述理论分析的正确性，建立了基于改进无差拍控制策略的三相ATHPF仿真系统。仿真系统由电源、非线性负荷和ATHPF共同构成。其中，非线性负荷由5、7、11和13次谐波电流源共同构成，ATHPF由无源滤波器和有源滤波器共同构成，具体的系统仿真参数如表2所示。

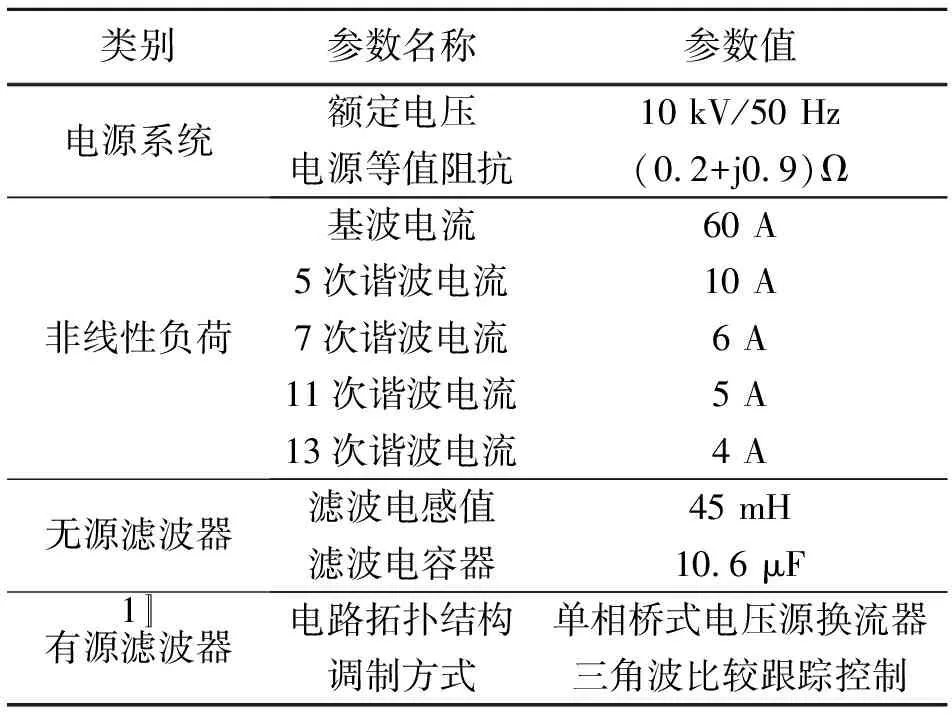
表2 系统仿真参数

图4为ATHPF补偿前后的电源电流波形，其中ATHPF采用了本研究所提出的控制策略来对系统中的5、7、11和13次谐波同时进行补偿。由图4可知，采用本研究所提出的控制策略可以实现ATHPF对系统谐波电流的良好滤波，补偿后的电源电流波形接近于一正弦波。

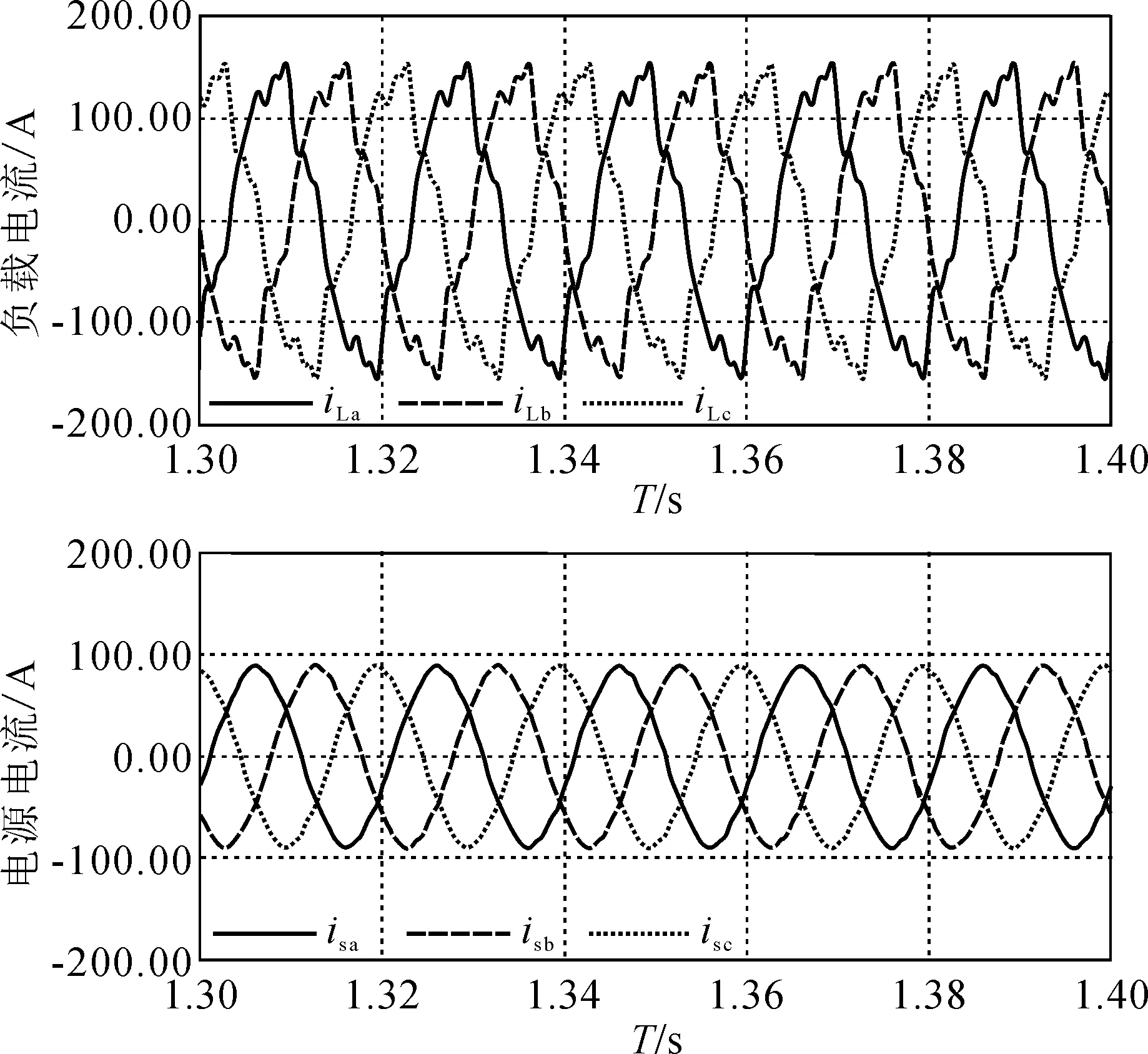
图4 系统仿真结果

3.2 实验结果分析

建立了单相ATHPF实验平台，其中，无源支路的LC参数按照3次偏调谐设计，滤波电感15.4 mH，滤波电容75 μF。有源装置APF采用两电平电压源换流器结构和三角波比较的PWM控制方式。谐波源负荷为带阻感负载的二极管整流桥。控制系统采用了本文所提出的改进无差拍控制策略，且有源调谐于5次和7次谐波。负荷电流也即未投入ATHPF时的电源电流波形及其频谱如图5所示。图6为投入ATHPF后的电源电流波形及其频谱图。

表3列出HIOKI3166电力分析仪测试所得的不同工况下电源电流的各次谐波电流幅值。

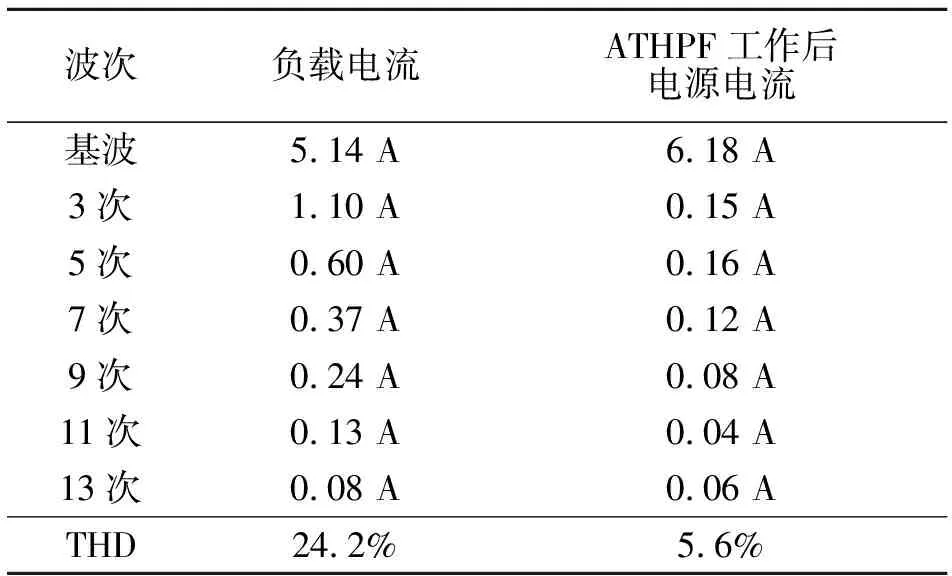
表3 电源电流谐波含量

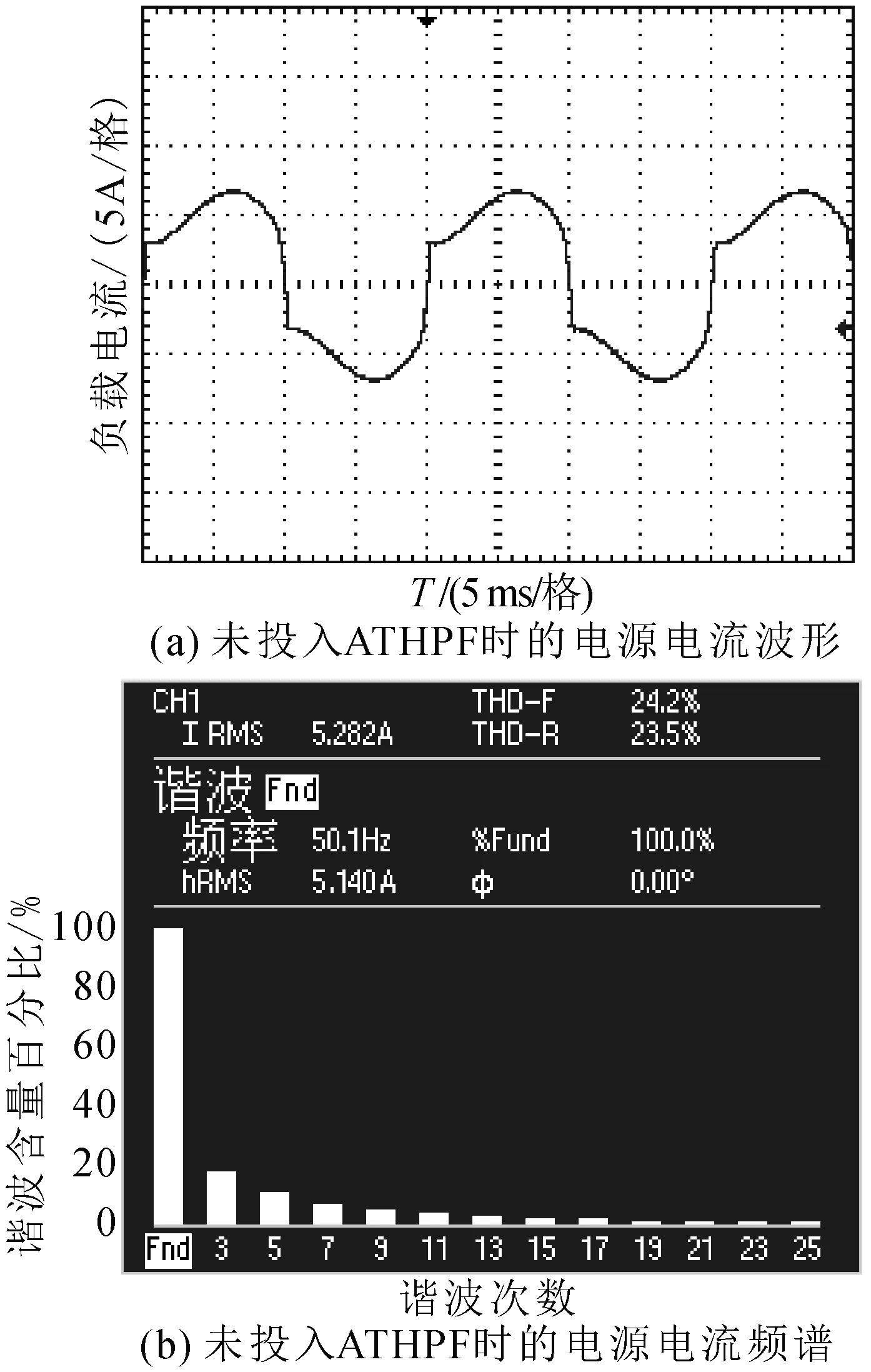
图5 未投入ATHPF时的电源电流波形及其频谱

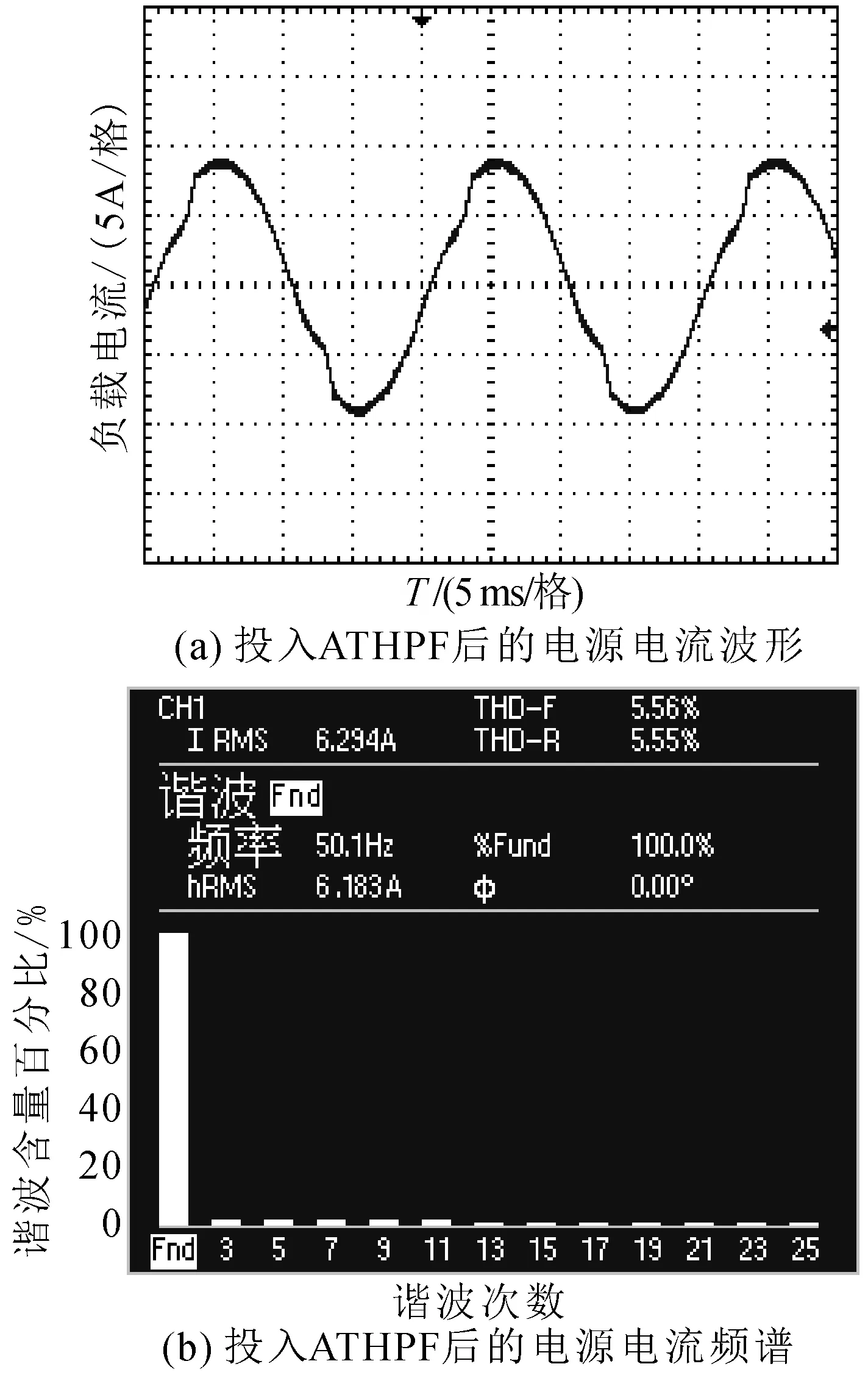
图6 投入ATHPF后的电源电流波形及其频谱

结合图5、图6及表3的数据可知，当滤波系统未投入运行时负载中的谐波电流全部都注入到了电网中，电源电流波形畸变较为严重，总畸变率高达24.2%，3、5、7次谐波电流含量分别为21.4%、11.7%、7.2%。当ATHPF投入运行时电源电流波形接近于正弦波，畸变率减小到5.6%，3、5、7次谐波电流含量分别降低到了2.4%、2.6%、2.0%，ATHPF对5次和7次谐波均起到了较好的滤波效果。

4 结 论

1) 有源调谐型混合电力滤波器中原有PI控制策略的参数整定较为复杂，提出了一种根据当前实测失谐度和谐波补偿系数直接计算有源滤波器谐波补偿系数的改进无差拍控制策略。

2) 实验系统的实测结果表明，基于改进无差拍控制策略的有源调谐型混合滤波器运行稳定、补偿性能良好，而且不存在调节器整定参数。

参考文献:

[1] Hamadi A, Rahmani S, Al-Haddad K. Digital control of a shunt hybrid power filter adopting a nonlinear control approach[J]. IEEE Transaction on Industrial Informatic,2013,9(4): 2092-2104.

[2] 漆铭钧，罗 安，刘定国. 注入式有源滤波器工程应用的关键技术[J].电工技术学报,2009,24(3):195-202.

Qi Mingjun, Luo An, Liu Dingguo. Key techniques in project application of injection type active power filter[J]. Transaction on China Electrotechnical Society, 2009, 24(3): 195-202.

[3]余健明，冯亚民.含分布式电源的配电网可靠性评估方法研究[J].西安理工大学学报, 2013, 29(4): 450-454.

Yu Jianming，FengYamin. Reliability evaluation method of distribution system with distributed generators[J]. Journal of Xi'an University of Technology, 2013, 29(4): 450-454.

[4]Etemadi A H. Control and protection of multi-DER microgrids[D]. Ottawa: University of Toronto, 2012.

[5] Hasan K N B M, Rauma K, Luna A, et al. Harmonic compensation analysis in offshore wind power plants using hybrid filters[J]. IEEE Transaction on Industrial Application, 2014,50(3):2050-2060.

[6] Verma V, Singh B. Design and implementation of a current-controlled parallel hybrid power filter[J]. IEEE Transaction on Industrial Application,2009,45(5):1910-1917.

[7] Corasaniti V F, Barbieri M B, Arnera P L, et al. Hybrid power filter to enhance power quality in a medium-voltage distribution network[J]. IEEE Transaction on Industrial Electronics,2009,56(8):2885-2893.

[8] 同向前,伍文俊,任碧莹. 电压源换流器在电力系统中的应用[M]. 北京:机械工业出版,2012.

[9] 邓亚平,同向前. 一种高压混合滤波器的两种控制方法比较[J].电力电子技术,2013,47(9): 43-45.

Deng Yaping, Tong Xiangqian. Compensation between two control methods for a hybrid power filter in high voltage application[J]. Power Electronics, 2013, 47(9): 43-45.

[10] 邓亚平，同向前，赵小利.有源调谐型混合滤波器的稳定性分析[J].电力电子技术,2013,28(4): 100-102.

Deng Yaping, Tong Xiangqian, Zhao Xiaoli. Stability analysis of active tuned hybrid power filter[J]. Power Electronics, 2013, 28 (4): 100-102.