多重分形及其改进算法研究
郭鹏程,孙龙刚,李辉,袁江霞
(西安理工大学 水利水电学院,陕西 西安 710048)
分形一词来源于拉丁文Fractus,是用来描述非常不规则以至不能视为经典几何研究对象的物体。
对分形集一般基于它的属性来定义,具有精细、不规则、自相似、递归的性质[1]。一般情况下,具有分形特征的图形,其分形维数高于其拓扑维数。
分形理论在包括信号处理在内的许多领域都得到了广泛的应用。研究过程发现,旋转机械的振动信号是一种典型的分形信号[2],因此可将分形理论应用到旋转机械故障诊断中来。
单一维数由于对盒子尺度的大小依赖性较强,对信号的局部特征描述性不够,而多重分形可以有效的弥补这一问题。
在用分形维数对分形体的分类研究中,出现这样的现象:具有不同纹理表面的两个分形体可能有相近或相同的分形维数。
基于这一事实,在如何提高这一领域的分形几何的算法方面人们做了大量工作。Evertsz和Mandelbrot于1992年提出,在描述一个分形集的几何特性方面,多重分形维数可能是一个比分形维数更合适的参数[3]。对于多重分形的研究表明,多重分形是一个比分形维数(盒维数)更适用的参数。文献[4] 基于数学形态学的分维数计算方法,采用形态学操作计算分形维数,提出了一种快速有效判断滚动轴承故障状态的新方法,对比分析结果表明该方法计算速度快,计算结果准确稳定。文献[5] 将多重分形方法应用于故障信号诊断中,并进行了实例测试和分析,证明了该方法在实际应用中的可行性;文献[6] 提出了广义维数最小二乘法的计算公式,并对转子系统实测时域故障信号进行了广义维数计算,结果显示各分形维数能较好地诊断和识别故障状态。文献[7] 采用基于多分辨率分析的小波系数去噪方法,通过在频域上对各层的小波分解系数的畸变量进行抑制以实现信号去噪,并通过试验验证了算法的有效性。文献[8] 提出了一种改进的多重分形维数算法,改变了传统多重分形维数对q维特征进行累加的计算方法,在保证算法计算复杂度基本不变的情况下增加了信号特征的规律性和类内聚集度。
本文介绍了基本的多重分形维数的计算方法,研究了影响其计算准确性的因素,发现在实际的计算中,除了盒子的尺度,盒子不同的运动方向也会导致多重分形维数的不稳定性。针对此问题,本文展开了有关的研究,提出一种改进的多重分形算法并进行了仿真计算。
1 盒子覆盖法
标准的盒子计算方法一般用来分析点集,每一组点集用广义维数或多重分形维数来描述。
广义维数通过改变一系列的值来定义函数进行计算,然后通过变换计算。
盒子计算法在1989年被提出,由Vicsek在1990年完善了其应用。其计算方法如下。
数学上,多重分形是根据其具有的分区功能来定义的:把所研究的对象分为N个小区域,分形体生长界面在第i个区域的生长概率为Pi(ε),以盒维数计算为基础,当盒子尺寸为ε时,定义Si(ε)为第i个小盒子内所有像素点灰度的数值之和,则第i个小盒子的平均灰度值可表示为:
(1)

不同的小区域生长的概率不同,用不同的标度指数αi表示。
(2)
在多重分形中,αi用来表示分形体小区域的分维,因为这些小区域数目趋于无穷,因此可以用f(αi)表示这个由不同αi组成的无穷序列构成的谱。f(α)和α是描述多重分形的一组参数。f(α)又被称为奇异谱。由于直接计算f(αi)和αi比较困难,因此一般选用另一组参数D(q)和q来描述。
首先定义一个配分函数Xq(ε),对概率Pi(ε)用q次方进行加权求和:
(3)
式中q为权重因子,τ(q)为质量指数,其表达式为:
(4)
定义q次信息维D(q)为:
(5)
两套参数α,f(α)和q,D(q)之间可以用Legendre法则进行变换:
(6)
或:
f(α)=qα-τ(q)
(7)
其中:
τ(q)=(q-1)D(q)
(8)
由式(6)可知,若已知α与其谱f(α),即可求出D(q)。反之,若测得Pi可得出D(q)。
式(8)两边同时对q求导,得:
(9)
根据式(7)可求出f(α)。
这种方法的优点是盒子一般在结构的中心,因此,即使有的盒子包含的信息很少,也不会溢出边界,当q<0时,包含信息少的盒子对结果也有很大的贡献。
盒子覆盖方法能够解决边界问题,当q<0时,允许重构多重分形谱,在计算时,需要二进制图像。运用小波模极大值计算有一定的限制,虽然其在选择尺度方面有一定的自由度,但计算比盒子覆盖法难以实现。
因此,本文在编制程序过程中,选用盒子覆盖法进行计算。
2 多重分形维数值的影响因素及其改进算法
2.1 尺度ε的取值
如上所述,选用盒子覆盖法计算多重分形谱,在计算过程中主要考虑计算概率测度时的盒子大小ε和配分函数中的q。
由式(1)可知,概率测度的大小取决于盒子大小ε,即ε的变化是影响Pi(ε)的主要因素。
概率测度基础是盒维数,其计算的思想与盒维数类似:用直径为ε的正方形盒子去覆盖一个分形体(信号),选择不同的ε会得到一系列的Si(ε),两者之间用式(10)表示的线性关系就是盒维数。
(10)
式中,D表示盒维数。
由上式可知,在盒维数的计算过程中,影响其结果的因素主要是盒子大小ε和Si(ε),而ε的大小决定Si(ε)的大小。这与多重分形中计算概率测度的性质一样。
在一般的盒维数计算中,一般只根据ε大小与Si(ε)的关系,并对一系列ε和Si(ε)线性关系进行判别,在实际的应用中笔者发现,即使对同一个分形体,在ε大小相同的情况下,得到的Si(ε)也可能是不同的。
如图1所示,盒子初始的位置左右相反,由相同的ε得出的Si(ε)分别是12和14。即在盒子的直径和分形体相同的情况下,由于盒子移动的初始位置不同,覆盖分形体所需要的盒子总数Si(ε)也是不同的。
因此,盒维数的计算结果也取决于盒子的相对位置,这个是多重分形谱计算过程中同样需要考虑的。

图1 相同的ε对应不同的Si(ε)
针对此问题,本文采用如图2所示算法流程,首先计算盒维数,在盒子ε变化的情况下,同时考虑盒子位置的变化,定义1~12个初始位置,分别计算其盒维数。
对得到的数值进行平均,最终以得出的均值维数作为实际的结果。

图2 算法流程
2.2 权重因子q的选择
基于统计物理方法计算的多重分形谱的配分函数Xq(ε)可以表示为式(3)形式。由式(3)可知,q值的不同表征了不同子集在配分函数中的重要作用。若q→+∞,则最大概率起决定作用,此时Xq(ε)反映了概率最大的子集的性质;相反地,若q→-∞,则表明最小概率起决定作用,即Xq(ε)反映了概率最小的子集的有关性质。多重分形就是以不同的q值作为边界对象,从而将分形体分成具有不同层次的区域来研究。
在理论上,q取值越大越好(-∞ 图3(a)和(b)分别画出了生成元为0.4/0/0.6和0.498/0/0.502的Cantor集的多重分型谱,图中的实线和点分别表示解析法计算的f(α)曲线和配分函数得出的f(α)曲线,标注为相应的q值。由图可以看出,随着|q|的增加,α和f(α)的值逐渐接近理论极限值。 图3(c)和(d)分别画出了0.4/0/0.6的Cantor集和0.2/0.6/0.2的Cantor集的α随q的变化,可见随着|q|增大到一定程度时,α基本上不再随|q|的增加而变化。 图3 Cantor集的多重分形谱 分形理论基于自相似原理,在任何标度下系统局部均相似于整体,这里的标度表示广义上的尺度。然而对于实际的情况,这一相似特性不可能在任何区间都成立,而只能在某一特定的区间内成立,即所谓的无标度区间。 2.3.1 相空间重构 实现自动确定的第一步就是由观测序列生成m维向量集合,该过程称为相空间重构。此时m表示嵌入维数。 由嵌入定理可知,若嵌入维数m≥2D+1,那么在重构空间Rm中系统结构同构于原空间。具体实现过程如下:假设已获得某一原始的观测序列{xi,i=1,2,…,N},选取合适的嵌入维数m和时间延迟τ进行相空间重构,将会得到空间中的一个点集Jm,该点集中的元素表示为: Xi=[xi,xi+k,xi+2k, …,xi+(m-1)k] i=1,2,…,Nm (11) 式中,Nm=N-(m-1)τ,为点集Jm中向量的个数;k是时间延迟数,若Δt为采样间隔,则τ=k·Δt,对离散时间序列而言,k也就是尺度r。 2.3.2 无标度区间的自动选择 从点集Jm中任选一个任意元素Xi,然后计算Xi到其余的Nm-1个元素的欧式距离,表示为: (12) 对所有的Xi重复这一过程,其中,当j=i时,rij=0。然后在相空间中计算q次关联积分,由于式(13)无法直接计算,重新定义q次关联积分如下: (13) 式中,H(r-rij)是Heaviside阶跃函数,并且有如下关系: (14) 当嵌入维数m足够大时,可以用q次关联积分得到广义分形维数Dq。 (15) 在各种尺度ε下按式(13)计算可得到Xq(ε),在对数坐标中做一元线性回归分析,拟合lnXq(ε)~lnε,所得直线的斜率即为广义分形维数Dq。 在实际计算中,标度ε满足的最大范围应该在两点间距的最小值与最大值之间,即: min{‖Xi-Xj‖}≤ε≤max{‖Xi-Xj‖} i,j∈Nm,且i≠j (16) 当标度ε较小时,关联积分Xq(ε)趋于零并且与后面的关联积分值有较低的线性相关程度,这样的ε值应该舍去;反之,如果标度ε很大,关联积分Xq(ε)将会达到饱和,会超出无标度区间的最大范围,这样的ε值也应该舍去。 使关联积分Xq(ε)的值饱和或者接近于零的ε值称为野值。 记Un=PilnPi,舍掉使NUM小于2的所有ε值。NUM表达式如下: (17) 具体算法流程如图4所示。 图4 无标度区间算法流程图 从图4可看出,确定无标度区间的基本过程如下:首先进行q次关联积分的计算,以q是否为1为界,若q=1,则直接进行关联积分的计算并确定尺度ε的取值范围,而当q≠1时,按照给定的尺度范围计算出中间变量,随后两种情况均对野值进行剔除操作,寻找相应区间的上下限或计算出相关系数,最终确定无标度区间的精确范围。 为了验证改进多重分形算法的有效性,本文选用Weierstrass函数进行验证仿真分析。 Weierstrass函数是数学上一个非常重要的函数,该函数具有处处连续但处处不可微的性质,是德国科学家Karl Weierstrass在1872年正式创造发表的。该函数的数学表达式为: (18) 式中,0<α<1,λ>1。 Weierstrass函数具有分形性质,任何局部的任意放大都与整体相似。其在数学上有严格意义上的分形盒维数,数学上对其证明的结果为: DB=2-α (19) 设a=λ-α=0.5,b=λ=3时,则函数可表达为: (20) 这里的盒维数理论值为: DB=2-α=2-0.631=1.369 在多重分形计算中,广义维数谱中D0即为盒维数。 图5为上式Weierstrass函数的曲线,选定参数如下:盒子尺度ε∈[1,45],权重因子q∈[-20,20],运用初始不考虑其盒子的相对位置算法得出的维数值D0=1.209 7。对其用改进的多重分形方法进行计算,初始参数不变,设定盒子的初始位置为4个。图6给出了维数计算的结果。表1为改进前后两种算法计算结果对比。 图5 Weierstrass 函数曲线 图6 广义维数谱 表1 结果对比 从表1可看出,用改进后的方法计算得到的结果其准确性更高。但是估计值始终与理论值存在差异,原因是盒维数实际上是点集(lnε, lnN(ε))的斜率,而拟合直线始终会存在着斜距。 本文对多重分形维数的计算方法作了基本介绍,并对影响其计算的因素-盒子尺度 和权重因子 进行了研究和分析。研究发现,除了盒子尺度 ,盒子的运动方向也对结果影响明显。因而,在编制计算程序时,加入了此影响因素并对算法进行了改进。实例结果表明:考虑盒子的相对位置得到的分形维数值更为准确和稳定。 参考文献: [1] Maragos P, Sun F K. Measuring the fractal dimension of signals morphological covers and iterative optimization [J]. IEEE Transactions on Signal Processing, 1993,41(1):108-121. [2] 徐玉秀, 钟建军, 刘薇, 等. 基于广义分形的旋转机械 故障诊断识别与分类[J].辽宁工程技术大学学报, 2005, 24(4):591-594. Xu Yuxiu, Zhong Jianjun, Liu Wei, et al. Application of multifactal theory to couping fault diagnosis[J]. Journal of Liaoning Technixal University, 2005, 24(4):591-594. [3] Jelinek H, Karperien A, Cornforth D, et al. Micromod - an l-systems approach to neural modelling[C]// Sixth Australia-Japan joint workshop on intelligent and evolutionary systems. Canberra, Australia, 2002. [4] 李兵, 张培林, 任国全, 等, 基于数学形态学的分形维数计算及在轴承故障诊断中的应用 [J]. 振动与冲击, 2010, 29(5): 191-194. Li bing, Zhang Peilin, Ren Guoquan, et al. Calculation of the fractal dimension based on mathematical morphology and application in bearing fault diagnosis[J]. Journal of Vibrarion and Shock, 2010, 29(5): 191-194. [5] Chunsheng E, Jiang Dongxiang, Ni Weidou. Fractal geometry and its applications in vibration failure symptom abstraction of the steam turbine [J]. Turbine Technology,1999,41(6):321-324. [6] 徐玉秀, 钟建军, 闻邦椿. 旋转机械动态特性的分形特征及故障诊断[J]. 机械工程学报, 2005, 41(12): 186-189. Xu Yuxiu, Zhong Jianjun, Wen Bangchun. Fractal fault diagnosis and classification to modal characteristic of rotor system[J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 186-189. [7] 王振朝, 岳莹昭, 师洁, 等. 基于多分辨率分析的小波系数压扩去噪算法[J].中国电机工程学报, 2008, 28(10): 76-81. Wang Zhenchao, Yue Yingzhao, Shi Jie, et al. Wavelet cofficients companding ce-noising algorithm based on multiresolution analysis[J]. Proceeding of the CSEE, 2008, 28(10): 76-81. [8] 宁宇. 一种简化的多重分形维数算法[J]. 价值工程, 2014, (9):181-182. Ning Yu. A simplified multi-fractal dimension algorithm[J]. Valve Engineering, 2014,(9):181-182.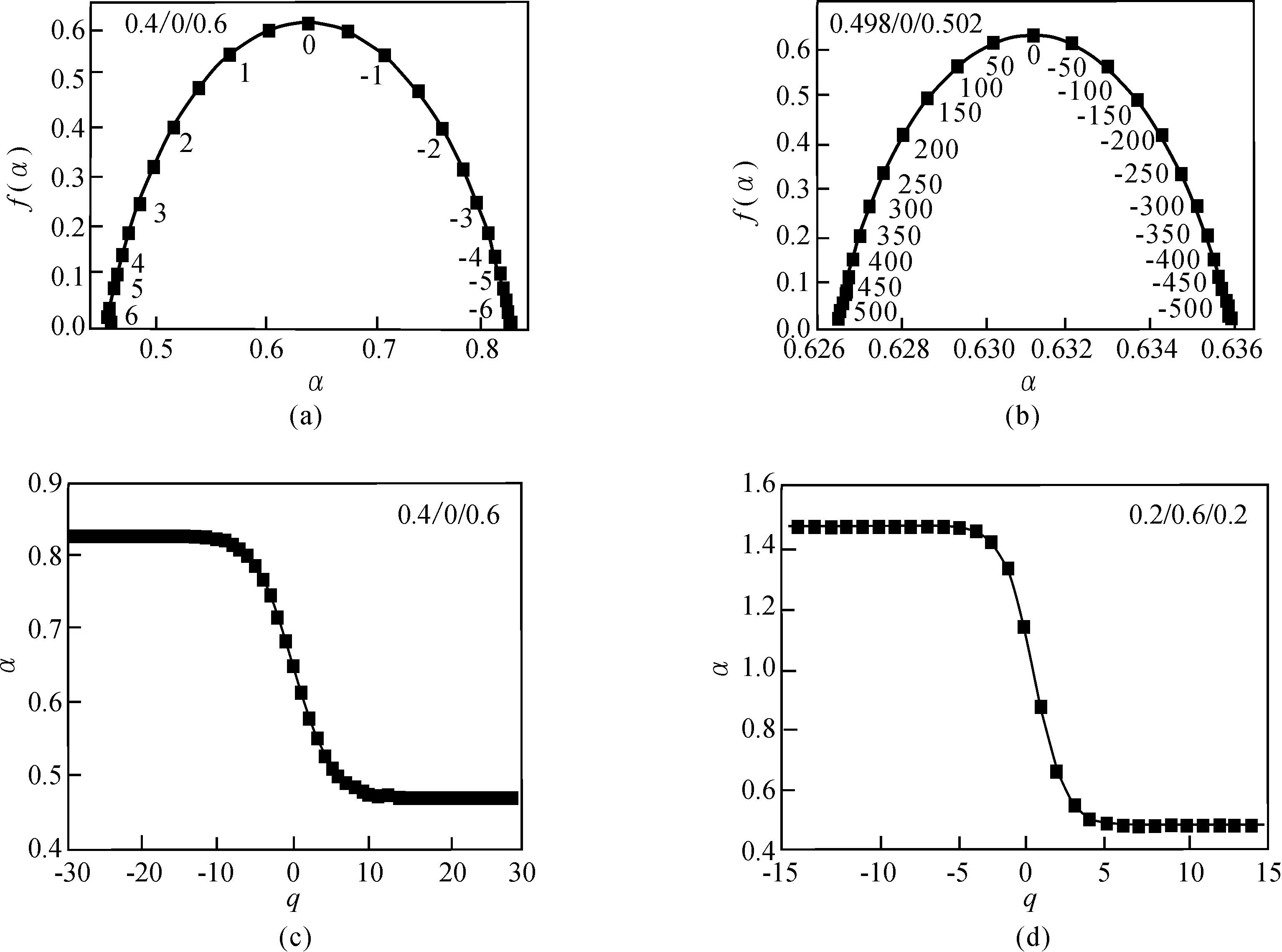
2.3 无标度区间的确定

3 仿真结果与分析



4 结 论

