基于PSO的无源电力滤波器支路拓扑的优化设计

姬军鹏，华志广，胡雪利，张静刚，曾光

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

随着电网中电力电子设备使用量的不断增加，负荷的非线性、冲击性和不平衡性对电网造成严重的谐波污染，所以谐波治理问题备受关注。

无源电力滤波器(PPF)以其结构简单、成本低、运行可靠性高等优势在中高压电网中仍得到了广泛应用。

目前，国内外对于PPF的研究，主要集中在滤波支路的参数优化设计方面，如文献[1]提出了一种基于PSO对混合滤波器中PPF参数进行优化的方法，该方法以初期投资成本、无功补偿容量和滤波效果为优化目标。文献[2]提出了一种改进PSO算法对PPF进行多目标优化，该方法实现了PPF参数的多目标优化。文献[3]提出一种基于随机权重的遗传算法求解PPF参数的方法，以谐波抑制、经济指标、无功功率补偿等为多目标综合优化了PPF参数。文献[4]提出了一种不影响收敛性的计算量很小的优化设计方法，该方法不是一味获得单一目标的最优，而是取得多限制目标的有效折中。

另外，还有一些文献对滤波支路补偿容量的分配方法进行研究，如文献[5]提出了一种以经济成本为目标的设计方法，该方法通过建立PPF多支路数学模型、以经济成本为目标对PPF的补偿容量进行优化设计。文献[6]对无功补偿容量的三种常用分配方法进行仿真及实际工况验证，给出特定工况下的最优分配方法。

上述方法虽然对PPF参数进行了有效的优化设计，解决了参数设计问题，但是均未涉及到PPF的支路拓扑优化方法，滤波拓扑的设计仍然依据工程经验来选择，其选型缺乏理论依据，没有在拓扑组合与PPF滤波效果、成本之间取得有效的折中。

本研究针对上述问题，提出了一种基于PSO的PPF支路拓扑的优化设计方法，该方法基于PSO优化了滤波网络中各支路的无功分配容量，以总投资成本最小、单调谐滤波支路平均品质因数最大及电流谐波平均含有率最小为目标优化出最佳PPF滤波支路网络，以充分优化PPF参数为基础，优化了滤波支路拓扑网络，是一个综合的、全面的优化设计方法。

本研究结合一个电力电网实例验证了所提出方法的正确性。该实例系统结构见图1。

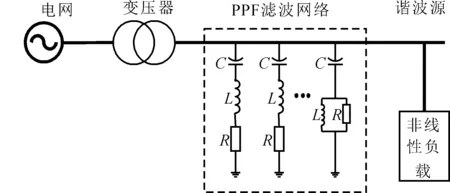
图1 工程实例系统主电路结构

图1工程实例系统中电网电压110 kV，最小短路容量6 000 MVA，X/R等于6。变压器容量63 MVA，变比为110 kV/10 kV。PPF滤波网络安装在变压器与非线性负载之间。非线性负载为三相可控整流桥装置，也是本工况的谐波源，产生6n±1(n为自然数)次的谐波电流。

1 PPF支路拓扑

PPF的支路拓扑结构可分为两大类，即调谐滤波器(Tuned Filter，TF)和高通滤波器(High Pass Filter, HPF)。

1.1 调谐滤波器支路拓扑

调谐滤波器包括单调谐滤波器(Single Tuned Filter，STF)和双调谐滤波器(Double Tuned Filter，DTF)，其拓扑结构见图2，应用最广泛的是STF，它利用串联电感和电容在某一频次产生串联谐振，使得滤波器在该频次呈现低阻抗特性，从而滤除该频次谐波。其阻抗频率特性曲线如图3所示[3,6]。

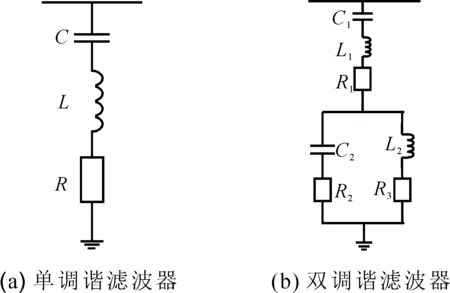
图2 调谐滤波器拓扑结构

图3 单调谐滤波器的阻抗频率特性

1.2 高通滤波器支路拓扑

高通滤波器包括一阶HPF、二阶HPF、三阶HPF及C型HPF，其拓扑结构见图4，其中二阶HPF应用最为广泛。HPF在谐波频次高于转折频率时，会呈现低阻抗特性，能够滤除高于转折频次的高次谐波。二阶HPF阻抗频率特性曲线如图5所示[6]。

图4 高通滤波器拓扑结构

图5 二阶高通滤波器的阻抗频率特性

2 PPF支路拓扑的参数优化

基于PSO对各种无源滤波支路拓扑组合进行参数优化，综合考虑了滤波器的支路投资成本、无功补偿容量和滤波效果参数指标，最终得到各拓扑组合支路的最佳补偿容量分配。

2.1 粒子群优化算法

PSO算法的基本思想是随机的初始化一群没有体积、质量的粒子，将每个粒子视为优化问题的一个可行解，粒子的好坏由一个事先设定的适应度函数来确定。每个粒子将在可行解空间中运动，并由一个速度变量决定其方向和距离。通常粒子将追随当前的最优粒子，并经逐代搜索，最后得到最优解。在每代中粒子将跟踪两个极值，一个是粒子本身当前找到的最优解，另一个是整个群体当前找到的最优解[7-9]。

假设有N个粒子组成的D维的群体，粒子i的位置为Xi=(xi1,xi2,…,xiD)T,粒子的速度为Vi=(vi1,vi2,…,viD)T, 个体极值表示为Pi=(pi1,pi2,…,piD)T，看作是粒子自身的飞行经验。全局极值为Pg=(pg1,pg2,…,pgD)T，看作是群体经验[10-11]。粒子通过自身经验和群体经验来决定下一步的运动。粒子在k+1代时，其位置更新公式为：

(1)

(2)

式中，i=1,2,…,N,N为群体中粒子的总数；d=1,2,…,D,D为自变量的个数；c1、c2为学习因子，通常取c1=c2=2，分别是调节向pbest(个体极值)和gbest(全局极值)方向飞行的最大步长；r1、r2为均匀地分布在(0,1)之间的随机数；xid∈(xdmin,xdmax)，vid∈(vdmin,vdmax)，(vdmin,vdmax)中的最大速度vmax决定了问题空间搜索的力度，粒子的每一维速度vid都会被限制在[xdmin,xdmax]之间，通常vdmax=k·xdmax，0.1≤k≤0.2。w为惯性权重，其大小决定了粒子对当前速度继承的多少，较大的惯性权重有利于全局寻优，较小的惯性权重则有利于局部寻优。

如果采用传统的单一线性化自适应调整w的策略，则一方面找到的最优值不稳定，容易陷入局部解，另一方面即使能够跳出局部解，其速度也非常缓慢。为了保证全局最优化，本研究采用分段调整w的策略。假设将粒子分为n段，每段的调整公式为[11-12]：

(3)

式中，t0和t2分别为该阶段的迭代初始值和迭代终止值；wl、wh为t0和t2代对应的w值。当分2段调整时，在1阶段通常取w=1.4～0.7，在2阶段取w=0.6～0.1。

2.2 目标函数、约束条件及适应度函数

2.2.1 目标函数

利用PSO对PPF支路拓扑组合网络参数的优化，实质上是对各个滤波支路无功补偿容量分配的优化，无功补偿容量以电容值大小体现，所以选取滤波支路中的电容值作为种群离子，用一组n维的向量来表示：Xi=[C1,C2,…,Cn]，其中n表示滤波支路的支路数。

选择支路投资成本和电压电流谐波畸变率两个参数作为优化目标函数。

1) 支路投资成本。无源滤波器的投资成本应最小，为简单起见，忽略了较小的附加成本，滤波支路初期成本计算式为：

(4)

其中，k1、k2、k3分别为无源滤波器的电阻、电感、电容所对应的价格因子(根据PPF元件的额定电压、额定电流来确定)；i为滤波器组的序号，n为滤波器支路组数。

2) 电压电流谐波畸变率。安装无源滤波器后，电网谐波含量应低于国家标准。系统的滤波效果以谐波电压、电流的总畸变率最小为衡量标准，谐波电压、电流的总畸变率公式见式(5)和(6)。

(5)

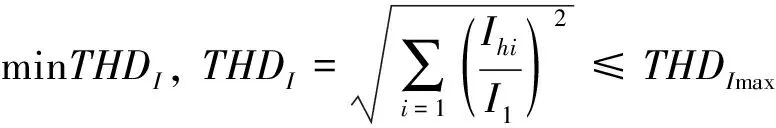
(6)

2.2.2 约束条件

PSO的约束条件为无功补偿容量。PPF的设计既不能出现无功功率过补偿，又要使系统的功率因数尽量接近1。即补偿容量应满足表达式为：

(7)

式中，Qmin、Qmax分别是PPF提供的基波无功功率的下限值和上限值。

2.2.3 适应度函数

根据目标函数和约束条件，建立各自的适应度函数。初期投资成本和电压电流谐波畸变率的适应度函数可表示为：

Y=minF(X)={F1(X),F2(X)}

(8)

F1(X)=F1

(9)

F2(X)=α1THDU+α2THDI

(10)

式中，α1、α2都是大于零的常数，用来匹配电压、电流的权重，一般取α1∶α2=1∶10。

2.3 基于PSO的参数优化设计

由于双调谐滤波器的安装和调试过程复杂,在实际工程中很少使用，且其成本等级与单支路调谐及高通滤波器不在同一等级，所以本研究对其不予考虑。由于滤波支路不同时优化设计效果无法参考对比，一般实际应用中以3条滤波支路应用最广[14]，所以本研究选择3条滤波支路作为优化条件。因此总共有53种拓扑组合网络。基于PSO的参数优化设计的流程图见图6所示。

初始化滤波支路电容值时，按照1.3倍经验值设置滤波电容最大值，按照0.7倍经验值设置滤波电容最小值，初始化电容值在最大值和最小值之间随机选取。

每个粒子的最大速度取变量的最大值，统一选取品质因数为60，每种组合均可以优化出一组最优值。

125种组合优化出的最优电容值见图7，其中3条单调谐拓扑组合的电容值C5为15.78 μF，C7为7.96 μF，C11为15.78 μF，由此计算出滤波器电感值L5为25.68 mH ，L7为25.97 mH，L11为25.68 mH。

图6 基于PSO的各支路参数优化设计流程框图

图7 125种组合优化后的电容值

3 PPF拓扑网络的优化设计

3.1 设计指标

对于不同种滤波器拓扑组合考察其总投资成本、单调谐滤波支路平均品质因数及电流谐波平均含有率三个指标。

1) 总投资成本指标

对于由三条滤波支路构成的53种拓扑组合网络，要找出总投资成本最小的拓扑组合网络。

2) 单调谐滤波支路平均品质因数

滤波器产生的功率损耗主要是电阻上的热损耗，电阻的大小由品质因数Q决定。对于高通滤波器，其阻抗与品质因数Q只有在转折频率处关系密切，在高频通带关系并不明显；而调谐滤波器的谐振点正是滤波频率点，因此，功率损耗指标可以转化为单调谐滤波器的品质因数Q指标。对各个滤波网路中的单调谐滤波器的品质因数Q取平均值，品质因数Q值越大，PPF功率损耗越小，滤波拓扑组合越好。

3) 电流谐波平均含有率

电流谐波含有率表示为：

(11)

其中，Ih为h次谐波电流值，I1为基波电流值。

这里提出谐波电流含有率用于考察各个滤波支路的滤波效果。基于仿真计算出滤波环境中各个谐波电流的含有率，并对其求平均值，谐波电流平均含有率最小的滤波拓扑组合最优。

3.2 优化设计方法及结果

PPF支路拓扑网络优化详细流程图见图8。

图8 PPF支路拓扑网络优化流程框图

基于总投资成本、单调谐滤波支路平均品质因数及电流谐波平均含有率三个指标，对53种PPF支路拓扑网络进行优化筛选。按照总投资成本指标消去70种高投资成本组合网络，按照单调谐滤波支路平均品质因数指标消去品质因数平均值最大的30种滤波网络组合网络，按照电流谐波平均含有率指标消去24种高电流谐波平均含有率组合网络，最终得到最优的1种PPF支路拓扑网络。其中，三种消去法的顺序可以随意变化，根据数据验证结果显示，三种消去法顺序的随意调整不会影响最优结果的产生。

通过这样的优化方法，得出3条单调谐滤波支路拓扑组合最优，滤波器具体参数见表1。表1同时也给出了根据工程实际经验得出的3条单调谐滤波器组合的参数值，以验证提出方法的优化效果。

表1 本研究提出方法优化设计的PPF滤波支路网络

4 实验结果及分析

安装滤波器之前，10 kV母线上的电压电流波形见图9。电压谐波状况见表2，电流谐波数据见表3。

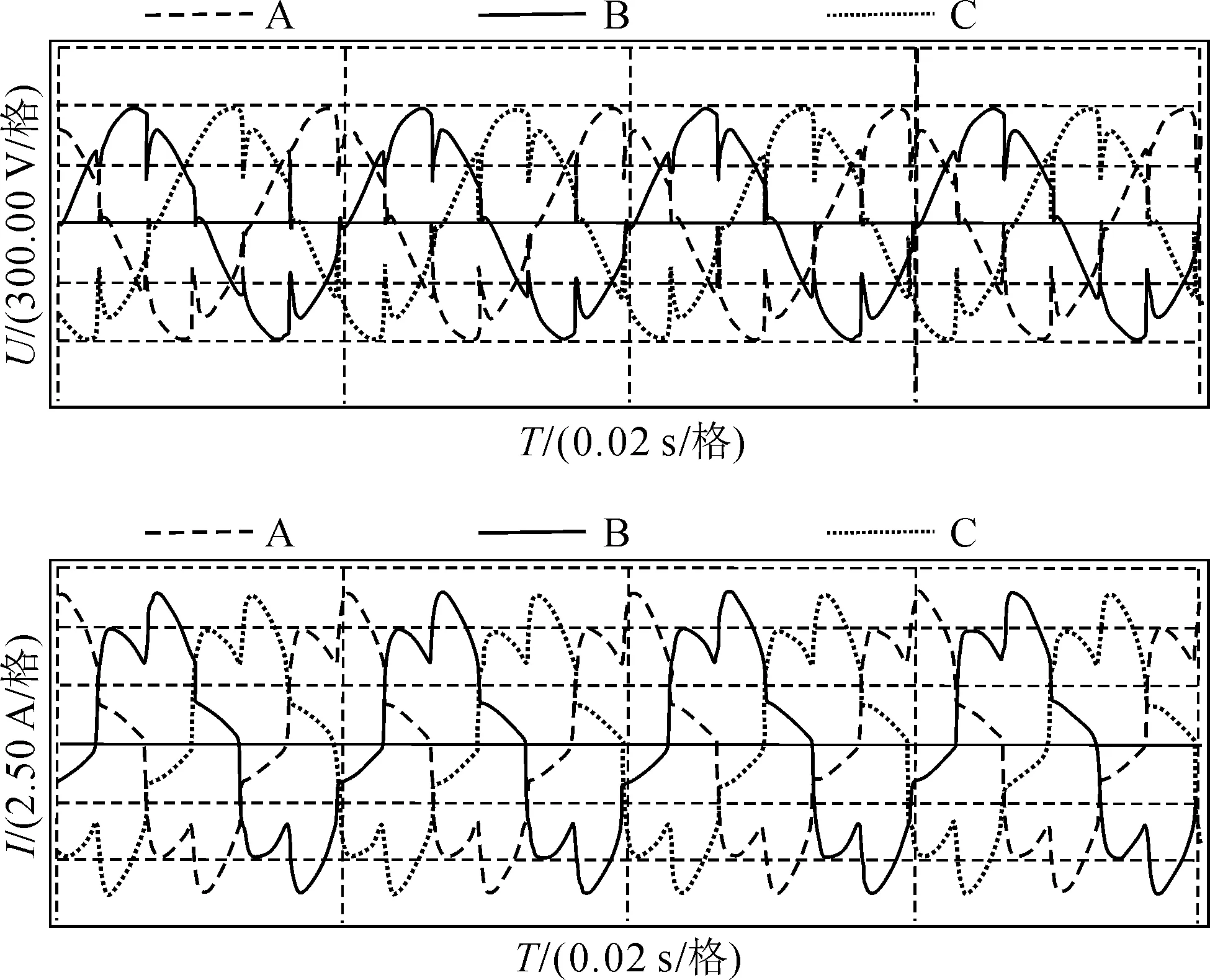
图9 滤波前10 kV母线的电压电流波形

工程经验选择的PPF滤波网络的滤波后电压电流波形见图10，电压谐波状况见表2，电流谐波数据见表3。

图10 工程经验PPF拓扑滤波后10 kV母线电压电流波形

本研究提出方法得到的PPF滤波网络滤波后的电压电流波形见图11，电压谐波状况见表2，电流谐波数据见表3。

图11 带有最优PPF拓扑的10 kV母线电压电流波形

从图9、图10、图11可以看出，本研究提出的方法优化的PPF支路拓扑明显优于根据传统经验设计的PPF支路拓扑。

从表2可以看出，本研究最优设计PPF在电压总畸变率、奇偶次谐波电压含有率比工程经验PPF明显小，完全达到国家标准。

从表3可以看出，本研究最优设计PPF在抑制各次谐波电流方面比工程经验PPF明显有优势，完全达到国家标准。

表2 滤波前后及国标电压谐波状况

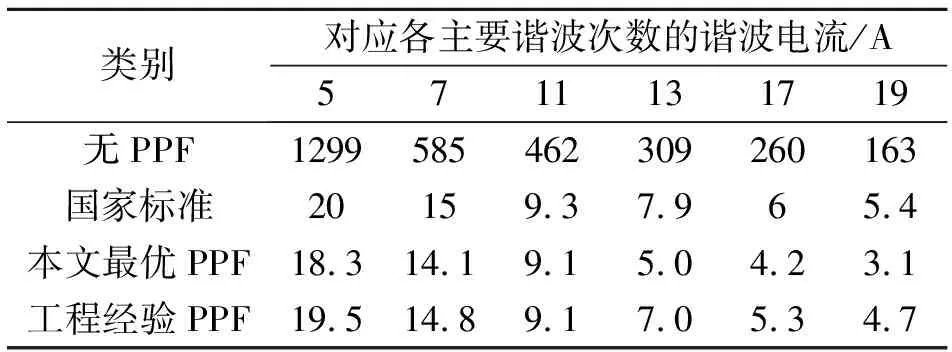
表3 滤波前后及国标电流谐波数据表

5 结 论

1) 本研究提出了基于PSO的无源电力滤波器支路拓扑的选择方法，可以给出某安装接点处安装PPF的最优拓扑结构及支路参数。

2) 该方法中滤波支路参数基于PSO对其进行优化，达到了支路投资成本最小、补偿容量合理、补偿效果满足国标的条件。该方法中滤波支路拓扑的优化，实现了总投资成本最小、功率损耗最小及滤波效果最好的目标。

3) 该方法的优化结果并不是在任何时候都是3条单调谐滤波支路网络最优，虽然不能给出一个适用于任何电力系统接入点的拓扑组合网络结论，但是给出了优化设计的方法与流程，给出了一种理论依据，在拓扑组合网络与PPF滤波效果、成本之间给出了优化设计，这对实际的工程设计过程很有帮助。

参考文献：

[1] 何娜, 黄丽娜, 武健, 等. 基于粒子群优化算法的混合有源滤波器中无源滤波器的多目标优化设计[J]. 中国电机工程学报, 2008, 28(27): 63-69.

He Na, Huang Lina, Wu Jian, et al. Multi-objective optimal design for passive part of hybrid active power filter based on particle swarm optimization[J]. Proceedings of the CSEE, 2008, 28(27): 63-69.

[2] 李永安, 李圣清, 罗晓东, 等. 混合有源电力滤波器中无源滤波器多目标优化设计[J]. 湖南工业大学学报, 2012, 26(1): 46-49.

Li Yongan, Li Shengqing, Luo Xiaodong, et al. Multi-objective optimal design for passive part of hybrid active power filter[J]. Journal of Hunan University of Technology, 2012, 26(1): 46-49.

[3] 魏伟, 许胜辉, 孙剑波. 一种无源滤波器的优化设计方法[J], 电力自动化设备, 2012, 32(1): 62-66.

Wei Wei, Xu Shenghui, Sun Jianbo. Optimal design of passive filter[J]. Electric Power Automation Equipment, 2012, 32(1): 62-66.

[4] Zobaa A F. Optimal multi-objective design of hybrid active power filters considering a distorted environment[J]. IEEE Trans. Industrial Electronics, 2013, 61(1): 107-114.

[5] Elmathana M T, Zobaa A F, Abdel Aleem S H E. Economical design of multiple-arm passive harmonic filters for an industrial firm-Case study：IEEE 15th international conference on harmonics and quality of power[C]. Hong Kong: IEEE, 2012: 438-444.

[6] 姬军鹏. SVC系统滤波器的设计及分析[D]. 西安: 西安理工大学, 2009.

Ji Junpeng. The design and analysis of SVC system filter[D]. Xi’an: Xi’an University of Technology, 2009.

[7] 黄磊. 粒子群优化算法综述[J]. 机械工程与自动化, 2010, (5): 197-199.

Huang Lei. Overview of particle swarm optimization[J]. Mechanical Engineering & Automation, 2010, (5): 197-199.

[8] Hashemi A B. A note on the learning automata based algorithms for adaptive parameter selection in PSO[J]. Applied Soft Computing Journal, 2011, 11(1): 689-705.

[9] Tsujimoto T, Shindo T, Kimura T, et al. A relationship between network topology and search performance of PSO：IEEE congress on evolutionary computation ,QLD: IEEE[C]. Brisbane, 2012: 1-6.

[10] Rakhshani E, Cantarellas A M, Remon D, et al. PSO-based LQR controller for multi modular converters: IEEE annual international on energy conversion congress and exhibition,VIC: IEEE[C]. Melbourne, 2013: 1023-1027.

[11] 余健明, 马小津, 倪峰, 等. 基于改进PSO-LSSVM的风电场短期功率预测[J]. 西安理工大学学报, 2013, 29(2): 176-181.

Yu Jianming, Ma Xiaojin, Ni Feng, et al. Short-term power forecasting of wind farm based on an improved PSO-LSSVM[J]. Journal of Xi’an University of Technology, 2013, 29(2): 176-181.

[12] Ling Haifeng, Xiao Yihong, Zhou Xianzhong, et al. An improved PSO algorithm for constrained multi-objective optimization problems:international conference on computer science and service system[C]. Nanjing China: IEEE, 2011: 3859-3863.

[13] Vazquez J C, Valdez F. Fuzzy logic for dynamic adaptation in PSO with multiple topologies:IFSA world congress and NAFIPS annual meeting, AB: IEEE[C]. Edmonton, 2013: 1197-1202.

[14] 陈静, 雷磊, 袁佑新, 等. 新型动态调谐无源滤波器的研制与应用[J]. 电工技术, 2013, (2): 3-13.

Chen Jing, Lei Lei, Yuan Youxin. et al Development and application of a new dynamic tuned passive filter[J]. Electric Engineering, 2013, (2): 3-13.