基于BP网络的锅炉炉膛温度测量算法
杨聚庆 , 刘娇月, 崔 鹏
(1. 河南工业职业技术学院, 河南 南阳 473009; 2. 河南红宇企业集团有限责任公司, 河南 郑州 451450)
炉膛火焰燃烧状况直接关系到锅炉运行的经济性,建立精度较高的炉膛温度场测量方法,得到炉膛内温度的实际分布,对判断燃烧状态的好坏是十分必要的,而温度场建立的最重要因素之一就是温度测量算法,设计高精度的温度测量算法,将直接影响锅炉运行的经济性。比色测温法在测量炉膛二维温度场实际中应用较多,但也存在很多问题,如误差较大、参数标定复杂、实验室黑体炉标定的结果与实际测量时差别较大等[1]。
人工神经网络是现代神经生物学和认识科学对人类信息处理研究的基础上提出的,具有很强的自适应性和学习能力、非线性映射能力、鲁棒性和容错能力。其中前馈型网络和反馈型网络是两种典型的结构模型。误差反向传播神经网络,即BP网络(back propagation)是一种单向传播的多层前向网络,在模式识别、图像处理、系统辨识、自适应控制和函数拟合等领域都有广泛的应用。其基本思想是最小二乘算法。它采用梯度搜索技术,以期使网络的实际输出值与期望输出值的误差均方值为最小。BP算法的学习过程由正向传播和反向传播组成。在正向传播过程中,输入信息从输入层经隐含层逐层处理,并传向输出层,每层神经元(节点)的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出,则转入反向传播,将误差信号沿原来的连接通路返回,通过修改各层神经元的权值,使误差信号最小[2-3]。
本文主要针对温度测量算法存在的诸多问题,将先进的BP神经网络用于测量温度算法,并采用Matlab软件对实验数据进行了处理和结果验证。实验结果表明温度场的测量精度得到较大提高。
1 温度场测量算法分析
CCD摄像机输出的数字图像某点的RGB分量的灰度值RR、RG、RB和该点的温度T存在非线性关系:
T=f(RR,RG,RB)
(1)
如果在理想情况下,只考虑RGB分量中的2个灰度值,该非线性关系的函数解析式可表达[4]为:
(2)
(3)
如果将RGB分量中的3个灰度值均考虑,该非线性关系的函数解析式可表达为
(4)
式中,λ为辐射电磁波波长,ε为辐射体的黑度系数,T为温度,K、V、、C2为辐射常数。
但如从实际出发,不考虑为计算温度而设立的众多假设,比方说将火焰视为黑体[5]等,则式(1)函数的解析表达式将是非常复杂,且有许多不确定系数,因此利用式(1)的解析形式来求解温度与灰度值RR、RG、RB的关系是非常困难的[6]。
BP神经网络具有自学习和逼近任意有界非线性函数的能力。所以可以利用BP神经网络来构造一个“黑箱”,并通过神经网络的自学习以逼近式(1)函数关系。考虑到所逼近函数的复杂性和神经网络输出是一温度值,因此可选用含有2个隐含层的4层BP神经网络来逼近温度与灰度值RR、RG、RB的函数关系,其网络输入为RGB分量的灰度值,输出层为一个神经元,表示测量温度。学习好的网络可代替式(1)用于计算温度[7-9]。
2 BP网络结构设计
神经网络的结构如图1所示,包括输入层、2个隐含层和输出层。

图1 神经网络结构
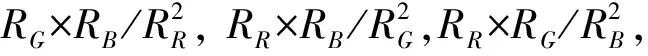
(2) 隐含层。有2个隐含层,隐含层的传递函数选择双曲正切函数,因为双曲正切函数可以使神经网络具有较好的收敛性能。一般情况下只需要选择1个隐含层,然后改变隐含层节点的个数即可,但如果对于较复杂的问题,可能需要大量的隐含节点和较长的训练时间,并且存在精度不够高的问题,所以在这里选择了2个隐含层的结构。对于具有2个隐含层的神经网络,在选取隐含层节点数目时,一般原则为:对靠近输入层或输出层的隐含层,其神经元个数应该为输入神经元个数或输出神经元个数的2~4倍[10],当然这只是一个基本的指导原则,具体的选择还是要通过实验来选,即在满足学习精度的前提下改变各隐含层的神经元个数以尽量减少神经网络学习次数,通过比较后选择。由于BP神经网络的收敛与初始权值的选择有关,需通过多次实验比较以选择合适的隐含层的神经元个数。从表2可以看出,网络结构为3-6-3-1、3-7-3-1、3-8-3-1和3-9-3-1时,在相同的训练误差下学习次数都较少,在这里选择了第1个隐含层有8个神经元,第2个隐含层有3个神经元的3-8-3-1结构作为测温网络。
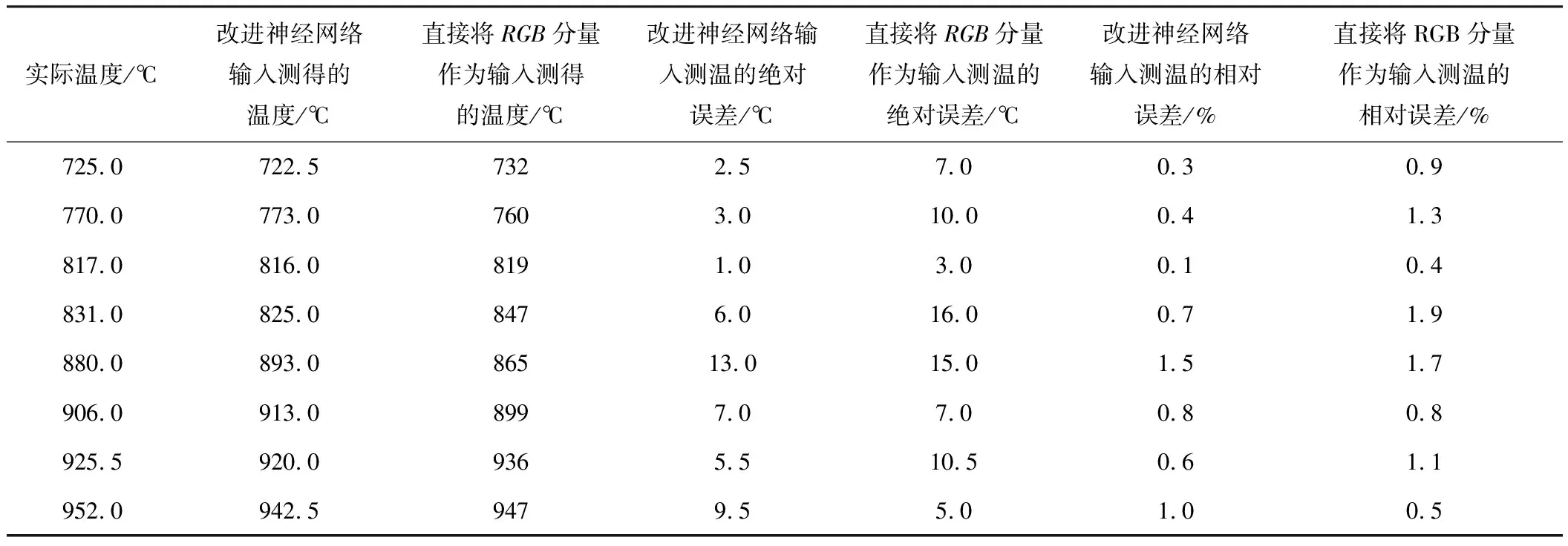
表1 不同神经网络输入层形式下测量结果

表2 不同神经元下网络的训练情况(err<0.005)
注:…表示不能收敛或训练次数大于20 000次仍未收敛。
(3) 输出层。仅有1个神经元,转移函数为一简单线性函数,这样神经元输出值能直接表示测量温度。
3 BP网络的学习训练
采用在高温电阻炉内进行实验可以获得训练样本。电阻炉具有升温快、炉温均匀性好等特点。实验用的电阻炉能达到1 100 ℃左右的高温,并配有温度控制器和热电偶测温装置,特别适合标定。将炉温控制在给定温度点后,利用CCD摄像头和图像采集卡采集炉内的图像,并传送到计算机作为神经网络训练用的样本。
在Matlab下开发用于处理图像样本的代码,将样本转换为可以输入到神经网络的形式,当在给定训练次数内如果网络收敛并且误差小于给定值就认为训练成功。
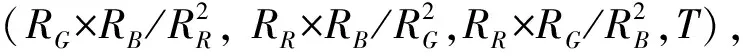

学习速率决定每一次循环训练中所产生的权值变化量。大的学习速率可能导致系统的不稳定,但小的学习速率导致较长的训练时间,可能收敛很慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于误差最小值。所以一般情况下倾向于选取较小的学习速率以保证系统的稳定性。学习速率的选取范围是0.01~0.8[12]。
另外为了加快训练速度,避免陷于局部最小和保证网络的稳定性,本文还采用了带动量因子算法,即网络权值调整公式中加入了动量因子。权值调整方式为
(5)

在设计网络的训练过程中,期望误差值也应当通过对比训练后确定一个合适的值,学习误差的定义:
(6)
式中p为学习样本个数,T为实测温度,y为网络输出温度值,当err<0.005时停止学习。从式(6)可以看出,由于温度值一般较大,从网络的实现角度考虑,将温度值除以100作为输出。误差小于0.005即最后温度误差在20 ℃以内。
4 实验结果
图2是结构为3-8-3-1的BP神经网络学习时的误差变化情况,可见网络的收敛速度较快。
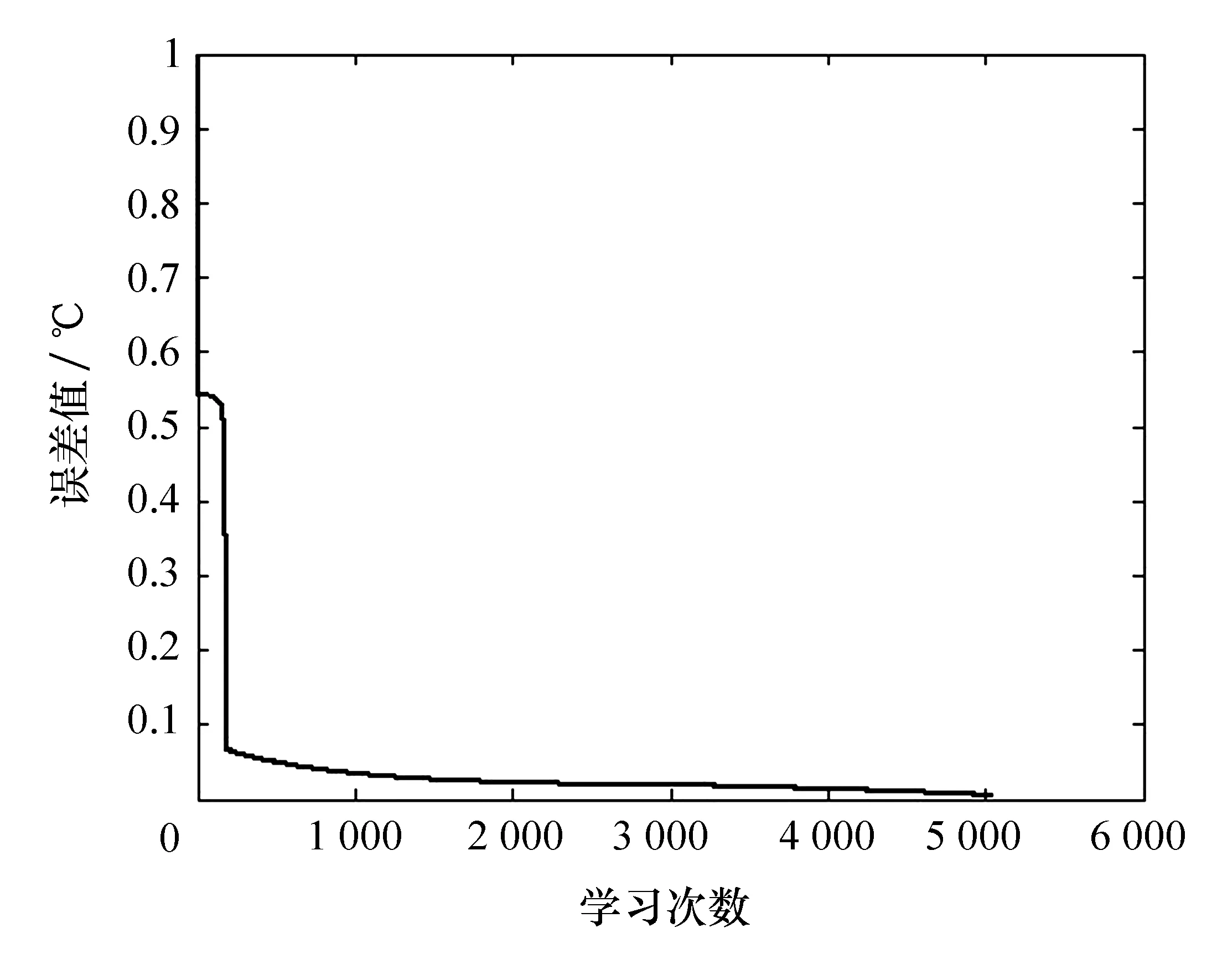
图2 误差曲线
将学习好的BP神经网络计算温度场,测试点温度为863 ℃时,神经网络计算温度为854 ℃。图3是当黑体炉测温度点为863 ℃时的黑体炉图像,图4是BP神经网络得到的二维等温线图。

图3 炉内图像

图4 炉内等温线
可以看出神经网络测温方法的准确性较高,最后将其应用于实际炉膛火焰温度的测量,图5为一幅火焰图像,图6为神经网络计算的燃烧二维温度场等温曲线。由以上测量结果以及图像比较可见,测量的温度场较好地反映了燃烧特征。

图5 火焰图像
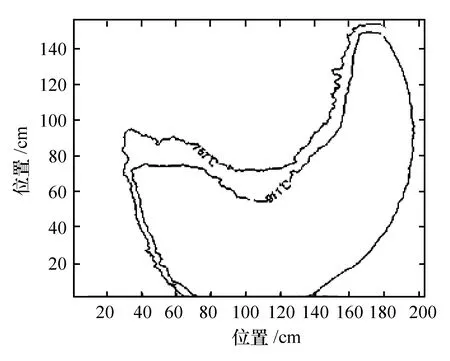
图6 火焰等温线
[1] 张玉杰,吕岑.基于彩色CCD锅炉火焰温度场测量方法研究[J].量子电子学报,2004,21(5):674-678.
[2] 施鸿宝.神经网络及其应用[M].西安:西安交通大学出版社,1993:20-47.
[3] 焦李成.神经网络计算[M].西安:西安电子科技大学出版社,1993:37-39.
[4] 张玉杰,吴平林,路昌明.基于数字图像处理和神经网络的炉膛温度场测量及燃烧诊断方法的研究[J].热力发电,2004(7):18-21.
[5] 高武. 锅炉火焰检测算法研究[D].南昌:南昌大学, 2008.
[6] Yang Juqing,Liu Jiaoyue. Design of Stepper Motor Controller Based on Fuzzy BP Neural Network[J]. Advanced Materials Research. 2012,479/4801/481:2630-2633.
[7] 刘耀东,陈祥宝.采用人工神经网络求解箱梁温度场算法研究[J].中国公路学报,2000,13(1):69-72.
[8] 张凤春,董增寿,刘明君.基于数字图像处理技术计算炉膛温度场方法研究[J].计算机与数字工程,2008(7):137-139.
[9] 谢刚,王理飞,谢克明.燃煤电站锅炉火嘴图像分割研究[J].太原理工大学学报,2006,37(5):521-523.
[10] 吴伟华,朱宝宇.丰城发电厂锅炉炉膛火焰检测改造工程[J].中国电力,2001,34(11):64-66.
[11] 黄本元,罗自学,周怀春.炉膛燃烧稳定性的火焰图像诊断方法[J].热力发电,2007(12):19-22.
[12] 陈志刚,蒙建波,李良熹.电站锅炉数字图像火焰检测系统设计与实现[J].重庆大学学报:自然科学版,2003,26(2):32-35.

