方波输入下LC电路暂态过程实验研究
刘洪臣, 陈 东, 刘 雷
(1. 哈尔滨工业大学 电气工程及自动化学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)
二阶电路的暂态过程分析是电路理论课程学习中非常重要的内容[1-5]。在RLC串联电路的暂态分析中,当RLC电路中原件参数满足一定的条件时,电路会出现过阻尼、欠阻尼及临界3种情态[4-7]。特别是在欠阻尼条件下,当电阻为零时会出现不衰减的自由振荡,即等幅振荡的情况[4,8]。在以往对串联LC电路进行分析的教学中,通常以零输入响应或直流输入为例,很少分析电容在换路时刻的初始值对输出的影响。在教学过程中,为了让学生深入理解LC串联电路的暂态过程,同时做到以点带面、从一个典型电路引申到一类电路,做到学有所用,避免死记硬背,本文对方波激励下的二阶LC电路的暂态过程进行了详细的分析。通过控制方波频率,使得电容和电感在换路时刻的初始值发生变化,分析状态变量的初始值对输出的影响,最后再进行仿真验证。由于Orcad/Pspice软件是电路分析中常用的软件,能够反映电路的实际情况[9-12],因此本文选择Orcad/Pspice软件进行实验验证。通过这种先理论分析再仿真验证的方式更能加深学生对二阶电路暂态过程的理解。
1 LC串联电路的暂态过程
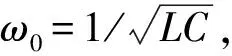

图1 LC串联电路
将Us一个周期内的表达式为:
(1)
在开关闭合后,根据基尔霍夫电压方程可以得到
(2)
初始条件为:
微分方程的特征方程为
(3)
解得特征根为
P1=jω0,P2=-jω0
方程的通解为
Uch=A1sin(ω0t)+A2cos(ω0t)=Asin(ω0t+θ)
特解为Ucp=U0,U0是Uc的稳态解。
得到
Uc=Uch+Ucp=Asin(ω0t+θ)+U0
代入初始条件A=-U0,θ=π/2后可以得到
(4)
在t=t0时电路进行换路,通过确定电容电压和电感电流此时的数值再进行下一步的分析。下面将通过控制方波的周期使得电容电压和电感电流在换路时刻的初始值发生变化,从而改变电容电压及电感电流。
2 不同周期方波激励下LC串联电路的暂态过程分析
2.1 方波周期为振荡周期的n倍(n为整数)
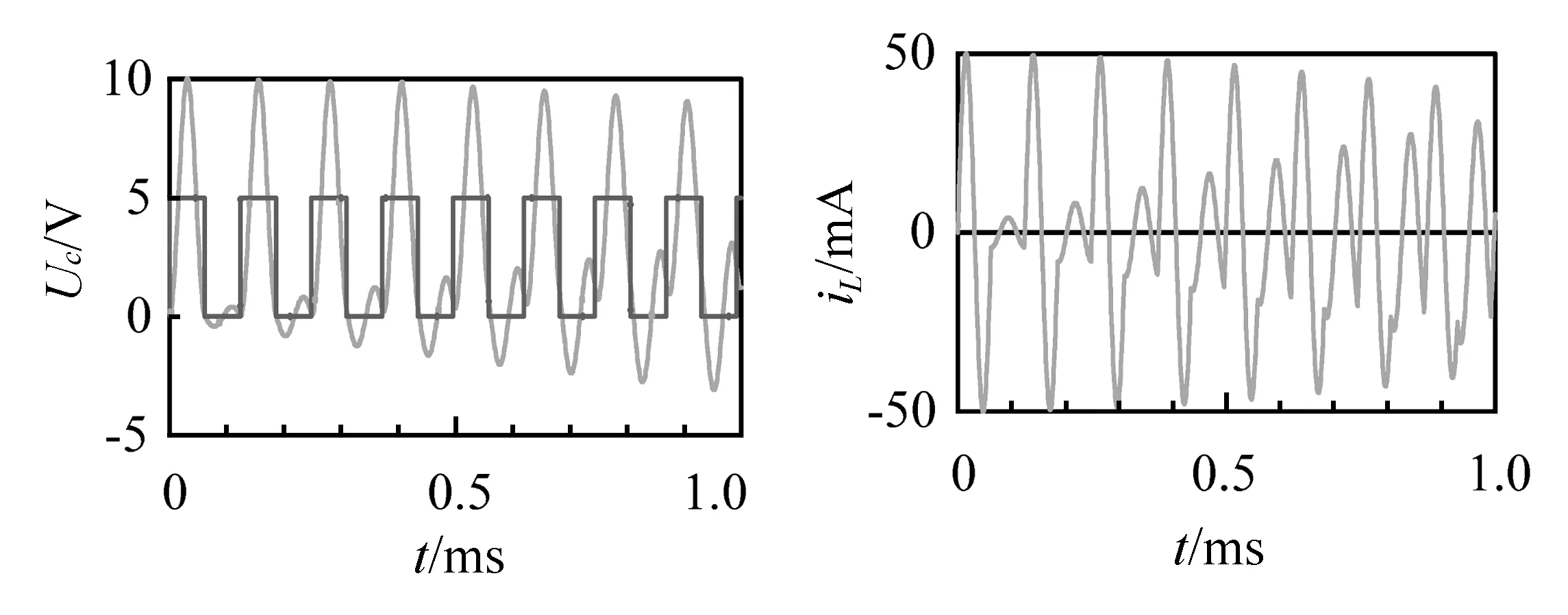
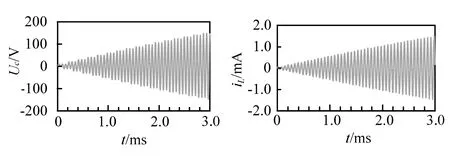
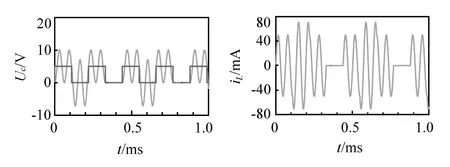
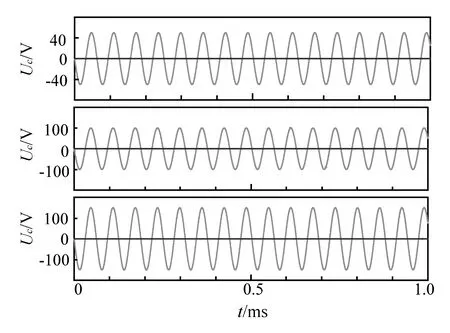
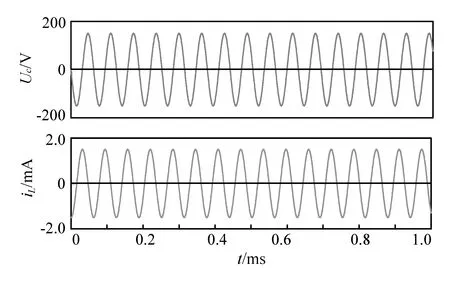
设置方波周期T′=2T,根据式(4),在t=0时刻,电容电压为0 V,激励源接通,通过对1个周期内Uc和iL的分析可以得知,当方波的高电平结束时,电容电压和电感电流的数值为零,即此时电路状态变量的初始值为零。当激励源进入低电平时,电路中激励与初始值均为零,因此在时间段0.5T′ T′=2T条件下的仿真结果如图2所示,与理论结果完全相同。T′=6T时的仿真结果如图3所示。结合图2和图3可知,只要合理地控制方波周期为振荡周期的整数倍,即Uc和iL在高电平结束的时刻数值为零,则可以使Uc和iL在高电平阶段呈等幅振荡,而在低电平阶段为零。 图2 T′=2T时,Uc和iL的波形 图3 T′=6T时,Uc和iL的波形 当方波周期为振荡周期的n+m倍(0 (5) 根据在低电平阶段为零输入响应有: (6) 代入初值条件t=0可以得到: (7) 解方程(7)组可以得到: (8) 在下一个高电平的起始处Uc和iL的值与此时的初值相等,且此阶段时的振幅较脉冲阶段减小,进入下一个脉冲时,为全响应,有: (9) 根据全响应可以得到: (10) 代入初值条件t=0可以得到: (11) 解得: sinθ=cos(ω0mT) (12) T′=(n+m)T时的仿真结果见图4(上图为放大图)。 图4 T′=(n+m)T(0 结合理论分析和仿真结果,电容在低电平期间为零输入响应,且在下一个脉冲开始时Uc和iL不为0,使得脉冲期间Uc的振荡幅度逐渐减小;低电平时Uc的振荡幅度逐渐增大,而且Uc相对于激励源逐渐左移,经历一定时间后,相位又和脉冲时间的相位大致相重合,振荡幅度重新达到最大值,然后再和以前一样再减小,呈周期性变化。 图5 T′=(n+1/4)T时Uc和iL的波形 此种情况的分析与2.2节情况相同,结果也非常类似,仿真结果如图6所示。 图6 T′=(n+m)T(1/4 根据前面的理论分析结果,再进入低电平时有: Uc0=2U0,iL=0 (13) 此时电路相当于是零输入响应,根据计算可以得到: (14) 由此可以得到再进入高电平时有: Uc0=-2U0,iL=0 (15) 根据此时为全响应,可以得到: (16) 由此推断,可以得知在第n个脉冲时有 A=(2n-1)U0 (17) 在第n个低电平阶段时,A=2nU0 电容电压会增加到正无穷,在实际应用电路当中应当尽量避免这种情况的出现,否则的话会损坏电路元件,发生危险。仿真结果如图7所示,和理论分析完全相符。 图7 T′=(n+1/2)T时Uc和iL的波形 此时分别与第2.2节和2.4节中情况类似,不同之处是两者波形移动的方向不同,仿真结果见图8和图9。 图8 T′=(n+m)T(1/2 图9 T′=(n+m)T(3/4 图10为仿真结果。 图10 T′=(n+3/4)T时Uc和iL的波形 图11中从上到下分别为电容初始电压为1、2、3 V时Uc的变化图,可见Uc峰值随初始值有变化,而且为等幅振荡,振荡周期与电源激励的周期无关。图12是Uc和iL的对比图。 图11 全响应 图12 全响应(Uc初始值为3 V)时Uc和iL 由图12中电压电流对比可以知道,由于电容初始电压不为零,导致在电路t=0时,电容可以等效为一个电压源,其电压和原有激励源的电压相反,两者相减得到了一个新的激励源,电压为(Us-3)V,而此时电感由于本身电阻很小,在电路里基本上相当于短路,因而电路中电感的初始电流很大,而且初始振荡电流和电容电压的初始值线性相关。 本文通过对方波输入下的串联LC电路展开分析,并通过Orcad/Pspice良好的仿真环境对理论分析进行验证,使学生对二阶电路暂态过程的仿真方法有所了解,并且通过这种先理论分析再仿真验证的方式加深学生对二阶电路暂态过程分析方法的理解。 [1] 周宦银,吕子勇,孟艳,等.二阶电路阶跃响应的计算机辅助教学研究[J].中国现代教育装备,2006(11):52-54. [2] 董圣英. Matlab在二阶电路动态分析中的应用[J].电气电子教学学报,2010,32(5):116-118. [3] 童立君,杨小芹,彭登峰.二阶电路过渡过程教学的研究与探讨[J].电气电子教学学报,2007,29(5):24-26. [4] 陈希有. 电路理论基础[M]. 北京:高等教育出版社,2004. [5] 周玉坤. 电路[M]. 北京:电子工业出版社,2005. [6] 朱勤. Pspice 仿真软件在LC 振荡器设计教学中的应用[J].实验技术与管理,2009,26(8): 80-84. [7] 李明,方波,陈素华,等. Pspice仿真二阶电路的零输入响应[J].科技信息, 2012(1):235-236. [8] 陈桂真, 石超, 刘晓文. 二阶电路中等幅振荡和增幅振荡的实现[J].实验技术与管理,2009,26(4):29-31. [9] 李永平. PSpice电路仿真程序设计[M]. 北京:国防工业出版社,2006. [10] 夏江涛, 肖韶荣, 孙冬娇.PSpice 在工科电类专业教学中的应用[J].实验技术与管理, 2010,27(12):121-124. [11] 曾爱明,王云亮.PSPICE在电力电子虚拟实验室中的应用[J].天津理工大学学报,2009,25(4):46-48. [12] 高燕梅, 王丽. 基于PSPICE的振荡器起振特性的仿真研究[J].实验技术与管理, 2007,24(2):91-93.

2.2 方波周期为振荡周期的n+m倍(0

2.3 方波周期为振荡周期的n+1/4倍
2.4 方波周期为振荡周期的n+m倍(1/4
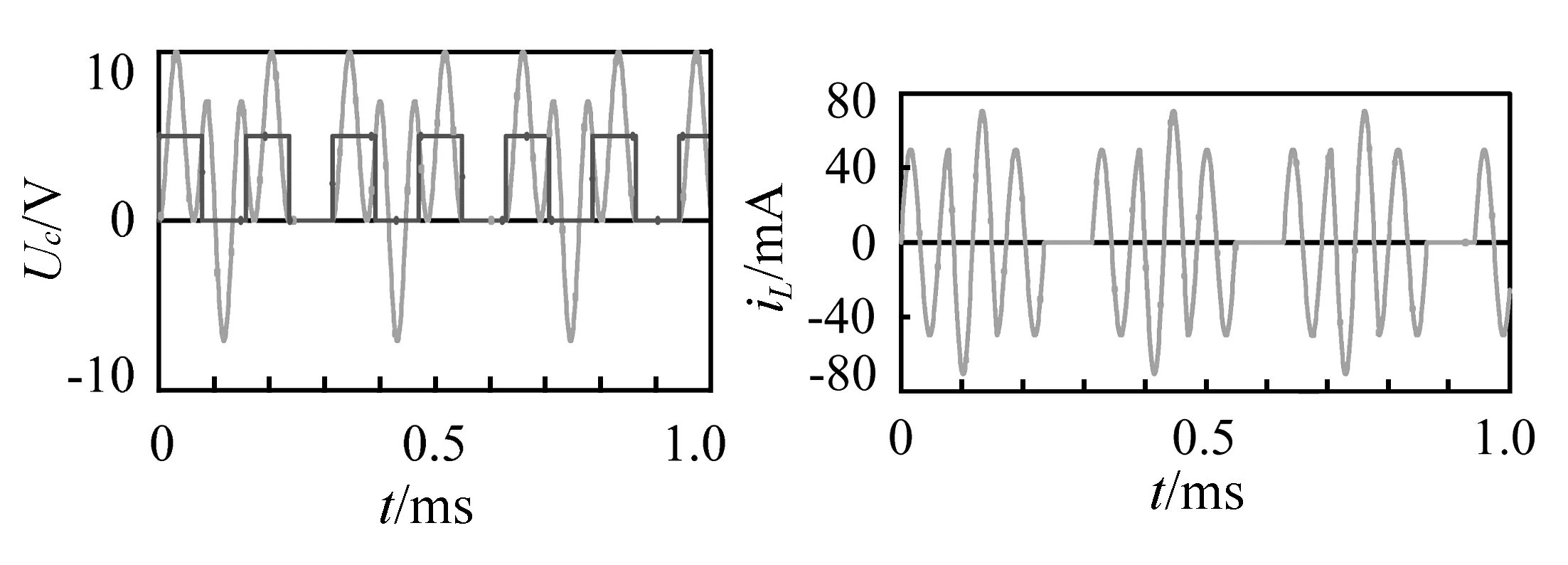
2.5 方波周期为振荡周期的n+1/2倍
2.6 方波周期为振荡周期的n+m倍(1/2
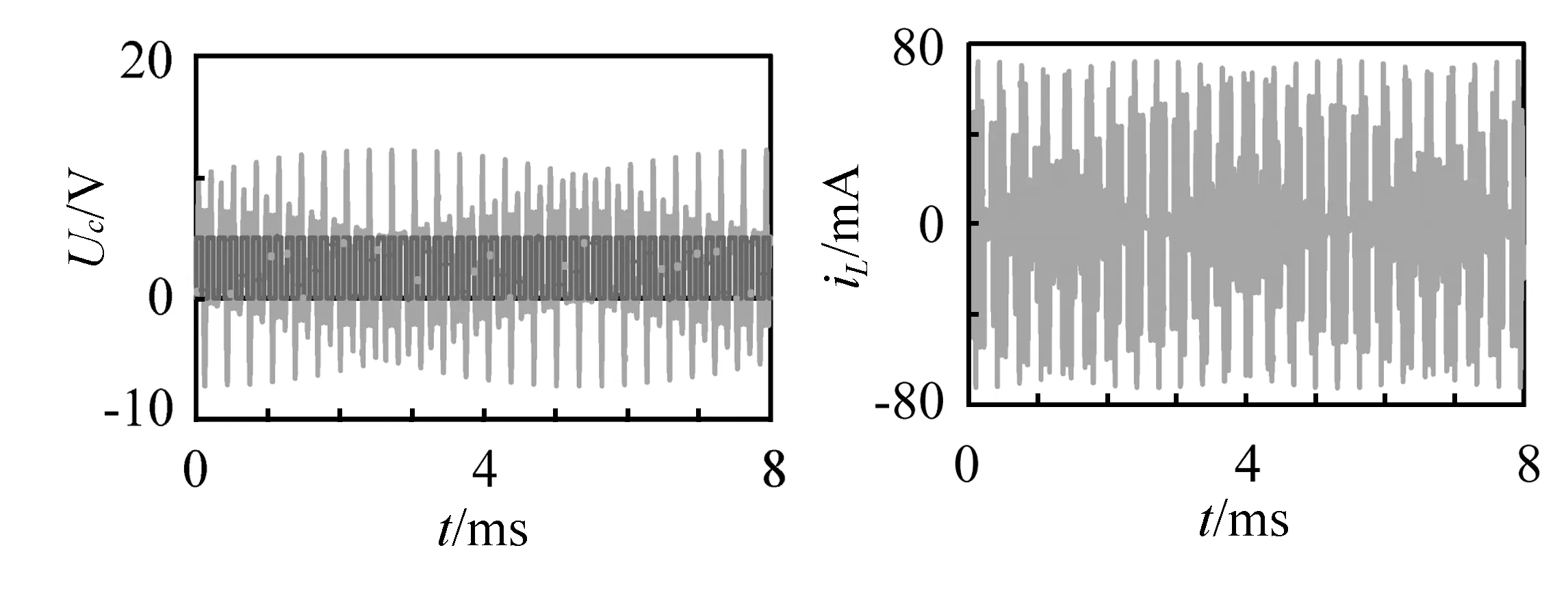
2.7 方波周期为振荡周期的n+3/4倍
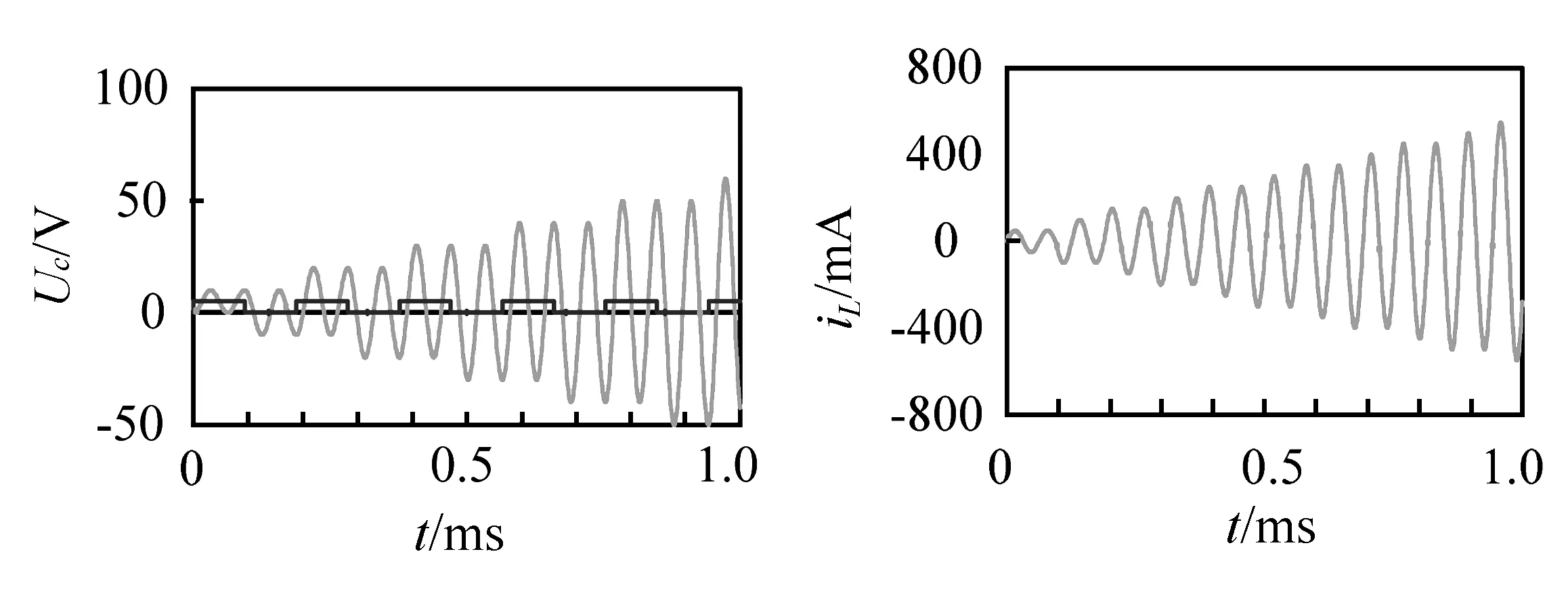
2.8 全响应
3 结论

