矩阵在优化模型中的应用

付小娟，吴洪坤

(1.广州民航职业技术学院 人文社科学院，广东 广州 510403；2.广州民航职业技术学院 机务工程学院，广东 广州 510403)

1 问题的提出

随着高校扩招规模的增大，许多学校都面临着教师的引进问题，而学校专业设置不同，需要招聘的教师背景不同，采用的面试手段也有所差异，而从一个学校的角度来看，如何根据自己的需求和应聘者的专业背景等相关资料来设计一场高效的面试，这是很多专家学者亟待解决的问题.根据相关统计发现：很多学校都把面试程序设计为初试，复试、试讲和面试4个阶段，现以广东某高校准备招聘6位新教师为例，根据每位应聘者的不同专业，分别预定出他们在每个阶段所需的面试时间，问题是如何安排这6位面试者的面试顺序才能既节省时间又提高面试效率.6位面试者时间分布表如表1所示：

表1 6位面试者的面试时间分布表 min

2 数学模型的建立

2.1 问题分析

问题就是如何根据这6位面试者的具体面试时间设计一个最节省时间的面试方案，这属于一个最优化模型[1]21-24，根据题中所述，关键是如何设定6位面试者的面试顺序，6个人的总面试顺序有720种，而面试顺序一旦确定，6位面试者在不同阶段的面试就完全遵循这一顺序约定，而不再更改.因此，这又是一个排序问题的最优化模型.要想节省时间，最要紧的是缩短等待时间，这里的等待时间包括求职者等待被面试的时间和面试考官等待面试求职者的时间，这两个等待时间必然都会使总面试时间增长，而不同的面试顺序将导致最终的总面试时间不同，其中，最短的总面试时间即对应最优的面试顺序.

2.2 模型假设与符号约定

假设所有面试者都能够参加完所有面试，中途不淘汰.所有面试考官都能按时参加完每一场面试.

假设每个面试者只有在进行完上一阶段面试后才能进入下一阶段面试.每个阶段一次只能面试一个人.

假设abcdef分别表示第1、2…6人，面试顺序约定为英文字母顺序.

符号约定：

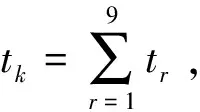
cBi,cBj表示矩阵B中从左到右第i条主对角线和第j条次对角线上的元素.

2.3 建模与求解

根据顺序性可知，面试过程的时间段数为r=m+n-1=6+4-1=9

假设面试顺序是a、b、c、d、e、f，则其对应的该面试问题的时间段图表为表2：

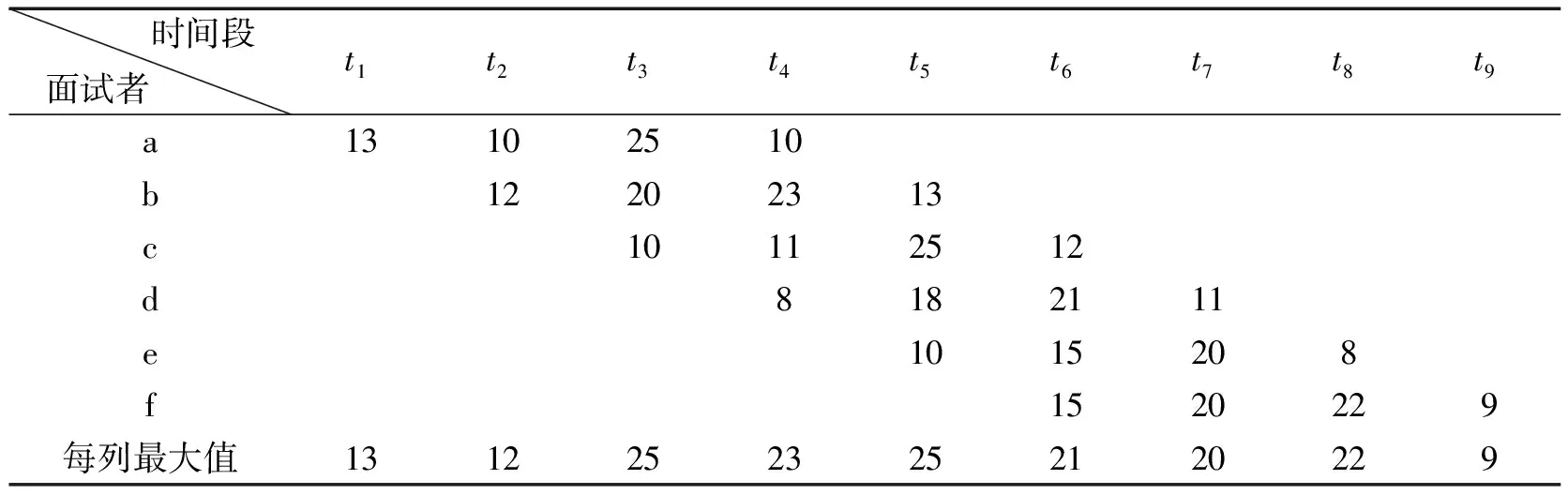
表2 面试顺序为abcdef时的9个面试时间段分布表 min

各时间段的意思：t3表示在此时间段内面试者a进行第三阶段即试讲，面试者b进行复试，而面试者c进行初试，以此类推.

由表2可知，在某个特定时间段的最大值所对应的时间内，此时间段内的所有面试都可以进行完，这里面已经涵盖了两种等待时间，所以，如果把各个时间段对应的最大值求和，那么其和就必然是该面试顺序下的总面试时间.如果，把表一看作一个矩阵[2]135-139，设其为A，则发现表2中时间段所对应的每一列数，正是矩阵A的次对角线以及与次对角线相平行的对角线上的元素，例如：t3时间段从上到下三个时间分别是25，20，10，这正是矩阵A中从左到右的第三条次对角线上的元素，为了能使tr对应的每列元素和矩阵的主对角线元素相对应，现转置矩阵A变为B，这时面试顺序按从右到左的顺序是abcdef，而其逆顺序是fedcba.

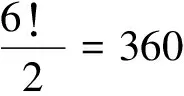
A：6位面试者的面试时间分布矩阵，从上到下，面试顺序是abcdef

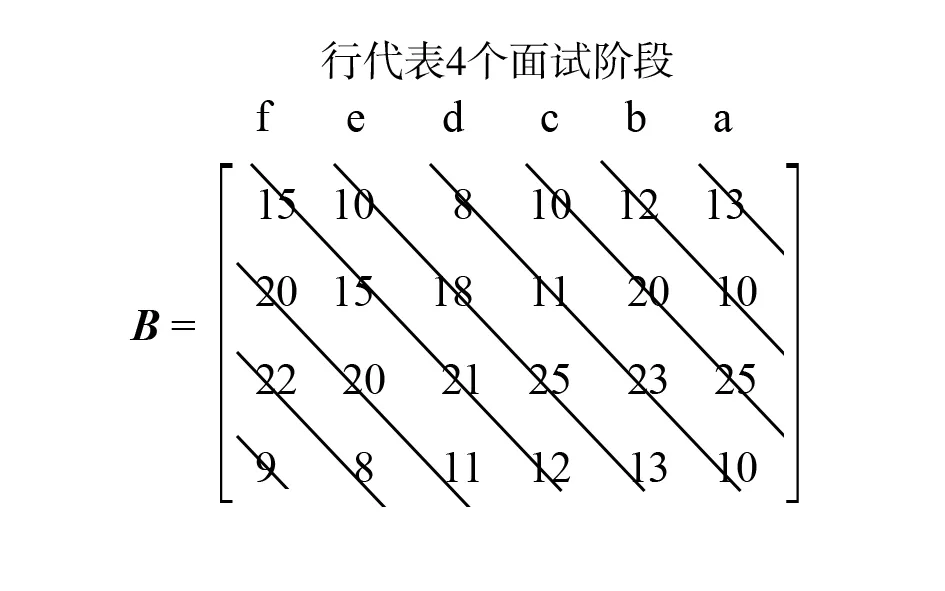
B：矩阵A的转置矩阵从右到左，面试顺序仍然是abcdef

计算出矩阵B的主对角线及与主对角线平行的各条线上元素的最大值，再求和就可以得到第一种面试顺序下的总时间：

即面试顺序为abcdef时面试所花费总时间为170分；而矩阵B的次对角线以及与次对角线相平行的各条对角线上最大元素的和为：

表示面试顺序为fedcabf时的面试时间为181分.更换矩阵B中第五列和第六列，面试顺序变为bacdef，计算出其主对角线及与主对角线平行的各条线上元素的最大值再求和，可以得到此种面试顺序的总时间，以及相反顺序的总面试时间；同理，更换矩阵B的第四列和第六列得到面试顺序为cbadef的总时间，以及面试顺序为fedabc时的总时间；如此反复交换算出所有面试顺序中所花费的总时间，其中，最小者就是总最短时间，相对应的就是最优的面试顺序，由此建立目标函数：t=mintk

最后利用C++语言编程计算，经比较得出最短总时间是165分，而其所对应的面试顺序为cdfbae,此即为最佳面试顺序.

3 结果与分析

当面试顺序为cdfbae时其对应面试时间段分布表为如下表3所示，发现其每列最大值之和刚好是165，表示总面试时间为165分，这165分已经包含了面试者等待被面试的时间和面试考官等待面试求职者的时间，在此时间内能够完成所有6个求职者4个阶段的面试，与C++程序所计算结果相吻合；而且从上表中可以看出每个面试时间段的等待时间，其中，面试者的总等待时间是64分，而面试考官的总等待时间为56分，两者非常接近，说明此结果比较接近实际情况.见表3.

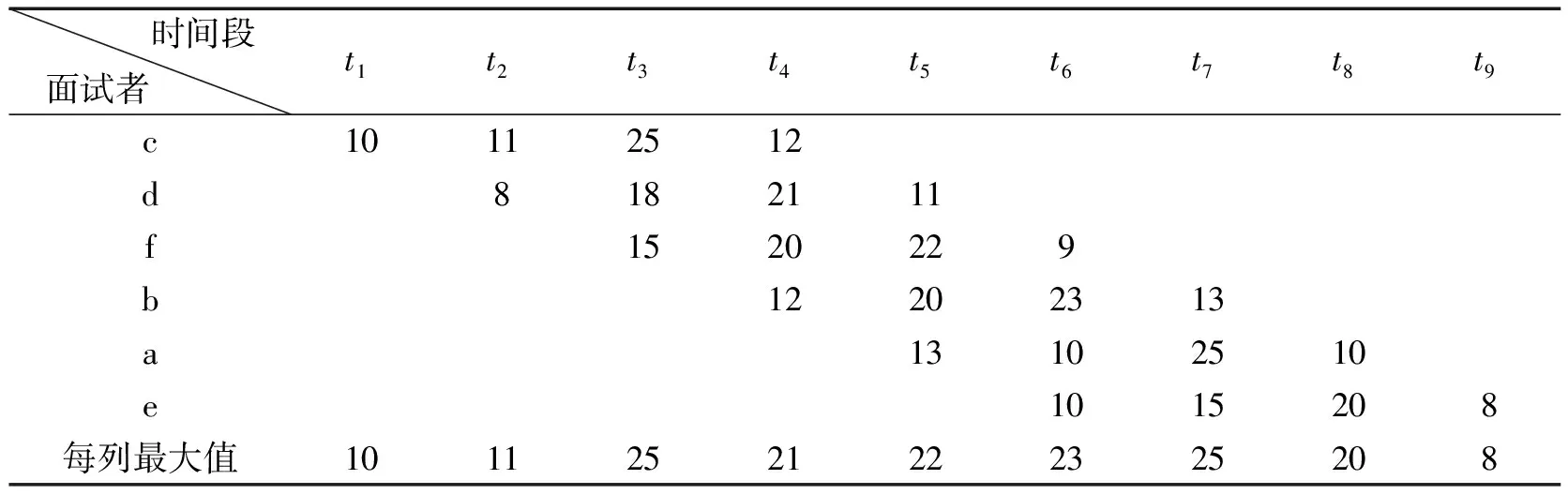
表3 面试顺序为cdfbae时的面试时间段分布表 min

设面试顺序为cdfbae时其对应的矩阵为E，可以发现矩阵E的每一条主对角元素刚好和表三中每一个时间段元素对应，主对角线元素中最大值分别为10，11，25，21，22，23，25，20，8，这些最大值之和为165，表明当面试顺序为cdfbae时花费总时间为165分，这和表3的结果吻合，也正是C++程序所计算的结果.

4 模型推广

此模型在处理时间方面假设的是每个阶段求职者的面试顺序是固定不变的，事实上，为了节省时间，再考虑到尽量不让面试考官等待求职者，而且实际招聘情况，通常应聘者通过初试后方可以进行以后3个阶段的面试，所以，此模型可以改进为第一阶段固定顺序，以后每一阶段的面试顺序灵活变动.另外，此模型通常适合于考场的安排、课程的编排[4] 240-242，[5]87-90、公司招聘人才的面试、高效择优录取以及产品的生产流程[6]60-62安排等方面,具有重要的应用价值.

参考文献：

[1] 但 琦，赵 静，付诗禄.数学建模课内容和教学方法的探讨[J].工科数学，2002，18(06).

[2] 王培麟.计算机应用数学:第二版[M].北京：机械工业出版社，2007.

[3] 宏道工作室.融会贯通visual C++6.0[M].北京：人民交通出版社，2000.

[4] 王 凤，林 杰.高校排课问题的图论模型及算法[J].计算机工程与应用学报，2009，45(27).

[5] 陶华亭，郭 玲.用图论方法解决排课冲突问题[J].郑州经济管理干部学院学报，2004，19(03).

[6] 赵家黎,梁角虎,胡赤兵.多工序制造过程错误工序的追溯[J].机床与液压，2009，37(10).