高压衰减器的时域校准方法

刘 阳，杨金涛

（北京无线电计量测试研究所，北京 100854）

引言

随着电磁兼容试验的广泛开展，应用于传导敏感度试验的脉冲信号发生器的使用频次大大增加，为保证电磁兼容试验和测试数据的准确、可靠，需定期对脉冲源进行校准。由于军用脉冲源具有上升时间短、重复频率高、脉冲源在50W 系统的最高输出电压达2kV 等特点，通常采用高压衰减器的形式对高压脉冲信号进行衰减后再通过示波器进行校准测量。因此，示波器上采集到的波形数据曲线是经过高压衰减器之后的波形，从而会引起测量结果的失真，无法得到准确的测试结果，需要根据衰减器的衰减值进行修正才能还原原始波形，因此高压衰减器的校准也是必不可少的。

通常情况下，高压衰减器的衰减系数是在频域测定的，频域校准法只能利用小信号，采用单频信号源进行，逐点测量不同频率下的衰减值并绘制成响应曲线。一方面小信号校准无法正确反映衰减器的高压特性。另一方面，频域校准只能得出被校设备的幅频特性，而并未反映相位信息，在衰减过程中存在较大时延时，无法正确还原原始波形，并且校准工作比较繁琐，需要逐点进行测量，并且在查阅时，对于没有校准到的频点，还需要进一步进行插值计算。

因此，本文介绍了一种高压衰减器的时域校准方法，采用该方法，只需要测量进入衰减器和从衰减器输出的两条时域曲线。通过数学处理的方法，可同时获取其幅频特性和相频特性，并且利用该方法，可在高压条件下对衰减器进行校准，直接反映高压衰减器的高压特性。

1 时域校准的理论

为了描述一个对象、过程或系统的特性，最简单、最能直接反映该系统性能的方法就是建立系统的数学模型。对于一个确定参数的系统，给系统施加一个输入产生一个响应的输出，这种输入输出有一一对应的关系。系统辨识就是通过测量系统的输入输出，加以必要的数据处理和数学计算，来获取该对象的数学模型，从而估算出系统的传递函数。

一个动态系统按其描述方法和分析、定义域的不同，可用不同的数学模型来表达，一般在经典控制理论中采用频域传递函数的方法来建模。其中，最常用的模型方式是参数模型，即用模型的参数来描述系统特性的模型，如微分方程和传递函数中的系数。对于一个线性连续系统可以分别用时域的微分方程或频域的传递函数来表示，连续时间、线性、定常系统，在单输入u(t)和单输出y(t)的情况下(SISO 系统)，可用高阶常系数线性微分方程来描述测量系统的动态特性：

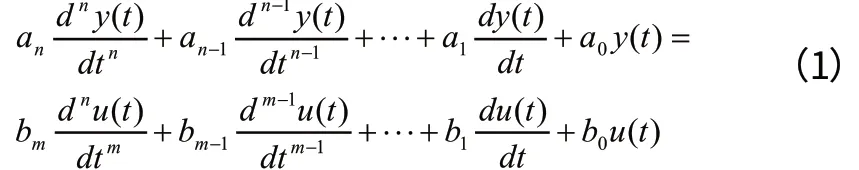
式中，u(t)为输入量，y(t)为输出量，a0,…an,b0…bn是系数，与测量系统的工作原理和结构有关。对上式进行Laplace 变换，得到其在零起始条件下的传递函数为：

由于通常在测试中获取到的测试数据是一系列离散的数据点，我们将上式改写为在离散状态下的数据关系，用高阶常系数线性微分方程描述离散输入输出系统的动态特性。

式中，u(k)为输入序列，y(k)为输出序列，e(k)为噪声。对上式进行Z 变换，得到传递函数为：

因此，在输入输出的时域波形数据已知的情况下，根据系统的结构特点，采用合适的数学模型，对系统进行建模，并根据输入输出数据进行数学解析，就可以得到系统的传递函数。

2 时域校准的方法

2.1 利用小信号对衰减器进行校准

采用小信号对衰减器进行校准，系统框图如图1 所示。

将信号发生器输出信号通过功分器分为两路，一路通过被校高压衰减器，经过衰减后进入示波器通道1，另一路直接进入示波器通道2，采用一组占空比为50%，频率为10kHz 的标准方波作为输入信号，如图2所示，经过高压衰减器的输出波形，如图3 所示。

对本系统建立辨识低阶系统精度较好的输出误差（OE）模型：

设置示波器参数，计算数据长度为1000，采样时间间隔为4*10-7s，设模型阶次n=5，设置系统延时参数，如果只关心衰减器的幅频特性，可忽略测量系统延时。经matlab 计算，得到系统传递函数参数A(q)和B(q)。从而可以得到以频率为变量的系统修正系数函数：

图1 小信号校准系统示意图

图2 输入波形

图3 经过衰减器的输出波形

将频率点代入该式，即可得到不同频率的衰减值，将其绘成曲线，如图4 所示。由于在计算时忽略了系统的延时，计算得出的数据信息是不包含相位信息的幅频特性，即幅度谱数据。如想获得系统的相频特性，可根据系统的实际结构，设置合理的时延参数带入模型计算。

2.2 利用高压信号对衰减器进行校准

前面提到过，利用低压信号进行校准无法正确反映高压衰减器的高压特性，为了进一步证明在高压条件下，该方法的可行性和准确性，我们需要进一步利用高压信号进行校准。按照图5 的连接方式搭建校准系统。采用一组正弦阻尼脉冲信号作为校准信号，同样将信号通过功分器分为两路，一路通过被校高压衰减器，经过衰减后进入示波器通道1，另一路直接进入示波器通道2。由于示波器在高阻状态下的输入电压值最大不能超过300V，在选择信号峰值时，将经过功分器后的电压峰值控制在200V 以内。

示波器通道2 测得的脉冲信号发生器的输出原始波形如图6 所示。

图4 小信号校准得到的修正系数曲线

图5 高压校准系统示意图

图6 输入波形

经高压衰减器衰减后的输出波形如图7 所示。同样利用系统辨识的方法，获得该系统的传递函数，即可得到在高压条件下，衰减器的幅频特性，如图8 所示。

3 结论

为了验证该校准方法准确性，我们利用频域校准方法逐个频率对该衰减器进行校准，将所得结果与以上时域校准结果进行对比,结果如图9 所示。

图7 衰减后的波形

图8 高压校准得到的修正系数曲线

图9 校准数据比对结果

由图9 可以看出，在小信号条件下对衰减器的时域校准结果与频域校准结果基本一致，然而通过时域校准省去了频域校准过程的繁琐步骤，可以通过一次时域测量经过数据处理后方便的获得高压衰减器的幅频信息和相频信息。

在200V 高压条件下，校准得到的衰减系数比以上两种结果略高，这是由于高压衰减器在高压条件下，内部的填充介质特性发生变化从而影响高压衰减器的衰减特性。由于示波器对输入电压值的限制，我们采用直接测量比对方法对时域校准结果的验证目前只做到200V，对于更高电压的信号，接下来需要进一步进行试验验证。

高压衰减器的时域校准可正确反映衰减器的衰减特性，高压衰减器的时域校准方法可广泛应用于各种高压衰减器的校准。

[1]刘卫东,刘尚合,魏明.高压脉冲激励的系统连续模型辨识与系统性能分析[J]. 高电压技术, 2010(10).

[2]石立华,陶宝祺等.脉冲磁场传感器的时域标定[J].计量学报,1997(2).

[3]樊高辉，魏明，刘卫超.基于系统辨识的电路脉冲响应建模[J].电讯技术, 2011(10).

[4]石立华,周壁华等.利用频域测量数据评价系统的时域响应特性[C].中国通信学会,中国电子学会,1999.

[5]胡广书.数字信号处理理论、算法与实践[M]. 北京：清华大学出版社. 2012.