大型武器平台天线辐射计算软件EMRC及其应用

王孟超，杨武，王健，李茁，陆卫兵

（1.东南大学信息科学与工程学院，南京 210018；2.东南大学计算机科学与工程学院，南京 210018；3.南京航空航天大学，电子信息工程学院，南京 210016）

引言

现代大型武器平台一般都安装有大量的通信、导航、雷达和电子战天线。然而，天线的工作环境对天线的实际性能有很大影响，可能造成远场方向图畸变、近场辐射危害等电磁兼容问题。因此当分析载体平台上天线的电磁特性时，必须考虑载体平台对它的影响。

在大型武器设备平台的电磁兼容问题分析中，由于问题规模非常庞大，全波方法的计算能力有限，高频近似法是解决这类问题比较有效的方法，其中弹跳射线法(SBR)[1]由于其适合计算目标几何结构之间的多次反射，并具有精度高，易于实现等优点，成为电大尺寸目标电磁计算的有效方法之一。SBR 算法中，首先构造了一个包围天线的虚拟口径面，然后考虑到SBR 算法的收敛性，将该虚拟口径面按照波长的十分之一进行划分，再根据射线追踪的思想追踪每一根射线管，最后利用几何光学和物理光学对光线追踪的结果求值计算。但是SBR 方法在射线管构建中存在着两大缺陷：一方面，SBR 解决电大目标构造射线数量庞大，影响计算效率；另一方面，SBR 不能精确处理复杂目标的微结构(缝隙、凸起等)，即射线管分裂问题[2]，这对计算结果造成很大误差。

本文结合理论和实际工程提出了适用于大型武器平台上的天线辐射问题数值计算的弹跳光束法(SBB)。SBB和SBR 最大的不同点就在于射线管构造，这一步是直接关系到算法精度和效率的关键步骤。不同于SBR 方法，SBB 方法中应用了一种称之为自适应射线管划分的思想[3,4]：用目标自身网格对口径面进行划分，即以光束的逆向投射裁剪代替了射线的主动发射循迹。这样就精确地描述出任意复杂目标的可见区域，避免出现数量庞大的射线管和射线管分裂问题。

基于SBB 算法，我们利用VC++开发出了具有人机交互界面的应用软件EMRC,并用它对舰船上的典型天线进行了仿真计算。

1 SBB 算法介绍

与SBR 方法一样，SBB 在射线管构建前首先要要构建一个虚拟口径面。此虚拟口径面要包围天线但是又不可以把目标包含进来。这里我们根据天线和模型的相对位置来构建一个立方体包围盒，如图1 所示。这个立方体的六个面即是接下来要被划分的初始口径面。

立方体的六个面是最初的虚拟口径面；O 点是天线所在位置，在立方体的中心；三角形ABC 是目标上的一个三角面片；三角形A’B’C’是目标三角形在初始口径面上的投影三角形。

SBB 方法中划分出来的射线管不能直接代入PO 公式来计算该射线管的散射贡献，原因是PO 积分中要保证入射的是平面波，然而此时得到的射线管只是根据模型划分出来的，并不能保证其可近似为平面波。所以在PO计算之前，要对射线管做细分处理，以保证其满足PO积分条件。

图1 构建的初始口径面及目标三角形在口径面上投影的示意图

下面分别介绍自适应射线管划分原理和远场PO 积分条件。

1.1 自适应射线管划分原理

自适应射线管的划分首先需要构建虚拟口径面，这里用包围天线的立方体的六个面作为初始的虚拟口径面，如图1 所示。

为了解决射线管分裂问题，我们变换了口径面划分和射线管追踪的顺序，先射线管追踪，仅在需要时再划分口径面。其计算流程大致如下:以构建的初始口径面作为初始射线管来追踪，在遇到目标几何结构时，根据三角形在口径面上的投影来动态划分射线管，使得一个或几个射线管完整地对应该三角形在孔径面上的投影区域。如此，口径面是根据目标的几何结构来划分，口径面上的分割线是目标在入射方向上可见三角形的边界投影线，每个射线管仅投影到一个三角形上，从而避免了射线管分裂问题。在得到一次入射的可见区域后，以这些区域作为下一步射线管追踪的口径面，依次对可见区域重复上述过程，得到每一区域的反射可见区域，如此迭代，直到射线管与目标不再相交，或超过最大反射次数。

1.2 PO 积分条件

在实际中，由于目标与天线的距离是有限的，所以入射到目标上的电磁波几乎都是球面波。本文中远场PO积分应用的是Gordon 公式[5]，近场的PO 积分应用的是改进的S.R.Legault 方法[1,6]，由公式的推导可知它们都是以平面波入射为假设前提的，所以在做积分时要保证入射场可以近似为平面波。故而需要确定在怎样的距离条件下，球面波入射波前可以作为平面波前的一个足够好的近似，这就是PO 的积分条件[7]。

为了得到PO 积分条件的具体表述，假设天线为点源，考察入射到目标不同宽度口径上相位波前偏离均匀的情况。根据图2 所示的几何关系，可以求得用距离R 和目标横向尺寸D 表示的最大路径差。

假设D≤2R，则有

因此，入射到目标中心与目标边沿处的电磁波相位差是kh，通常要求该相位偏移小于 π/8就认为近似平面波入射，于是得到PO 积分条件：

利用该PO 积分条件来细分划分出来的射线管，然后代入计算公式，算出该射线管的散射贡献。

2 EMRC 简介

基于上述算法，我们利用VC++开发出了具有人机交互界面的应用软件EMRC，如图3 所示。

用户在界面窗口中设置计算参数，导入目标模型和天线在自由空间中的方向图数据后，EMRC 即可以执行计算操作。EMRC 不仅可以计算出该天线在大型武器平台上的远场方向图畸变，还可以计算出天线附近武器平台上的近场分布。

计算出来的这些数据可以作为用户选择天线的种类、设置天线的最优位置的参考依据，从而将天线系统的电磁兼容问题最小化。

3 计算结果

接下来，通过舰船的两个算例计算结果和商业仿真软件FEKO 的对比，来说明EMRC 的正确性和高效性。该舰船尺寸为133.87m × 15.74m × 22.5m 。

3.1 算例一

考虑一个电偶极子天线，沿z 轴放置，工作频率为300M，现将该电偶极子天线放在舰船船首上，如图4所示。图5 给出的是远区|E|三维方向图计算结果对比；图6 和图7 分别是俯仰面和方位面的|E|方向图对比；图8 是近场分布|E|结果对比。

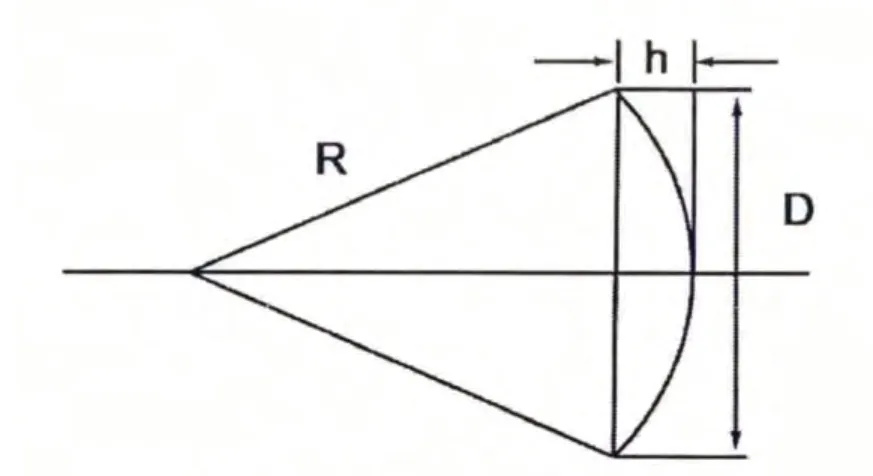
图2 球面波前在目标表面的相位偏移

图3 EMRC 的界面

图4 偶极子天线在舰船模型上的位置示意图

图5 电偶极子天线在舰首的远区|E|三维方向图

图6 俯仰面|E|方向图对比

图7 方位面|E|方向图对比

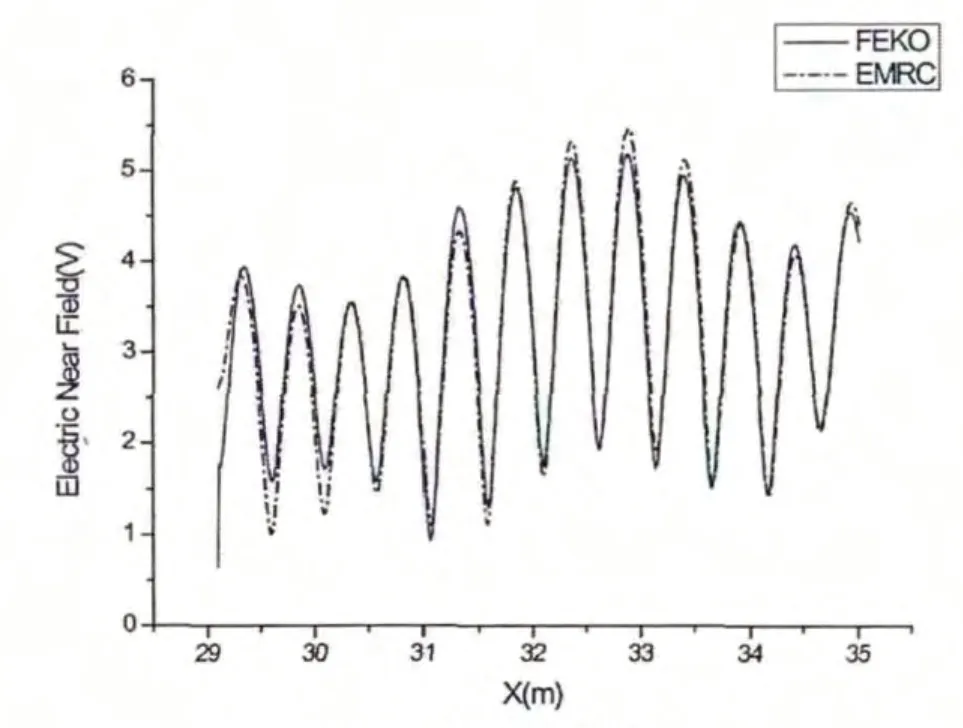
图8 近场分布|E|结果对比

以上算例在同一台服务器下计算。用FEKO-PO 方法仿真耗时1973s ，而利用EMRC 耗时377s。

3.2 算例二

考虑一个喇叭天线，喇叭口朝向x 的负方向，工作频率在1GHz，现将该天线放在舰船中部，如图9 所示。

此时该船的电尺寸大于400 个波长，在我们的实验条件下，FEKO 已经不能计算，所以下面只有EMRC 的计算结果。

图10 是喇叭天线在自由空间中方向图及其在舰船上的畸变方向图的对比；图11 为俯仰面|E|方向图；图12是近场分布|E|结果。

本算例EMRC 计算用时765s。

图9 喇叭天线在舰船模型上的位置示意图

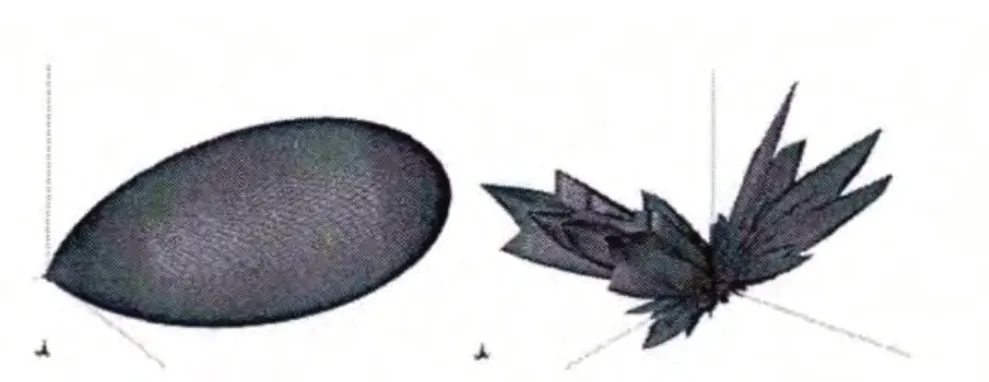
图10 喇叭天线在自由空间中方向图及其在舰船上的畸变方向图

图11 俯仰面|E|方向图

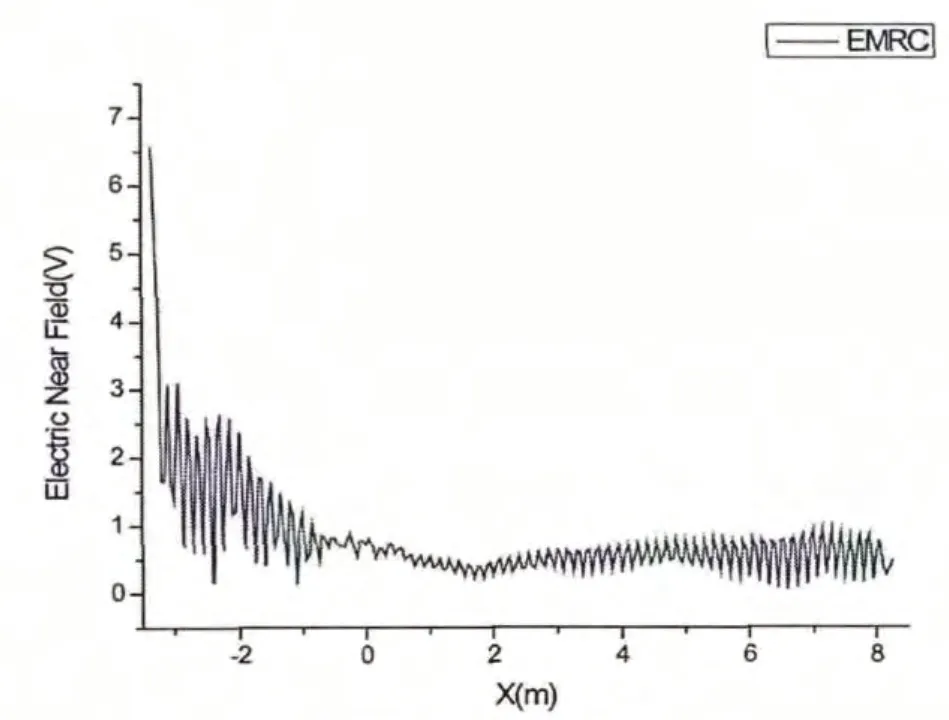
图12 近场分布|E|结果

在上面的两个算例中，EMRC 对舰船上的天线辐射进行仿真计算。通过在算例一中与FEKO 的计算结果对比，说明了EMRC 的正确性和高效性；通过算例二，说明了在同等计算条件下，EMRC 能解决问题的规模比FEKO 大，进一步说明了EMRC 的高效性。

4 结论

本文介绍了EMRC 的算法原理，并通过实际算例验证了它的正确性和高效性。未来，我们要在此基础上对软件做进一步完善：添加对数据的后处理功能，通过并行来加速计算等。

[1]刘朋朋. 复杂平台电磁兼容问题研究[D].南京：东南大学,2011

[2]陶煜波.基于图形硬件的快速电磁方法与系统[D].杭州：浙江大学，2009.

[3]TAO Y B, LIN H, BAO H J. Adaptive Aperture Partition in Shooting and Bouncing Ray Method[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(9): 3347-3357.

[4]冉喆.改进的Beam Tracing 高效电磁散射方法研究与实现[D].南京：东南大学，2012.

[5]William BG. Far-Field Approximations to the Kirchhoff-Helmholtz Representations of Scattered Field [J].IEEE Transactions on AP,1975,23(4) :590-592.

[6]Legault S R. Refi ning physical optics for near-f ield computations[J].Electronics Letters,2004,40(1).

[7]陶剑锋,盛孝鹏,孙青.复杂目标的近场散射特性分析[J].现代雷达，2006,10.