离心式机械振动台基本参数设计计算方法的探讨

邹振兴，邹蓓尼

（1. 苏州苏试试验仪器股份有限公司，苏州 215129； 2. 维苏威高级陶瓷（苏州）有限公司，苏州 215021）

引言

离心式机械振动台是一种能产生正弦振动的设备。由台体和电气控制等部分组成。凡额定质量在振动台允许下的元器件、仪器、仪表、家用电器及其它产品，均可以紧固在工作台面上作定频振动、扫频振动等试验。为试件提供实际使用可靠性能力的试验，也可作为振动工艺装备用。

目前国内的离心式机械振动台在结构上采用无强迫导向、四组轴离心力振动器、机械（或液压）同步调幅、空气弹簧支承、电子（计算机）控制自动扫频等先进技术；能分别进行垂直、水平两个方向的振动试验，完全能满足各类产品对振动性能的要求。

1 工作原理

激振源由装配于旋转轴上处于平衡位置的两个扇形重块及能任意改变两个扇形重块夹角α 的机构等组成。如图1 所示，当两个扇形重块处于平衡位置时，两个扇形重块旋转产生的离心力F1、F2大小相等、方向相反，激振合力为零。振动体系统（工作台面）处于平衡状态，不能激起振动。而通过调整两个扇形重块之间夹角α，这就改变了合力的大小，从而就使振动体系统（工作台面）激起振动，使振动体系统（工作台面）产生振幅（位移）、或加速度。而其每个扇形重块产生的离心力F 的大小为：

式中：

W：一个扇形重块的质量kg；R：扇形重块质心的距离m；ω：扇形重块旋转的角速度rad./see。

其离心力的合力F0可用余弦定理公式求得其大小为：

由（2）式可知，激振力的大小不仅取决于扇形重块的形体大小（即其质量和质心距离R 的大小）。还可通过调节两个扇形重块之间的夹角α 加以改变，当α 角为扇形重块扇面形夹角时，激振合力达到最大。

2 振动体系统的力学模型及其运动微分方程的解

该系统可抽象为一个单自由度的强迫振动，其系统的力学模型如图2 所示。按牛顿定律，其运动微分方程为：

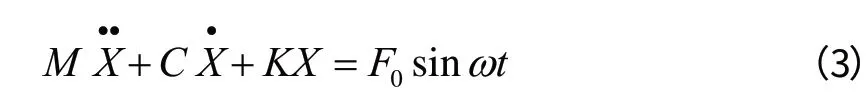
实际上摩擦阻力是相当小的，为简化计算，可先将次要因素阻力略去，经实际测量证明由此推导得出的公式，其振幅（位移）计算结果是足够准确的，其误差仅为0.1mm。

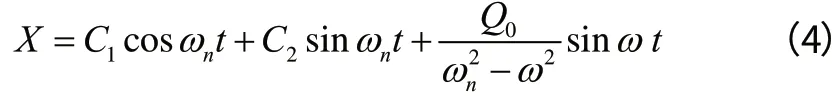
3 强迫振动的振幅、最大加速度和激振力的计算

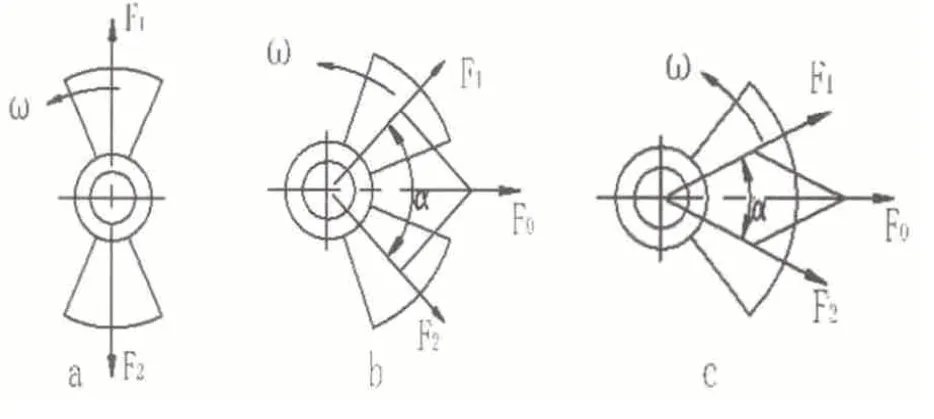
图1 a.两个扇形重块处于平衡位置 b.两个扇形重块处于任意夹角α 位置 c.两个扇形重块处于任意夹角（极限）位置

图2 系统力学模型图

3.1 强迫振动的振幅

由于摩擦阻力的实际存在，使（4）式中前两项自由振动逐渐衰减为零，只剩下最后一项，因而出现了强迫振动的平稳阶段，这就是我们设计强迫振动的依据。

即：

振幅 A 即为最大位移时，其值可用下式表达：

从（6）式可见,振幅的大小取决于振动体系统的强迫频率ω 与振动体系统的固有频率nω 之比。两者接近时，振幅就增大，从而就发生共振。

本机为超共振运行，也就是说，振动体系统工作频率（即强迫频率）ω 总是大于振动体系统的固有频率nω 。

当：ω >>ωn并将（1）代入（6）式，就得到振幅A 的下面的表达式

式中：Me =WR 为扇形重块的质量与扇形重块的质心距离之剩积，称为静力矩kg .mm；Ws - 振动体系统的质量kg。

亦即当振动体系统的强迫频率ω 远远高于振动体系统的固有频率nω 时，其振幅值的大小为总静力矩Me 与活动部分（振动体系统）总质量Ws 之比，即导出了振幅与频率无关的这一似乎难以令人置信的结论。这是一个非常简明而有用的结论。按此式可进行振动台振幅的设计计算。

（7）式的应用条件为ω >>nω 。为了保证在作恒振幅扫频试验时，振幅能稳定，其波动不会超过10%，则按（6）中的系数计算可以得出：振动台工作频率的下限至少要高出振动体系统的固有频率的3.5 倍以上，高出越多越好，在振动台的振动体系统中，一般取为4 ～ 5 倍。

3.2 强迫振动最大加速度 a

由（5）式得强迫振动的位移为：

将（8）式对时间t 求导二次，则就得到加速度 a ：

式中：f 为强迫振动频率，其单位为Hz（赫兹），A为振幅，单位为mm。

从（10）式我们可以看出：振动频率、振幅和其对应的加速度三者之间的关系，只要能知道其二，就可以求出第三项。

式中：Ws ：振动体系统的总质量，kg； a0max：振动体系统的加速度，m/see2。

（11）式亦即为最大激振力等于振动体系统的总质量Ws 与对应频率、位移时最大振动加速度 a0max之乘积。

按上述的有关公式，我们就可以设计计算出满足不同能力、不同使用要求的离心式机械振动台；并能对已有的机械振动台的能力进行校验和预置振动试验参数。

4 振动体系统的固有频率及空气弹簧设计计算

4.1 振动体系统的固有频率 fn

式中： K：弹簧刚度，kg/cm；g：重力加速度，981cm/see2；sW ：振动体系统的质量，kg。

从式（12）可以得出：振动台的振动体系统的总质量MS及其支承弹簧 k 值决定了该振动体系统的最重要参数-固有频率，所以弹簧是振动台的基本要素和重要的零部件之一 。

在诸多种弹簧中，空气弹簧由于 k 值小，因而振动体系统固有频率fn可设计得很低。这样可使振动台工作频率下限较低，此外，当振动体系统的质量改变而使振动体系统中的工作台面偏离设计的平衡位置时，可向气室充气或放气，很方便的将振动体系统中的工作台面升降，将其调节到设计的平衡位置，其它诸如没有金属接触、摩擦而带来的各种缺陷等等。

4.2 空气弹簧结构尺寸及工作原理

图3 为一空气弹簧结构及尺寸图，主要由三大件，即活塞、皮囊和气室组成。活塞与振动台的振动体系统的工作台面相固接。

当振动台的振动体系统的工作台面垂直向下运动时，与其固接的活塞就压缩密闭于气室中的空气，同时整个气簧结构对活塞产生一个向上的反力，这就是空气弹簧。

4.3 空气弹簧常数K 值计算公式的推导

4.3.1 活塞作用力F 的表达式

如图4 所示，当活塞由静平衡位置下移一距离 x （实际上就是振动体系统的位移）时，整个气簧对活塞将产生一个向上的反力。设此时气室内的气压为 P ，此反力由二部分组成，一个是由于气压 P 作用于直径为d0的面积而产生的力F塞，直接向上反抗活塞；第二个力为皮囊在气压 P 作用下对活塞产生的向上提升力 F皮。其值为：

从图4 中作I-I 截面，将皮囊切开，得到内环截面上的内力 F内。而 F皮与 F内是等值而反向的，故有其值为：

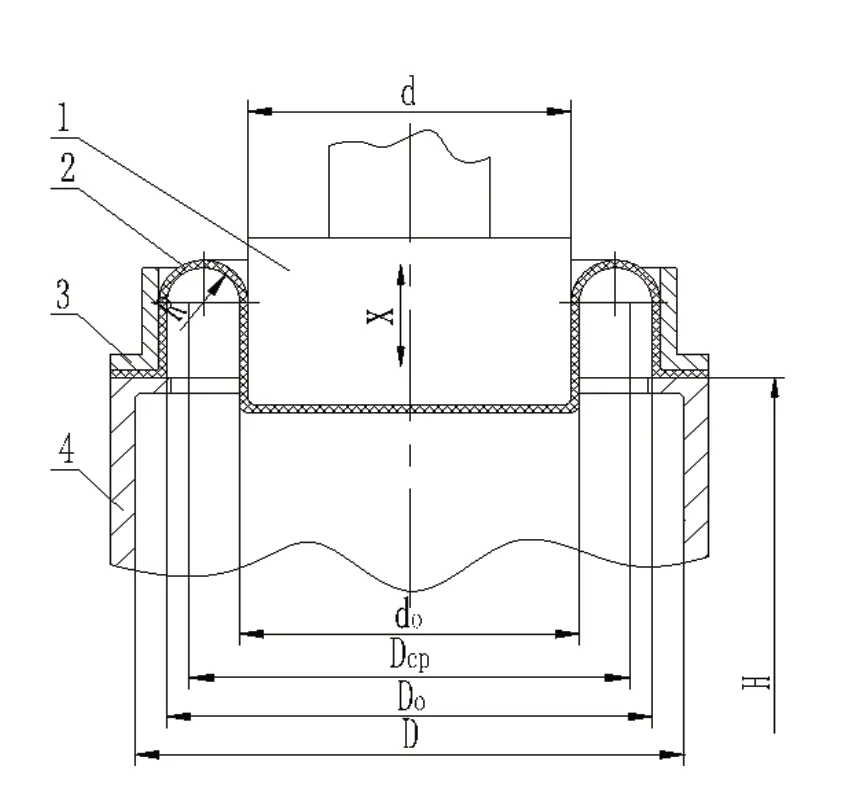
图3 1.活塞 2.气囊 3.压圈 4.气室po：初始气压 Do：初始空气体积

按作用力、反作用力定律可知：活塞向下运动的阻力为：

式中：Dcp ：计算承受气压力面积的直径，其计算式为：

4.3.2 气室空气体积υ 的表达式

如图5 所示，当活塞向下移动一距离 x 时，气室中的气压由P0（气室空气初始压力） 提高到P，而其容积也同时被压缩，由0υ （气室空气初始体积）降为υ。若将环圈 R 想象成整圈，这就构成了一个“动滑轮”机构。当活塞下移 x 时，“动滑轮”的轮心将同时下移故环圈下移被压缩了的空气容积为：

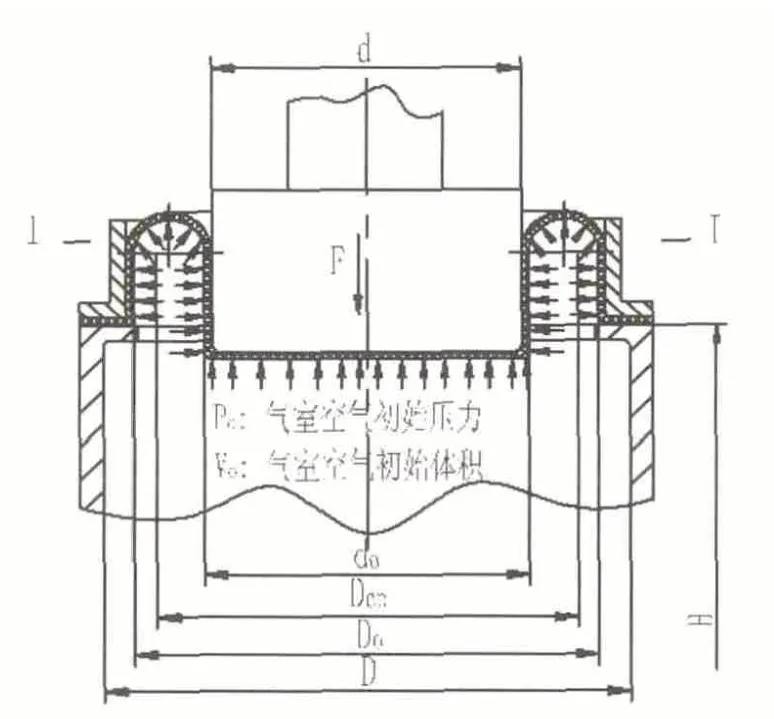
图4 气室内气体作用力图

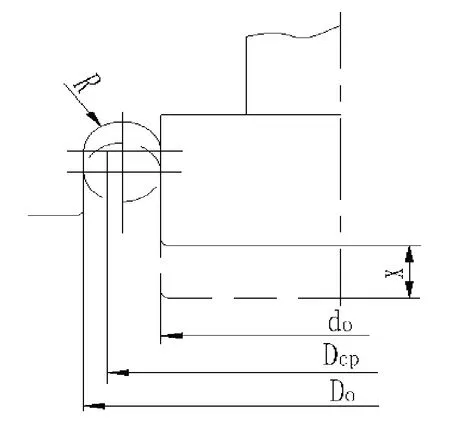
图5 气囊（活塞）运动模型图

这样被压缩后的体积为：

4.3.3 空气弹簧常数 K 值的计算公式

分析弹簧常数 K 值表达式中有关各项参数可知：在其它参数不变时，适当减少活塞直径，可有效降低弹簧常数 K 值，即弹簧刚度。

5 应用举例

已知某离心式机械振动台的主要性能技术参数为：额定频率范围：5～60 Hz，空载额定位移（峰-峰值）10mm，额定加速度：100m/s2，额定负载：250kg，等等。要求计算出：扇形重块的质量W1及质心距R；振动体系统的固有（下限）频率。

5.1 计算总静力矩Me

振动台的振动体系统的质量为Ws = 255kg 左右，则其静力矩为：

5.2 确定扇形重块的质量W1 及质心距R

扇形重块产生的力矩Ms 必须大于振动体系统的静力矩Me。而该形号的离心式机械振动台，是由四组相同的扇形重块组成，所以一组扇形重块所需要的力矩为：

5.2.1 扇形重块质量的计算

扇形重块有关尺寸如图6 所示。其体积V1、质量W1为：

式中：7.8 为钢材的比重，单位为：g/cm3，W1的单位为kg。

则一组扇形重块合成质量W合1为：

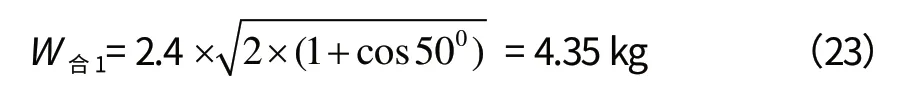
5.2.2 计算扇形重块质心距离R

5.2.3 计算扇形重块产生的力矩Ms

从目前计算的结果，扇形重块产生的力矩Ms 大于振动体系统的静力矩Me，可用。而实际生产的振动台振动体系统的实际质量为257.5kg，其实际的静力矩为：

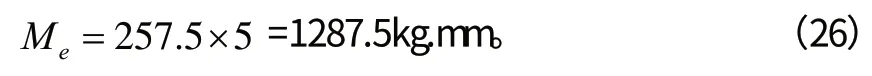
由此可以得出：上面设计计算确定的扇形重块的结构尺寸所能达到的力矩符合使用要求。

5.3 计算振动系统的固有（下限）频率f

振动体系统的工作台面是水平支承在四组空气弹簧上的，且四组空气弹簧是并联接的，即每一个空气弹簧承受的载荷是相同的。所以振动体系统（工作台面）要作静平衡检查与调整。

5.3.1 计算空气弹簧常数k

按该型号的振动体系统相关参数和图3 所示的空气弹簧结构尺寸代号，我们设计了空气弹簧结构尺寸为：其单位均为mm。

计算承受气压力面积的直径Dcp：

图6 扇形重块结构尺寸图

计算承受气压力的面积Acp：

计算空气弹簧气室初始体积0υ ：

计算空气弹簧常数k：

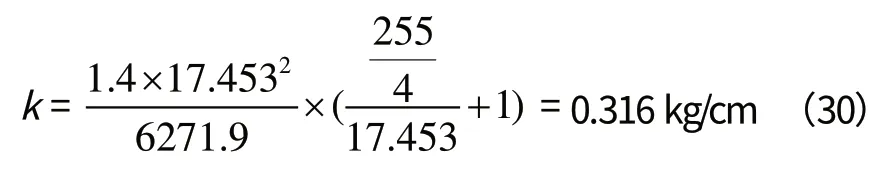
5.3.2 计算振动系统的固有（下限）频率f

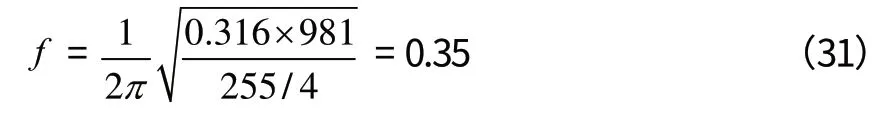
我们用扫频的方法对该型号机械振动台进行了测试，其结果是：垂直方向振动时，其固有频率为：fn= 0.5-0.6 Hz；水平方向振动时，其固有频率为：fn= 0.9-1.2 Hz。可以满足使用要求的。

6 结论

总之，要计设一台性能、功能良好的离心式机械振动台，除了理解、熟练运用和掌握上述推导的计算公式外；还必须要事先能精准预计振动台振动体系统的总质量WS，这一点至关重要。

[1]维屏 主编. 机械振动学[M].北京：冶金工业出版社,1983.

[2]清华大学工程力学系固体力学教研组振动组 编.机械振动[M].北京：机械工业出版社,1980.

[3]谷口修 主编.振动工程大全[日][M].尹传家译.北京：机械工业出版社,1986.

[4]樊映川 编箸.高等数学[M].北京：人民教育出版社,1959.

[5]上海高等工业学校物理学编写组 编.普通物理学[M].上海：上海科学技术出版社,1960.

[6]浙江大学液压教研组 编.液压与气压传动[M].北京：机械工业出版社,1980.