射流孔入射雷诺数对循环射流混合槽内流场特性影响研究

王 伟, 吴剑华, 禹言芳, 刘笑任, 孟辉波

(1.沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142;2.辽宁省高效化工混合技术重点实验室， 辽宁 沈阳 110142)

化学工业与我们的生产和生活密切相关，是我国国民经济的支柱产业，为我国社会经济发展和国防建设提供了重要的基础材料和能源[1].化工生产中的混合单元操作设备是化学工业过程中的核心设备，也是能源消耗的主要设备[2-3].搅拌设备适用于物料的混合、传热、传质以及制备乳液、悬浮液等，被广泛应用于工业生产中.机械搅拌是工业上实现多相流体混合的传统装置，其原理是通过叶轮的旋转把机械能传给流体物料，在多尺度流体间形成强制剪切流，混合过程即为在该强制对流作用下的强制扩散过程.传统的混合装置有很多有待改进的地方，尤其是大储罐和地下储槽，其操作及维护费用很高[4]，而射流混合设备在节能降耗、安装难易程度及密封性能等方面显现出很多优势，从而使其在工业上的应用越来越广泛[5].

新型循环射流混合槽作为一种新型的化工过程强化设备，其主要技术特色是利用外循环射流混合取代传统机械搅拌，致使槽内流体在很短的时间内达到高效混合，大幅降低能耗和维修费用，有效地解决密封等问题[6-12].到目前为止，国内外对该混合槽内流场特性的研究较少，数值模拟停留在稳态流场分析[9,12]，实验研究仅对循环射流混合槽内压力波动进行分析[8,10-11]，未见对混合槽内多孔耦合水平射流流动特性的研究.因此，针对其结构特点，本文采用计算流体力学方法研究不同射流孔入射雷诺数对新型循环射流混合槽内多孔耦合水平射流流场特性的影响，为今后开发具有高性能的混合设备提供理论参考依据.

1 循环射流混合槽几何结构

循环射流混合槽物理模型为文献[8]的简化特征单元，包括主体部分与循环管路部分.其中循环射流混合槽槽体直径D=0.4 m，槽体高H=0.24 m，混合槽内对称布置4块挡板构成主体混合部分；提升管(上开有3个小孔)、中心环管以及降液管(四面开有槽型排液孔)共同构成混合装置的液体循环部分，各结构尺寸及参数如图1所示，其它混合槽尺寸参见文献[8-9].

图1 数值模拟模型及动量源加载区域示意图Fig.1 Schematic diagram of circulating jet tank and momentum source

2 数值模拟策略

2.1 湍流模型选择

Zughbi等[13]在研究单喷嘴循环射流混合槽时指出，混合槽内部流动状况取决于喷嘴处流体入射雷诺数(Rej=DjUjρ/μ).若雷诺数小于300，则射流为层流；而当雷诺数大于1 000时，可以认为混合槽内部流动状态为完全发展了的湍流.本文最小流速时射流孔处雷诺数为3 664，因此，可以认为各参数下混合槽内部流场处于完全湍流状态.前人在单喷嘴射流混合器的研究中，使用标准k-ε模型成功地预测了混合器的流动特性及混合时间[14-16].他们的研究同样证明标准k-ε模型与雷诺应力模型相比，误差仅为1 %，而计算时间则远小于雷诺应力模型.结合前人的研究及本课题的研究对象，本文的湍流模型选用以下标准k-ε模型.

2.2 数学方程

标准k-ε模型适合完全湍流的流动过程模拟，流场中的流体运动满足质量守恒方程：

(1)

同时，也满足动量守恒的N-S方程：

(2)

分子黏性的影响可以忽略[17]，湍动能方程：

Gκ+Gb-ρε-YM

(3)

耗散率方程：

(4)

式中：ρ为流体密度，u为流速，Gk表示由平均速度梯度引起产生的湍动能，Gb表示由浮力影响引起产生的湍动能；YM表示可压缩湍流脉动膨胀对总的耗散率的影响.湍动能黏性系数μ=ρCμk2/ε.C1ε=1.44，C2ε=1.92，C3ε=0.09，湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0，σε=1.3.

2.3 动量源方法

为了实现混合槽内流体循环流动，使用UDF自定义函数，在进料管处添加一段动量源区域.动量源加载区域如图1所示.加载动量源区域管路长度为0.076 m，管路直径0.032 m，加载动量源后，流体在该区域流动方向为沿x正方向.

2.4 物理模型及边界条件

主体与循环管路重合截面均设置为interface，以允许流体流过；加载动量源的部分单独设置边界条件；混合槽壁面定义为静止壁面边界条件，采用无滑移边界条件和标准壁面函数法，不考虑壁面传热；混合槽液面定义为自由液面，液面处无剪切力存在，平均速度为零，轴向和切向速度梯度也为零.

2.5 初始条件设定

首先在稳态条件下求解宏观流场，此时只需求解动量方程和湍动能变量输运方程，因此，初始条件设定为：ui=k=ε=0.

3 分析与讨论

3.1 网格无关性验证

网格疏密程度对数值模拟结果的精度以及计算时间都有一定的影响.但对于一个给定的具体问题，网格的密度达到一定程度时，进一步的加密网格对计算精度影响并不明显，反而却延长计算时间.模拟计算时，首先对节点数分别为425 510，318 824和142 490的三种不同密度网格进行模拟.三种尺寸下网格的最大扭曲率均小于0.85，符合网格质量要求.

因此，选取三种不同网格策略对射流孔间距C2/dj为13.3、入射角度γ为30°的三层射流孔结构的循环射流混合槽内流场特性进行数值模拟，并分析中间射流孔射流特性.其中心线速度衰减规律如图2所示.

图2 三种网格尺寸下中间射流孔纵向速度分布Fig.2 Effect of grid sizes on jet axial velocity

从图2中可以看出：中等网格和精细网格曲线非常接近，而粗糙网格则有较大差异.结果表明：网格尺寸为6 mm(粗糙网格)时的纵向速度与网格尺寸为4 mm(精细网格)和5 mm(中等网格)相比，最大差别达48.70 %和41.30 %.而网格尺寸为5 mm时的纵向速度与网格尺寸为4 mm时在93 %范围内最大误差均小于5 %.因此，综合考虑计算精度及计算时间，选取网格尺寸为5 mm的网格划分策略，整个计算域共划分1 722 688个网格单元，318 824个节点.

3.2 纵向速度分布规律

使用动量源方法对不同射流孔雷诺数下新型循环射流混合槽流场特性进行数值研究，射流孔处入射雷诺数Rej分别为3 459～31 622.图3为不同入射雷诺数下射流轴截面纵向速度分布曲线.

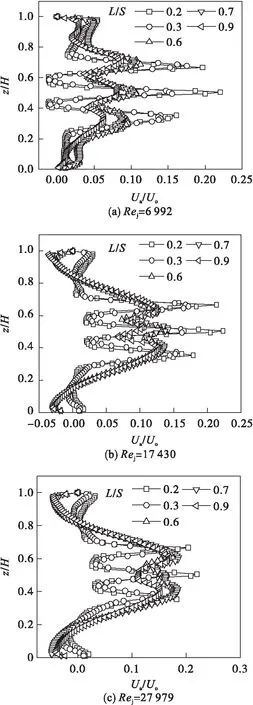
图3 不同入射雷诺数下射流轴截面纵向速度分布规律Fig.3 Distribution of jet axis velocity with different Rej

从图3中可以看出：在各流量下的射流初始段，纵向速度呈现出三个明显的正波峰，在这三股射流的中间形成了两个负压区域形成的低速区域.在射流孔雷诺数小于17 430时，该低速区域纵向速度为负值，该部分区域的无量纲纵向速度随射流孔雷诺数增大而增加.从图3中还可以看出：小流量下，射流轴截面纵向速度分布始终呈现出三股射流独自发展的特性；在射流孔雷诺数大于17 430的图中可以看到，靠近射流末端的壁面区域附近，三个速度波峰逐渐发展为两个波峰，这说明随着初始流量的增大，三股射流的卷吸与掺混也逐渐加强，两两互相影响，三股射流最终发展为两股射流.

喷射纵向初始区域内，z/H大于0.9及小于0.1的上下底面区域纵向无量纲速度几乎为零.射流孔处入射雷诺数Rej小于17 430时，壁面区域变化较小，说明小流量下射流能量主要集中在混合槽内中间区域，对混合槽内上下壁面区域影响较小.射流孔处入射雷诺数Rej大于17 430时，混合槽内上下底面纵向速度变化随流量增加而加剧，较大射流孔入射雷诺数下，射流随着射流路径的增加，影响范围也从射流孔附近逐渐扩散至混合槽所有区域.

从上面分析可以看出：射流孔入射雷诺数17 430以下，射流影响范围主要集中在z/H=0.2～0.8，而射流孔入射雷诺数大于17 430时，多孔射流影响范围扩大到混合槽所有区域.z/H=0.2及z/H=0.8附近，纵向无量纲速度很小，为纵向速度由正至负的过渡区.

3.3 中心线速度衰减规律

图4为不同射流孔入射雷诺数下中间射流孔无量纲中心线速度衰减曲线.从图4中可以看出：不同入射雷诺数下，射流无量纲中心线速度衰减趋势大体一致，均在射流孔附近迅速衰减，并在L/C2=1.5左右开始稳定.流量较小时，无量纲中心线速度衰减趋势基本呈线性递减.随着雷诺数增大，衰减趋势趋于平缓，Rej大于27 979时，无量纲中心线速度在L/C2=1.5附近不但没有衰减，反而增加，直至L/C2=2.5，之后才逐渐衰减至无穷小.这说明在较大射流孔入射雷诺数时，各射流孔间相互作用比较剧烈，在L/C2=1.5～2.5时，多股射流相互作用不仅能减缓速度衰减趋势，甚至能形成如图所示的一段速度递增区域.

图4 不同射流孔入射雷诺数下无量纲中心 线速度衰减规律Fig.4 Distribution of jet axis velocity decay with different Rej

根据射流轴截面距离射流孔的距离，可以将不同射流孔入射雷诺数下无量纲中心线速度衰减曲线近似看为三段线性递减的函数.L/C2小于0.4附近为射流初始段快速衰减区，速度与距离关系见式(5).大于0.5≤L/C2≤1.5的区域为过渡段较快速衰减区，该区域函数关系见式(6).1.5≤L/C2≤3.2的主体段区域内，雷诺数小于或等于24 506时，中心线速度衰减缓慢，速度与距离关系见式(7).L/C2=0.4～0.5区域无量纲中心线速度线性递增，此区域为三股射流的汇聚区，在这段区域之前，无量纲中心线速度与距离关系式斜率绝对值较大，射流中心线速度急剧衰减；在此区域之后的两段区域，斜率绝对值减小，中心线速度衰减趋势减弱.

Ua/U0=-6.67L/C2

(5)

Ua/U0=-0.88L/C2

(6)

Ua/U0=-0.66L/C2

(7)

从图4还可以看出：无量纲中心线速度在L/C2大于1.5的区域内基本随着射流孔入射雷诺数的增大而增大.这说明射流孔入射雷诺数的增大不仅有利于各股射流之间的相互作用，而且也有利于中心线速度与初始速度的比值保持在一个较高的范围，以达到节约能耗的目的.值得一提的是Rej=10 470的无量纲中心线速度大于Rej=13 977，这说明并不是入射雷诺数的增大一定会提高无量纲中心线速度的绝对值.在特定的操作参数一样的情况下，射流孔入射雷诺数相近的两组无量纲中心线速度有可能雷诺数低的无量纲速度反而高，这说明Rej=10 470时，三射流孔射流的相互作用比Rej=13 977时更好.

3.4 轴截面流速分布相似性

不同射流孔入射雷诺数下，新型循环射流混合槽射流末端靠近壁面处射流轴截面纵向速度自相似性分布如图5所示.从图5中可以看出：较大的射流孔入射雷诺数与较小射流孔入射雷诺数相比展现出更好的自相似规律.随着雷诺数的增大，三股射流汇聚成两股射流.Rej小于13 977时，射流末端轴截面纵向无量纲速度存在三个明显的峰值，其半值宽b1/2基于其中最大峰值的最大速度.

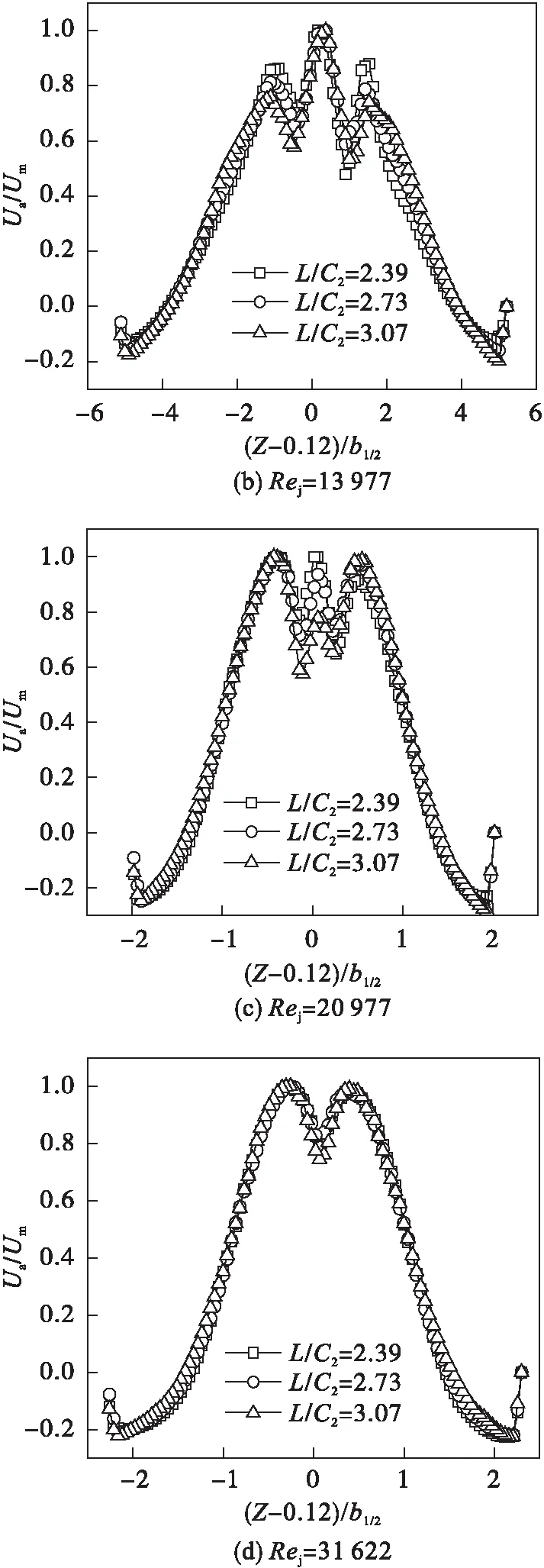
图5 不同射流孔入射雷诺数下射流轴截 面流速分布自相似性Fig.5 Velocity slef-similarity of jet axis cross-section with different Rej

随着雷诺数增大，纵向无量纲速度逐渐由三波峰发展为两波峰，其半值宽也随之增大.射流孔入射雷诺数小于13 977时，三个纵向无量纲纵向速度波峰的位置基本与射流孔位置重合，并且靠近壁面的两个波峰随着流量增大逐渐向中间射流孔发展.而当射流孔入射雷诺数大于13 977时，三股射流逐渐发展为两股射流，中间射流孔的速度波峰也随着两边两股射流的相互作用而逐渐减小.并且这种现象在Rej=31 622时完全消失，三股射流则发展为两股射流.两股射流速度波峰则位于三射流孔两两相间的中间位置，这也进一步说明在较大初始流量下，新型循环射流混合槽受限空间内的三股射流能汇聚成两股射流.

4 结 论

本文采用标准k-ε湍流模型对不同射流孔入射雷诺数下循环射流混合槽内多孔耦合水平射流流动特性进行了数值模拟，并分别分析了射流轴截面纵向速度分布、中心线速度衰减及其自相似性在不同射流孔入射雷诺下的变化规律，得到以下结论：

(1)Rej≤13 977时，射流末端轴截面纵向无量纲速度存在三个明显的峰值，三个纵向无量纲纵向速度波峰的位置基本与射流孔位置重合，并且靠近壁面的两个波峰随着流量增大逐渐向中间射流孔发展.而当Rej>13 977时，三股射流逐渐发展为两股射流，中间射流孔的速度波峰也随着两边两股射流的相互作用而逐渐减小.在Rej=31 622时，三股射流则发展为两股射流，两股射流速度波峰则位于三射流孔两两相间的中间位置；

(2) 射流孔入射雷诺数的增大，减弱了射流中心线速度与初始速度比值的衰减趋势，同时强化了射流轴截面纵向速度自相似分布程度，当Rej=31 622时，三个轴截面处纵向速度分布几乎重合.

参考文献：

[1] 孙宏伟，陈建峰.我国化工过程强化技术理论与应用研究进展[J].化工进展，2011，30(1):1-15.

[2] Jin Y，Cheng Y.Chemical Engineering in China:Past,Present and Future[J].American Institute of Chemical Engineers Journal，2011，57(3):552-560.

[3] Luo P C，Cheng Y，Jin Y，et al.Fast Liquid Mixing by Cross-flow Impingement in Millimeter Channels[J].Chemical Engineering Science，2007，62(22):6178-6190.

[4] 骆培成，程易，汪展文，等.液-液快速混合设备研究进展[J].化工进展，2005，24(12)：1319-1326.

[5] 孟辉波，王艳芬，禹言芳，等.射流混合设备内混合时间的研究进展[J].化工进展，2012，31(12)：2615-2625.

[6] 吴剑华.无搅拌混合装置：中国，CN 201110200231.3[P].2011-11-02.

[7] 鲁占军，杨春苹，高美蓉，等.浆料罐搅拌器改造总结[J].聚氯乙烯，2003(3)：44-45.

[8] Meng H B,Wang W,Wu J H,et al.Experimental Study on Instantaneous Pressure Fluctuation Time Series in the Novel Tank Agitated by Multiple Horizontal Jets[J].Chemical Engineering Research and Design,2012,90(11):1750-1764.

[9] Yu Y F,Wu J H,Meng H B.Numerical Simulation Process Aspects of the Novel Static Circulating Jet Mixer[J].Canadian Journal of Chemical Engineering,2011,89(3):460-468.

[10] 禹言芳，吴剑华，孟辉波.循环射流混合槽内瞬态压力波动非线性标度特性[J].过程工程学报，2012，12(5)：728-734.

[11] 禹言芳，吴剑华，孟辉波.基于局域波分解的循环射流混合槽内压力脉动信号时频特性分析[J].北京化工大学学报(自然科学版)，2012，39(6)：23-30.

[12] 禹言芳，吴剑华，孟辉波.新型循环射流混合器湍流特性分析[J].过程工程学报，2011，11(1)：1-8.

[13] Zughbi H D,Rakib M A.Investigations of Mixing in a Fluid Jet Agitated Tank[J].Chemical Engineering Communication,2002,189(8):1038-1056.

[14] Zughbi H D,Ahmad I.Mixing in Liquid-jet-agitated Tanks:Effects of Jet Asymmetry[J].Industrial and Engineering Chemistry Research,2005,44(4):1052-1066.

[15] Jayanti S.Hydrodynamics of Jet Mixing in Vessels[J].Chemical Engineering Science,2001,56(1):193-210.

[16] Patwardhan A W.CFD Modeling of Jet Mixed Tanks[J].Chemical Engineering Science,2002,57(8):1307-1318.

[17] 江帆,黄鹏.Fluent高级应用与实例分析[M].北京：清华大学出版社，2008:11-17.