大型风电场的最优无功控制
宋 洋,苏浩轩,邵 龙
(1.东北电力大学 研究生院,吉林 吉林132012;2.通辽供电公司,内蒙古 通辽028000;3.华北电力大学 电气与电子工程学院,河北 保定071003)
0 引言
随着风电技术的发展,在某些地区,风力发电所占的比重大大提高。这些风电场的接入将大大丰富我国的能源结构,为改善我国的环境条件,减少常规能源的消耗起到相当重要的作用。但同时,也需要看到风力发电对常规电力系统的不良影响。风机发电需要吸收一定的无功功率,当风电所占比重较大时,在风电场正常运行时就需要从电网吸收大量的无功,这就会造成电网的无功不足,导致电压水平的降低。所以,在大规模风电并网运行时,必须对无功功率进行优化控制,才能保证风电场的稳定运行。
用于无功优化的传统的方法有:非线性规划、混合整数规划[1,2]。最优非线性特性的无功功率问题存在几个局部最小值,基于导数方法的传统技术可能无法有效地获得这个问题的全局最小值。所以,近来基于人工智能或进化算法的新技术已经广泛使用。这些技术包括人工神经网络(ANN)、禁忌搜索(TS)、模拟退火(SA)、专家系统(ES)、遗传算法(GAs),差分进化(DE),进化编程(EP),粒子群优化(PSO)等[1,2]。其中,PSO 被认为优于其他类似的人工智能方法[3]。
在基于SCIG 的风电场中,主要通过控制电能损失和电压偏差来达到无功功率的最优分布[4~6],此外,本文提出第3 个目标函数,即SVC-RPR 最大化。将上述3 个目标函数整合成一个目标函数,并采用PSO 算法对所研究问题进行分析,得出无功功率的优化结果。
1 数学模型的建立
1.1 鼠笼型风机的数学模型
鼠笼式感应发电机(SCIG)由于其成本低、寿命长、结构简单、鲁棒性好和易于并网等原因在风电场经常使用[7]。
图1 显示了稳定状态下SCIG 的简化等效电路。Xs是定子漏抗,Xr是转子漏抗,Rr是转子电阻,Xm是励磁电抗,S 是转差率,V 是机端电压。在这个电路中,定子电阻可以忽略不计。

图1 SCIG 简化等效电路
从图1 中可以看出,SCIG 风力机的注入有功功率表示为

其中:X=Xs+Xr。
从图1 中还可以看出,阻抗jXm和是并联的。因此,等效阻抗可以表示为

对式(2)进行推导简化可得功率因数表达式如下:

风力发电机吸收的无功功率表示为

1.2 目标函数与约束条件
本文所进行的无功优化方法中,包括3 个目标函数:
第1 个目标函数是总功率损耗最小,如式(5):
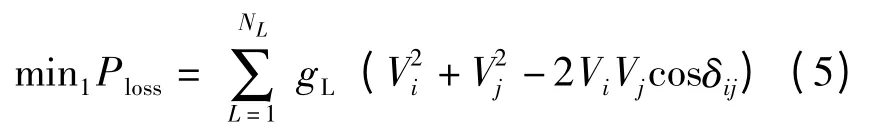
为了获得高质量的电压情况,要求平均负载电压偏离标称电压最小,即第2 个目标函数:

第3 个目标函数的二次形式表示如式(7):
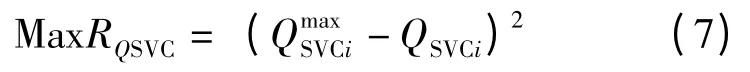
该优化方法需要满足的等式约束与不等约束为:
等式约束为有功、无功的平衡:

不等式约束分为以下3 个部分:
(1)状态变量的限制
这些都是同步发电机减去所有线路的负载电压、电压相角和无功功率输出节点的输出的约束条件:

(2)控制变量的限制
这些约束条件包括变压器的分接头位置、电容器和SVC 的容量、同步发电机的电压等级:

(3)固定变量的限制
风力发电机的功率极限:
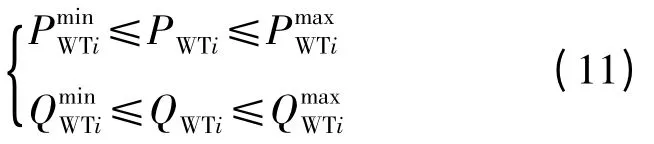
式中:Ploss是总有功功率损失。gL是线路电导。Vi,Vj,δi和 δj分别是目线i,j 的电压幅值及相角。δij是Vi和Vj之间的角度。NL和NB分别为线路和母线的数量。εV是平均电压偏差,VDi是母线i 的电压,Vi,nom是额定电压。GGi,WTi和QGi,WTi是 风力发电机发出的有功与无功功率。|Yij|是母线i,j 间导纳的大小,θij是其角度。PDi和QDi分别是母线i 的有功、无功需求。VGi发电机母线i 的电压幅值。QCi和QSVCi分别表示固定电容器和SVC容量,Ti表示变压器分接头位置。
2 算法介绍
PSO 可以有效地应用在许多非线性优化问题上。与许多传统的数学方法相比,这种优化方法不需要客观的梯度信息或误差函数,它可以独立得到最好的解决方案[8]。该方法也更少依赖初始点便可以得到全局最优解。
本文所采用的方法中,每个粒子更新速度为:

因此,这个新粒子的位置是:

将3 个目标函数加权为一个总的函数。为了处理这些约束,采用罚函数的方法。粒子F(Xi)这个问题为一个多目标罚函数,给出公式如下:

式中:Xi为粒子维度(等于变量的数目);ω1,ω2,ω3分别为有功损耗,电压偏差和SVC 无功储备3 个目标函数的权重。在3 个目标函数里,有功损耗是起到决定性作用的,故其所占的比重应该是最大的。另外电压偏差是关系到电能质量的重要指标,要满足电网安全稳定运行的硬性指标,所以其权重要大于SVC 无功储备的权重,在此理论指导下,通过大量的研究分析,分别取不同的权重组合进行计算,鉴于篇幅限制,这里对各种计算结果不予罗列。对各种权重的优化结果进行对比,最终选取ω1,ω2,ω3分别取0.7,0.2,0.1,取得最好的无功优化结果。
另外,P(Xi)的制定方法如下:
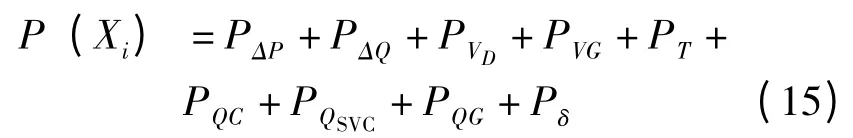
其中:
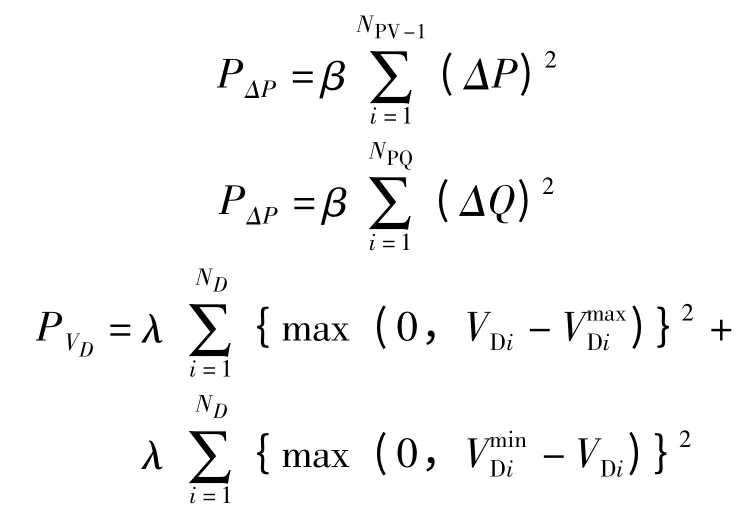

上述各式中,NPV-1是PV 节点的数目减去松弛节点的数目,NPQ是PQ 节点数,ND是负荷节点数,NT 是分接头可变的变压器数,NQc是固定电容器组的数量,NQSVC是SVC 的数量。β 和γ 是惩罚系数。
3 算例分析
采用Wale & Hale 6 总线系统进行算例研究。该算例系统有6 个节点,其中一个平衡节点,一个PV 节点。各个节点所带负荷以及节点间的联结参数如图2 所示。表1 中给出的是鼠笼式感应发电机数据。风电装机容量占整个负荷容量的45%。这意味着60 MW 的风电场(2.3MW ×26)连接到总有功负载为135 MW(线路3,线路5 和线路6)的网络中。例如,额定风电场输出功率(60 MW),吸收无功功率的计算便是30.49 MVar。所以,在风电场总线上安装一个容量为0~30.5 MVar 的SVC。
风电场输电线路和变压器的影响可以忽略不计。电力系统容量基准值为SB=100 MVA。

图2 Wale & Hale 6 总线系统

表1 2.3 MW 的SCIG 参数
本文进行了3 种不同情况下的分析研究,为了合理安排论文长度,所以没有给出最优控制和状态变量。
案例1:不投入SVC 且只考虑有功损耗的最优解
在这种情况下,该算法执行在未投入SVC 时且只考虑有功功率损耗一个目标函数。
案例2:投入SVC 且只考虑有功损耗的最优解
这种情况下需要在投入SVC 补偿装置后,且只考虑有功功率损耗一个目标函数。
案例3:考虑所有的3 个目标函数的最优解
这种情况下,综合考虑3 个目标函数(有功功率损失、电压偏差和SVC 无功储备)。
3 种情况下,总有功功率损耗、SVC 补偿容量和电压偏差分别如图3~5 所示。负荷电压最大最小值如表2 所示。
从图3 中可以看出,总有功功率损耗在使用SVC 后减少了。然而,由图4 可以看出,当只考虑有功损耗时,SVC 补偿容量投入最多才能达到尽可能减小有功功率损耗的目的。虽然有功损耗减少,但由表2 可知,其电压质量大大增加,表现为在图5 中平均电压偏差增加了。
在优化过程中当平均电压偏差和SVC-RPR 同时被考虑时,由优化结果可知,电压水平大大提高,SVC-RPR 也取得了最大值。但这是以有功功率损耗为代价实现的。

图3 不同风电场总有功功率最小输出损失

图4 不同风电场最优SVC 无功功率输出

图5 不同风电场线路负载电压输出平均最小偏差

表2 风电出力不同时的电压值
4 结论
本文基于鼠笼式感应发电机利用PSO 算法,对一个大型风电场并网系统中关于无功功率优化控制进行仿真计算。计算结果表明,一个风电并网系统中,对SVC 进行有效控制可以很好地改善电压分布,减少有功损耗并且能将SVC-RPR 最大化。然而,在风力发电出力较多时,由于3 个目标函数之间的冲突,很难得到一个充足的SVCRPR,除非SVC 的容量是按照SCIG 在满载时需要的无功功率容量来配置。
[1]Bakare G A,Krost G,Venayagamoorthy G K,et al.Differential evolution approach for reactive power optimization of Nigerian grid system[C].Tampa:IEEE Power Engineering Society General Meeting,2007.1-6.
[2]Zhu J.Optimization of power system operation[M].New Jersey:John Wiley & Sons,Inc.,2009.
[3]Venayagamoorthy G K,Harley R G.Swarm intelligence for transmission system control[C].Tampa:Power Engineering Society General Meeting,2007.1-4.
[4]Li L,Zeng X J,Zhang P.Wind farms reactive power optimization using genetic/tabu hybrid algorithm[C].Hunan:Intelligent Computation Technology and Automation,2008.1272-1276.
[5]Wei X,Qiu X,Xu J,et al.Reactive power optimization in smart grid with wind power generator[C].Chengdu:Power and Energy Engineering Conference,2010.1-4.
[6]Li L,Zeng,X J,Zhang P,et al.Optimization of reactive power compensation in wind farms using sensitivity analysis and tabu algorithm[C].Edmonton:Industry Applications Society Annual Meeting,2008.1-5.
[7]El-Helw H M,Tennakoon S B.Evaluation of the suitability of a fixed speed wind turbine for large scale wind farms considering the new UK grid code[J].Renewable Energy,2008,33:1-12.
[8]Zaraki A,Bin Othman M F.Implementing particle swarm optimization to solve economic load dispatch problem[C].Malacca:Soft Computing and Pattern Recognition,2009.60-65.
[9]Mantawy A H,Al-Ghamdi M S.A new reactive power optimization algorithm[C].Bologna:Power Tech Conference Proceedings,2003.
[10]李鸿鑫,李银红,李智欢.多目标进化算法求解无功优化问题的比较与评估[J].电网技术,2013,37(6):1651-1658.
[11]雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009.
[12]李智欢,段献忠.多目标进化算法求解无功优化问题的对比分析[J].中国电机工程学报,2010,30(10):57-65.
[13]邵龙,苏皓轩,王慧敏.大规模风电并网时双馈风机无功出力研究[J].电力科学与工程,2013,29(9):18-23.
[14]李辉,栗树林,包伟华,等.并网风电场电压稳定的无功补偿策略[J].电力科学与工程,2013,29(9):13-17.

