基于引力搜索算法的含分布式电源配电网重构
韦胜旋,刘前进,施 超,许慧铭
(华南理工大学 电力学院,广东 广州510640)
0 引言
配电网具有闭环设计、开环运行的特点。配电网重构是在满足系统正常运行允许的条件下,通过控制分段开关或联络开关的通断来改变馈线的拓扑结构,并保持网络的辐射状而没有孤立节点,实现减少功率损耗、提高可靠性、平衡负荷等目的[1]。分布式电源(Distributed Generator,DG)接入配电网已成为研究热点和必然趋势,大量DG 接入改变了配电网结构,会使配电系统的网损、电压分布、电压稳定性、短路电流等发生变化,这种变化与DG 的安装位置、容量直接相关。目前的DG 规划主要在网络拓扑结构不变的情况下选址和定容,为保证配电网时刻运行在最优状态,应根据网络结构的变化相应的调整可调度DG 的出力。
配电网络重构是一个复杂的多目标非线性整数组合优化问题,国内外学者对此进行了大量研究。文献[2]采用传统的启发式算法对配电网络进行重构求解,此类算法计算速度快,但一般只能得到次优解。为了获得最优解,文献[3]采用自适应遗传算法、文献[4]提出基于节点集的蜜蜂进化型遗传算法、文献[5,6]分别提出基于类电磁机制和基于全有效解整数微分进化算法的配电网重构。文献[7]考虑了不同类型DG 的影响,采用领域免疫搜索算法来寻优。文献[8]建立了含分布式电源的基于多种负荷方式的配电网重构模型,采用了二进制粒子群算法;文献[9]将基于多Agent 联盟机制的相关理论引入到含DG 配电网重构研究中。上述文献大多以降低网损为优化目标,较少涉及对系统供电可靠性的优化。在实际运行中,供电部门对供电服务越来越重视,因此在配电网重构中应该对网损及可靠性的影响。
本文提出以一种新的进化算法,引力搜索算法(Gravitational Search Algorithm,GSA)来解决含分布式电源的配电网多目标重构问题。它已被证明可以获得比粒子群算法更好的最优解[10]。多目标优化中各目标具有不同的量纲和数量级,因此引入隶属度对各目标进行模糊化处理,然后根据决策函数从帕累托前沿中择取最优解。对IEEE33 节点配电网络系统进行计算,比较分析了不同的优化方案和不同算法的运算结果,仿真结果验证了所提出模型和求解方法的正确有效。
1 含DG 配电网重构的数学模型
1.1 目标函数
(1)系统有功损耗
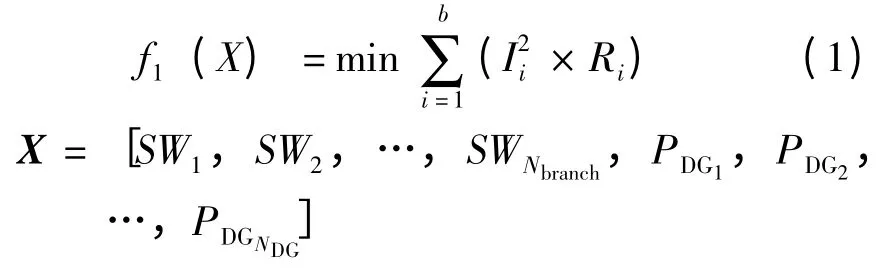
式中:Ii和Ri分别是第i 条支路的电阻和流过的电流;SWi是第i 条支路联络开关或分段开关的状态;Nbranch是带开关支路数,0 和1 分别表示开关断开和闭合;PDGi是第i 个功率可调DG 发出的有功功率;NDG为可调度DG 的个数。
(2)系统缺供电量
缺供电量是反应中低压配电网可靠性的重要指标。设一个配电网含有n(n >1)个节点,0节点代表源节点。其余节点为负荷节点,有功功率为Pi,i ∈(1,2,…,n- 1)。第i 节点的ENS 可以用式(2)计算[11]:
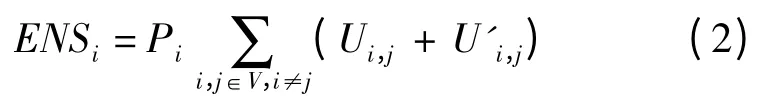
式中:Pi是节点i 的负荷的有功功率;V∈(0,1,…,n-1)表示配电网中各节点的支路的集合;Ui,j是所有与i 节点连接支路的与故障修复时间有关的可靠性参数;U'i,j是所有与i 节点连接支路的与故障定位时间有关的可靠性参数。Ui,j和U'i,j与下列因素有关[12]:

式中:λi,j和di,j分别是节点i 和节点j 之间支路的故障率和长度;ti,j和t'i,j分别是节点i 和节点j 之间支路的平均故障修复时间和平均故障定位时间。
例如,一个简单的配电网结构如图1 所示。对于节点3 的ENS,如果支路1 或支路2 发生故障,那么节点3 的停电时间为故障支路的修复时间;如果支路3 发生故障,那么节点3 的负荷的停电时间为故障定位和非故障线路合闸所需要的时间。因此,节点3 的ENS 为:
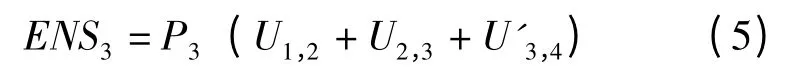
因此,整个系统的ENS 可以表示为:
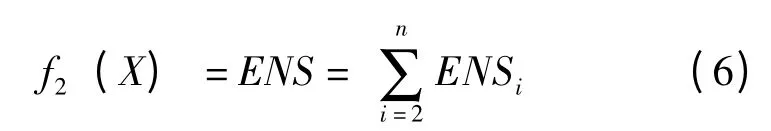

图1 简单配电网单线图
1.2 约束条件
配电网重构需满足以下约束条件:(1)拓扑约束:重构后的配电网必须为辐射状结构;(2)供电约束:配电网必须满足负荷的供电,不能有孤立节点;(3)电压幅值:各节点的电压不能超过正常运行允许的上下界,Vmin≤Vi≤Vmax;(4)支路容量:支路传输的实际功率不能超过其允许容量,Imin≤Ii≤Imax。
在配电网的潮流计算中,DG 一般可以建模为PV 节点或PQ 节点。当DG 被建模为PV 节点时,它必须吸收一定的无功功率来保持电压恒定。因此,在本文中采用DG 的PQ 模型来进行潮流计算。
2 改进引力搜索算法
简单介绍GSA 算法的流程如下。
假设在d 维搜索空间里有N 个粒子,第i 个粒子的位置为,根据牛顿引力定律,第i 个粒子受到第j 个粒子的作用力为:
式中:t 为算法的迭代次数;Maj为第j 个粒子的主动引力质量;Mpj为第j 个粒子被动引力质量;G(t)为引力时间常数,以下列方式更新:
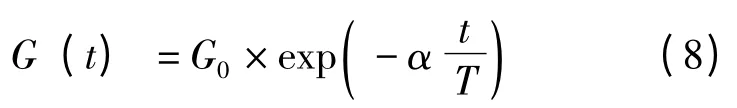
式中:G0为初始时刻引力常数,一般取值100;α一般取20;T 为算法最大迭代次数。
然后,计算粒子i 的适应度函数值fi(t),将第t 次迭代时的最优适应度和最差适应度分别记为Fbest(t)和Fworst(t),通过下式计算每个粒子的质量:
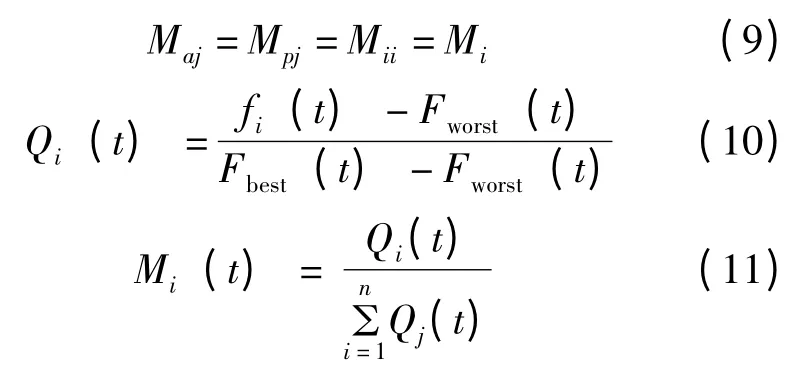
对第i 个粒子,受到来自其他粒子引力合力用引力的随机加权和表示为:

式中:rand1是介于0 到1 之间的随机数。
根据牛顿第二定律,粒子运动的加速度为:

那么,粒子运动速度及位置根据下式更新:
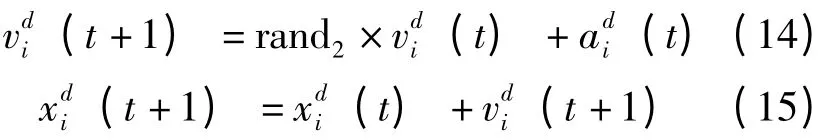
式中:rand2是介于0~1 之间的随机数。
GSA 算法与传统的PSO 算法相比,有以下优势:在粒子群算法中,粒子的运动方向仅与粒子个体极值Pbest和群体极值Gbest有关,而GSA 算法中,粒子的运动与所有粒子的合引力有关,这样可以有更高的收敛速度且不容易陷入局部最优。
3 多目标求解方法
3.1 模糊化处理多目标函数
在多目标函数的优化求解中,各子目标的相关性低甚至相互矛盾,要使多个子目标同时达到最优值比较困难。模糊集合理论以适当的隶属度函数,建立模糊集合,可以有效地处理优化过程中的不确定现象[13-14]。
多目标中的第i 个目标Fi的隶属度如下:
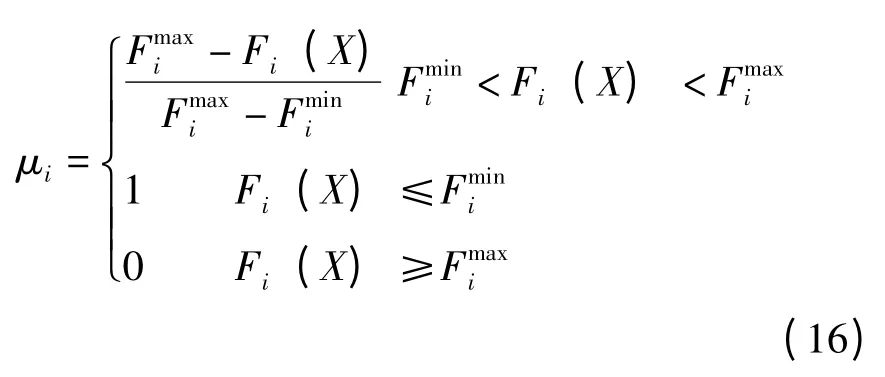
3.2 Pareto 最优解
本文运用Pareto 最优解理论来分析多目标优化的可行解之间的关系。Pareto 最优解理论是基于“支配”的概念,在多目标优化问题中,如果解X1和X2满足以下关系时,则称解X1支配X2。

式中:Nobj是优化函数中目标的个数。
3.3 模糊决策
在最终得到的Pareto 前沿中选取最具有实际工程价值的最优解,可以采用模糊决策的方法。将每次迭代计算获得的非支配最优解集综合起来,通过决策函数来择取最优解[15]。根据下式从非支配最优解集中选取最优解:
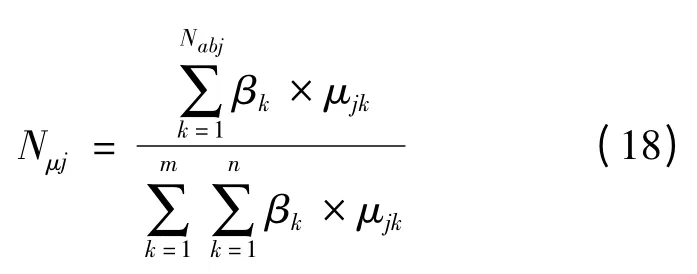
式中:Nobj是目标个数;βk是第k 个目标的权重;m 是非支配解的个数。
根据各目标的重要程度设置各目标的权重,选取具有最大隶属度函数值的Nμ作为最优解。
整个算法流程如图2 所示。

图2 引力算法搜索流程图
4 算例分析
为了检验本文提出方法的有效性,本文采用IEEE33 节点配电网络系统,系统结构图如图3 所示。图中,分支33~37 装设常开联络开关,其余分支装设分段开关。负荷、网络参数以及与系统ENS 有关的可靠性参数见文献[15]。
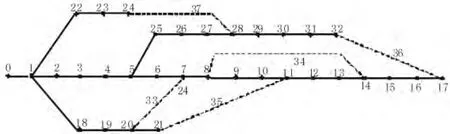
图3 IEEE33 节点测试系统图
通过优化计算,将以单目标和多目标的优化结果列于表1。从表1 中可知,分别以网损最小、ENS 最小以及综合考虑两种指标的配电网重构结果。当仅以有功网损最小为目标时,网损从201.24 kW 下降到138.04 kW,并且ENS 也明显降低。值得注意的是:仅以ENS 最小为优化目标时,网损反而比初始网络有所上升,并且开关操作次数为8 次。综合考虑两种优化目标时,算法搜索到的非劣解如图4 所示,图中非劣解构成了帕累托面。当两个优化目标的权重因子β1=β2=0.5,根据式(18)择取最优解列于表1 第3 行。可观察到网损和ENS 同时降低,表明优化算法取得了比较好的结果。
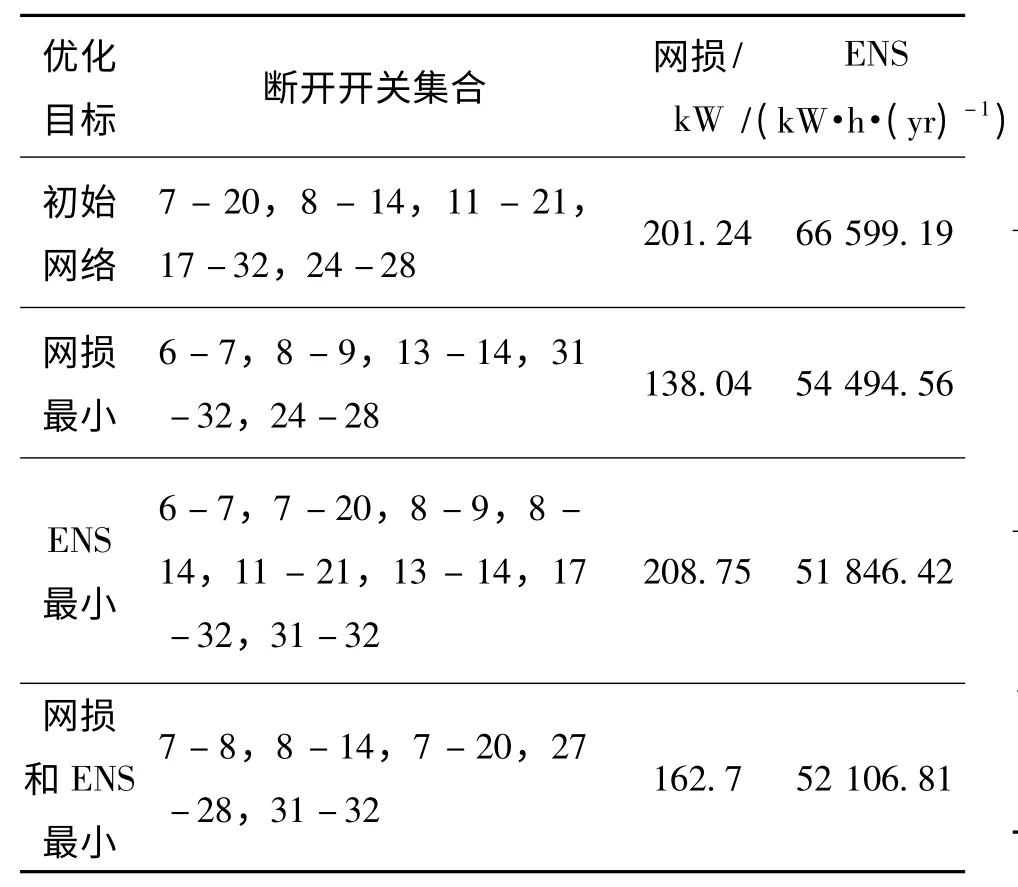
表1 以网损最小为目标的重构结果
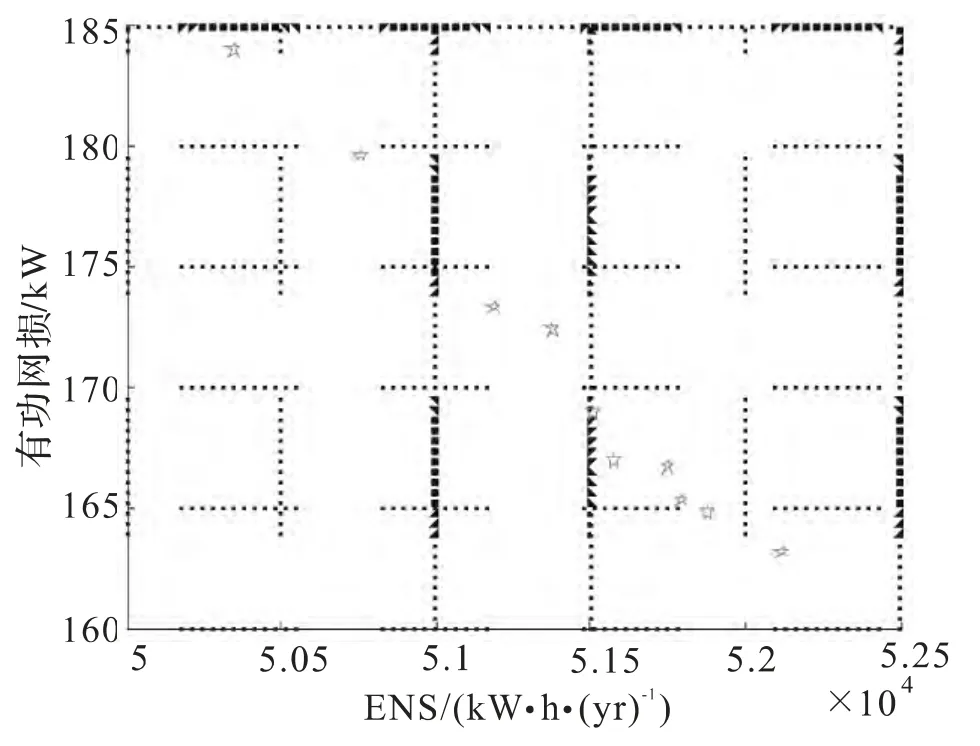
图4 非劣解空间分布
在算例原有基础上接入4 个DG,DG 的最大输出容量均为500 kW。其中,节点5 和节点15接入功率恒定类型DG,节点11 和节点30 接入功率可调类型DG。
接入DG 后配电网的优化重构结果如表2 所示。由表2 可知,经过配电网重构并优化可调度DG 的有功输出,可使网损相比于重构前大幅降低,ENS 显著下降。但是,当仅以降低网损或ENS 为优化目标时,势必引起另一目标值的恶化。因此,应当引入帕累托前沿来为实际运行提供足够的参考。可根据目标的重要性设置权重,本例中仍然设权重因子β1=β2=0.5,然后根据式(18)选取最优解列于表2 中。结果表明,网络重构后网损和ENS 值有较大幅度降低。通过配电网重构,并优化可调度DG 的有功输出,加入DGs的配电网达到了最优网架结构。

表2 以网损最小为目标的重构结果
为比较GSA 算法在复杂问题寻优过程的优势,图5 中给出了含分布式电源配电网优化重构、以网损最小为目标时,GSA 算法、PSO 算法和GA算法的收敛曲线。从图中可知,GSA 算法在5 次迭代之后即可达到最优解,收敛速度高于其他两种算法。
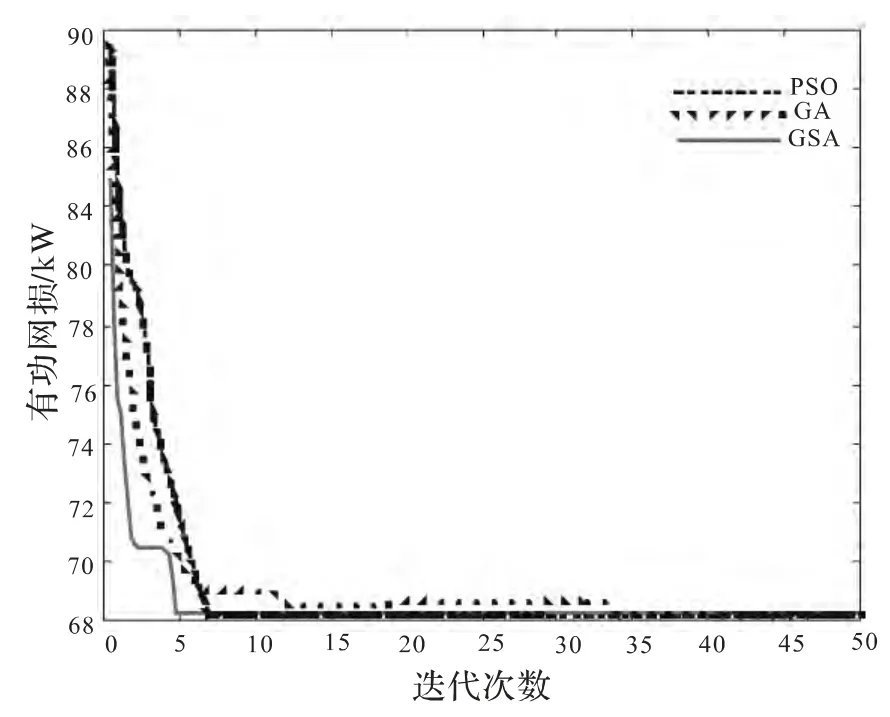
图5 IEEE33 节点测试系统
5 结论
本文以网损和缺供电量最小为目标,以开关组合以及分布式电源注入功率为控制变量,提出一种新的算法用于含分布式电源的多目标配电网重构。根据所获得的帕累托最优解,按目标权重因子利用模糊决策择取最优解。通过算例表明结果满足系统正常运行要求,并且具有较高的速度。
[1]邓桂秀,江修波,蔡金锭.基于混沌二进制粒子群算法的配电网重构研究[J].电力科学与工程,2013,29(9):34-37.
[2]González Alezeia,Echavarren F M,Rouco L,et al.A sensitivities computation method for reconfiguration of radial networks[J].IEEE Trans.on Power Systems,2012,27(3):1294-1301.
[3]许奎,杨波,李录兵,等.改进自适应遗传算法在配电网重构中的应用[J].电力科学与工程,2012,28(2):37-40.
[4]王超学,吕志奇,董慧,等.基于改进蜜蜂进化型遗传算法的含分布式电源的配电网重构[J].电力系统保护与控制,2012,40(15):52-56.
[5]李如琦,李芝荣,凌武能,等.基于类电磁机制算法的配电网重构[J].电力系统保护与控制,2012,40(14):116-120.
[6]曹文辉,彭春华,郭剑峰,等.基于全有效解整数微分进化算法的含分布式发电配网重构[J].电力系统保护与控制,2013,41(11):105-110.
[7]刘畅,黄民翔.含多种分布式电源的配电网重构优化研究[J].电力系统保护与控制,2013,41(6):13-18.
[8]刘宏江,李林川,张长盛.基于多种负荷方式的含分布式电源的配电网重构[J].电力系统保护与控制,2012,40(11):117-121.
[9]雷振,韦钢,言大伟,等.基于多Agent 联盟算法的含分布式电源配电网重构[J].电力系统保护与控制,2012,40(10):95-100,105
[10]Rashedi E,Nezamabadi-pour H,Saryazdi S.GSA:a gravitational search algorithm[J].Inf.Sci.,2009,179(13):2232-2248.
[11]Endreneyi J.Reliability modeling in electric power systems[M].NewYork:Wiley,1978.
[12]Càrcamo-Gallardo A,García-Santander L,Pezoa J E.Greedy reconfiguration algorithms for medium-voltage distribution networks[J].Power Delivery,IEEE Transactions on,2009,24(1):328-337.
[13]郭创新,游家训,彭明伟,等.基于面向元件神经网络与模糊积分融合技术的电网故障智能诊断[J].电工技术学报,2010,25(9):183-190.
[14]洪芦诚,石立宝,姚良忠,等.计及风电场发电功率不确定性的电力系统模糊潮流[J].电工技术学报,2010,25(8):116-122,130.
[15]Niknam T.An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration[J].Expert Systems with Applications,2011,38(3):2878-2887.

