考虑负荷不确定性的分布式电源的长期优化配置

罗振宇，陈家俊，周 勇，李渊博，邵 珂

(1．长春冰上训练基地，吉林 长春130000;2．长沙理工大学 电气与信息工程学院，湖南 长沙410004)

0 引言

分布式发电作为智能电网的重要组成部分，近年来受到日益广泛的关注［1］。国内外学者在分布式电源优化配置方面做了大量了研究。

文献［2］研究了分布式电源接入配电网以后综合目标函数的优化模型，包括电流、电压、投资成本，网损、谐波等指标为目标函数建立了一种新型的多目标优化模型。文献［3］基于多目标优化模型的分布式电源选址方案研究，利用多岛遗传算法进行求解，最后通过算例验证了算法的实用性和可靠性。文献［4］针对不同分布式电源发展阶段具有不同的投资主体，研究计及不确定性和多投资主体需求指标的分布式电源优化配置，使优化配置方案在整个发展阶段效益最优。文献［5］提出促进间歇性分布式电源的主动配电网的双层规划模型，能够得到更好综合效益。文献［6］考虑分布式电源处理的不确定，根据风光出力互补的特性，建立以有功网损最小为目标函数，这种方法与传统的方法相比能够提高分布式电源的利用率，但是这种规划方案，没有考虑到负荷不确定性。文献［7］通过改进的粒子群优化算法应用在分布式电源多目标优化求解问题中，虽然与传统的优化算法相比，提高了算法的收敛算法，但是不可避免易于陷入局部最优解，并且解的质量也不高。文献［8］提出多目标量子遗传优化算法应用到分布式电源选址和定容问题的求解中，建立了以有功网损最小为目标函数的优化模型，但是这种算法的参数设置复杂，并且运行速度慢。文献［9］中李明等人通过模拟细菌菌落生物机制，在2011 年提出细菌菌落优化算法，这种算法提供了一种新颖的循环结束方式，最后通过算例验证该算法具有很好收敛速度和精度。文献［10］将细菌菌落优化算法用在配电网的无功优化求解中，并申请了发明专利，同时也证明该算法在求解无功优化问题中，能够找到更高质量的解。

近几年来，对于分布式电源优化配置，一直是国内外学者研究的热点，但是目前大多数研究都是基于负荷不变的情形，在相关问题的模型和算法上面研究比较深入，很少有文献涉及到负荷的不确定性。但是，近期相关研究表明［11～15］负荷变化会改变节点负荷的电压和系统的网损。负荷的不确定性给分布式电源的优化和控制以及分布式电源位置和容量都发生变动。鉴于此，本文考虑负荷不确定性，建立了以有功网损为目标函数的优化模型，并且提出一种新颖的智能优化算法细菌菌落优化算法用在分布式电源优化问题的求解中，该算法原理简单，参数设置少，并且在没有任何外界条件的情况下，能够自行结束循环。

1 优化问题的建模

1.1 负荷不确定的模型建立

电力系统的规划分为长期规划和短期规划，长期规划是电网规划主要形式，但是在分布式电源的长期规划的时候，负荷一定会发生变化，而近期国内外的相关研究指出负荷的变化对电网的网损，电压稳定都有很大的影响，本文也通过相应算法验证了这一点，所以对于含有分布式电源的优化配置必须要考虑负荷不确定性，对于负荷变化的合理建模也至关重要。本文采用公式(1)对负荷的变化进行建模:

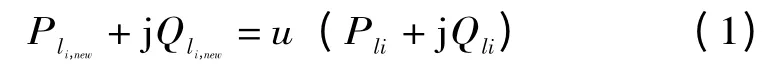
式中:u 为负荷的变化系数，范围0．5～1．5;i 为节点负荷。

1.2 目标函数模型的建立

1.2.1 数学模型的建立

本文以有功网损最小为目标函数，给出一个网损计算公式［16］:

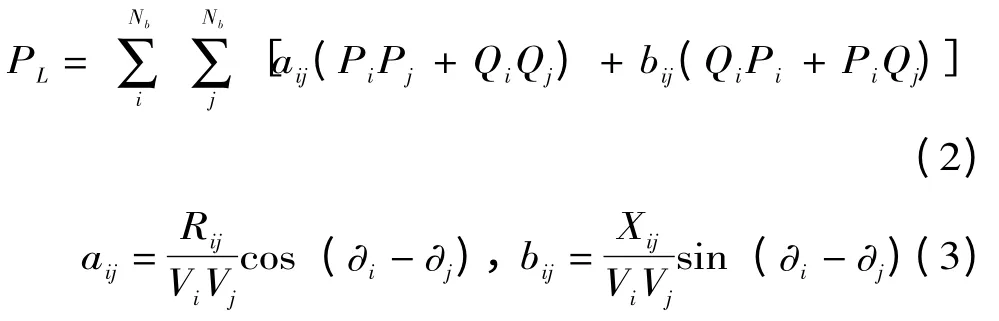
式中:Nb为线路的节点;线路的阻抗Zij=Rij+jXij。

1.2.2 约束条件

(1)等式约束

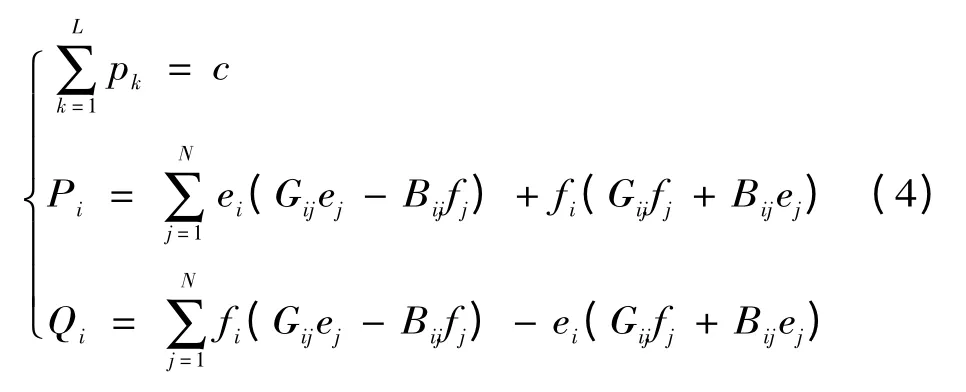
式中:L 为可以安装DG 的节点个数;C 为总的注入容量;Pi，Qi分别为节点i 的注入有功功率和无功功率;ei和fi分别为节点i 电压的实部和虚部;Gij，Bij分别为节点i，j 之间的电导、电纳。

(2)不等式约束条件

节点电压约束:

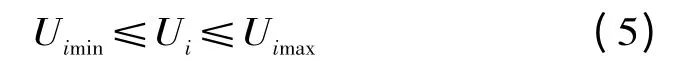
式中:Uimax，Uimin分别为节点电压的上下值。输电线路的传输功率极限约束为:

式中:Pij是节点i 到节点j 的传输功率。

2 细菌菌落优化算法

细菌菌落算法根据单个细菌的生长方式及其群体菌落生长演化过程来寻找最优解［17，18］。假设需要求解的优化问题用指定的培养液来表示，细菌培养液中营养物质的浓度表示为优化问题中对应的个体细菌的目标函数值(适应度的值)。细菌培养液中的营养物质不可能是无限的，细菌个体一定不可能无限制的繁殖下去，会受到营养物质和其他外界条件的一些约束，在优化算法中事先规定，菌落的种群最大的规模为N，细菌个体的繁殖数量不能超过规定最大规模N。

在适应阶段过了以后，根据外界的条件只要能够吸收充分的营养物质，细菌个体就能够繁殖，细菌个体就可以一分为二，相反当超过个体生命周期或者满足其他的一些规定条件时则死亡。由于细菌个体能够对于记忆外界的环境，保留其父代经历的最优位置，并且通过菌落信息相互沟通和交流可以保存整个菌落之前经历的最优位置。并通过这两个位置来影响细菌的位置的更新:细菌个体具有两种基本的运动方式:翻转和前进。前进即沿着上一次的转移方向向上面所讲述的两个最优位置移动，翻转即是在当前空间位置作随机运动。

在细菌个体的更新过程中，细菌个体所处的空间位置的目标函数值优于上一次位置的目标函数值时，细菌个体则会采取前进运动方式，细菌个体在前进的时候，空间位置的更新公式为:

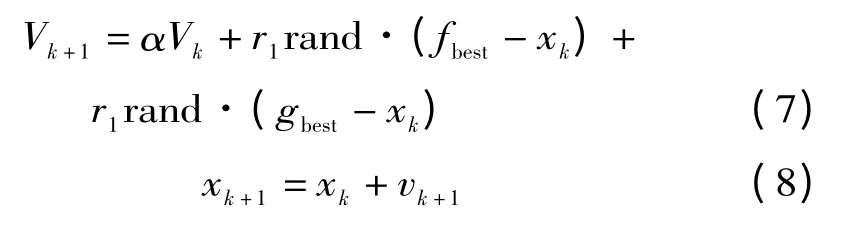
式中:Vk表示第k 次迭代时，个体前进的方向;xk对应的是第k 次迭代时，细菌个体在营养液培养基中的位置;fbest代表细菌个体上一次(父代)所经历的最优位置;gbest表示目前菌落所到达的最优位置;α，r1和r2为系数;Rand 为(0，1)上的随机数。

从式(7)和式(8)中不难发现，细菌个体位置更新公式与粒子群算法粒子更新公式很相似。其中就相当于粒子群算法中的粒子所经历的全局最优位置。但是他们两者之间的意义有很大的区别，在细菌菌落优化算法中fbest个体的数量会随着细菌个体的数目不断变化而增减。而在粒子群算法中，由于鸟的种群个数不会发生变化，所以相应的粒子个体所找到的最优位置的数目也不会有变化。

当个体所处的空间位置的目标函数值没有上一次的目标函数值优越的时候，此时就模拟了细菌个体在营养液中没有搜索到富集的营养物质的区域。此时细菌个体就会采取翻转的运动方式，即在附近的空间位置进行搜索。其位置的更新公式为:

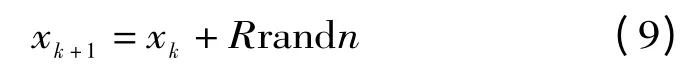
式中:R 是搜索半径;randn 为(-1，1)上的随机数。

可见细菌个体不仅会向营养物浓度高的区域前进，还有可能发生回退，或者是在前进和后退的路上徘徊。细菌个体在其生命周期N 中连续沿正的浓度梯度方向移动次数Np(N ＞Np)表示细菌个体吸收了足够的营养物质，可以进行繁殖了。否则认为细菌个体死亡。

根据达尔文生物进化论，生物的进化规律就是优胜劣汰，细菌经过一段时间的食物搜索过程后，达到繁殖条件的细菌个体进行自我繁殖，生成的新个体与原来的个体具有相同的位置，死亡操作即相应的个体消失。一般的智能寻优算法会采取迭代次数或者是搜索精度结束而伴随程序的结束，但是菌落算法根据自身仿生机制原理，当细菌菌落消失后算法就会自然结束，换句话说就是该算法可以在没有外界条件下，自行结束寻优算法程序。

3 算法流程

运用细菌菌落优化算法求解基于负荷不确定性分布式电源优化配置的步骤如下:

步骤1:分布式电源的容量在细菌菌落算法中对应于细菌在培养液中的位置，每一个细菌个体的搜索空间就是DG 的个数，然后代入算法进行优化。

步骤2:初始化一个细菌个体或者少量个体，设定种群的最大规模。

步骤3:设置系数u=0．5，在每一次的优化循环后自增0．01。

步骤4:计算细菌个体的目标函数值，根据初始化的细菌位置，调用潮流计算目标函数值，并记录当前的最优位置。

步骤5:如果细菌个体的目标函数值优越于父代，相应更新细菌个体的位置之后进行步骤(7)，否则进行步骤(6)。

步骤6:细菌个体翻转，判断是否达到死亡条件，达到则细菌个体死亡返回步骤(4)，否则直接返回步骤(4)。

步骤7:判断细菌种群的个数是否超过所设定的最大种群规模，没有则继续进行步骤(8)，否则，返回步骤(4)。

步骤8:判断个体满足繁殖条件，达到繁殖条件个体繁殖返回步骤(4)。

步骤9:判断细菌个体数量是否为0，为0 执行步骤(10)，否则返回步骤(4)。

步骤10:判断u 是否大于1 等于1．5，如果大于则结束循环，否则执行步骤(2)。

算法求解流程图如图1 所示。

图1 算法求解流程图

4 算例分析

本文采用IEEE33 节点作为仿真测试图［19］，对分布式电源的位置和容量进行确定和验证。该测试系统的接线如图2 所示，网络总负荷为3 715 kW+j2 300 kVar，电压基准值12．66 kV，平衡节点为0 号节点。

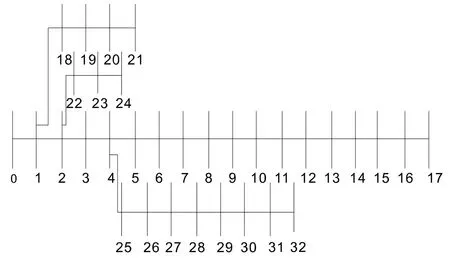
图2 IEEE-33 节点测试系统图

4.1 未接入分布式电源的情况

从上面的介绍可以知道，负荷在0．5～1．5 之间变化，每一次增加0．01，为了验证负荷的变化对于配电网有功网损、无功网损和电压影响，采用IEEE-33 节点做测试。

图3 反映了不同负荷水平下电压的变化情况。在图中可以看出负荷增加对于系统的电压产生较大的消极影响，当负荷增加50%时，此时节点的最小值在节点18，为0．848 01 p．u．，比负荷不变情况的最小值减少了6．8%左右。从图中还可以看出，当负荷减少的时候，电压有所增加，当负荷减少50%节点电压最小值也是在18 节点，为0．953 969，比负荷不变情况的最小值增加了6%左右。

图3 电压随负荷变化曲线图

有功和无功功率的随负荷变化，呈现离散状态，通过Matlab 二次拟合方法，有功功率和无功功率的变化在图4表现出来，从图形中可以分析出，随着负荷的增加，系统的有功网损和无功网损也在不断地增加，功率变化近似计算公式如下:

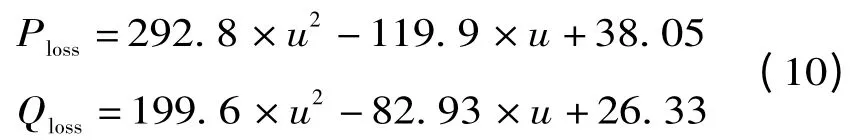
表1 考虑3 种负荷水平:基准负荷水平，增加50%的负荷水平，以及减少50%的负荷水平的情况下，节点电压以及功率变化值。

图4 网损随负荷变化的曲线图

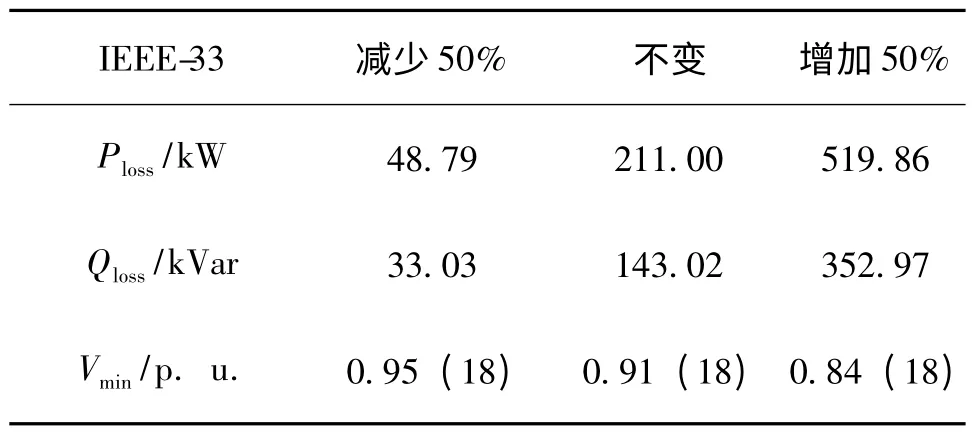
表1 没有接入DG 的3 种负荷水平下的电压和损耗

当节点负荷较少的时候，网络损耗有所增加，当增加50%，此时系统无功损耗和有功损耗增加了146%，146．85%;相反，当节点负荷减少时，配电网系统的功率有所增加，当系统的负荷减少到50%，有功功率和无功功率分别减少了76．87%，79．9%。

从上面的分析可以得知，负荷的变化对于配电网的电压和网损都有很大的影响，当负荷增加的时候，节点电压的值明显减少，但是网损的值却明显增加，当负荷减少的时候，节点电压有明显提高，当时网损的值却明显减少。

4.2 接入分布式电源情况

本文以逆变器型DG 做仿真验证，其中逆变器型DG 采取定PV 控制，功率因数为0．9，负荷的变化方式和4．1 节相同，初始参数设置如下:菌落的种群的最大规模设置为S=20，细菌个体生长周期设置为N=4 以及繁殖条件是Np=2，死亡条件Nr=2。参数设定α=0．7，r1=r2=1．5，搜索半径R 设置为10-1。为了验证算法的有效性，将优化的结果与粒子群算法进行比较，粒子群算法的参数设置［16］为:C1=C2=0．2，V=0．4。

4.3 结果分析

随着负荷的变化，以网损最小目标函数的分布式电源的优化配置接入位置并没有发生变化，两种算法的优化结果均是在6 节点接入分布式电源，不过优化结果容量却发生了很大变化，当负荷不断增加的时候，分布式电源接入的容量也在不断呈离散形态增加。

本文采取Matlab 曲线拟合技术得到两种优化算法的分布式电源接入容量近似的计算公式为:

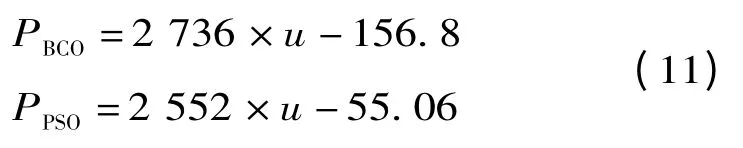
从图5 可以看出，分布式电源加入的容量随着负荷变化线性增加，但是负荷的变化并没有对分布式电源加入的位置产生影响，两种算法的优化结果都是分布式电源接入6 节点，本文所提算法收敛精度比粒子群算法精度要高，能够寻找到更精确的全局最优值，同时由于本文算法原理简单，便于理解，能够用在复杂问题的优化模型中。

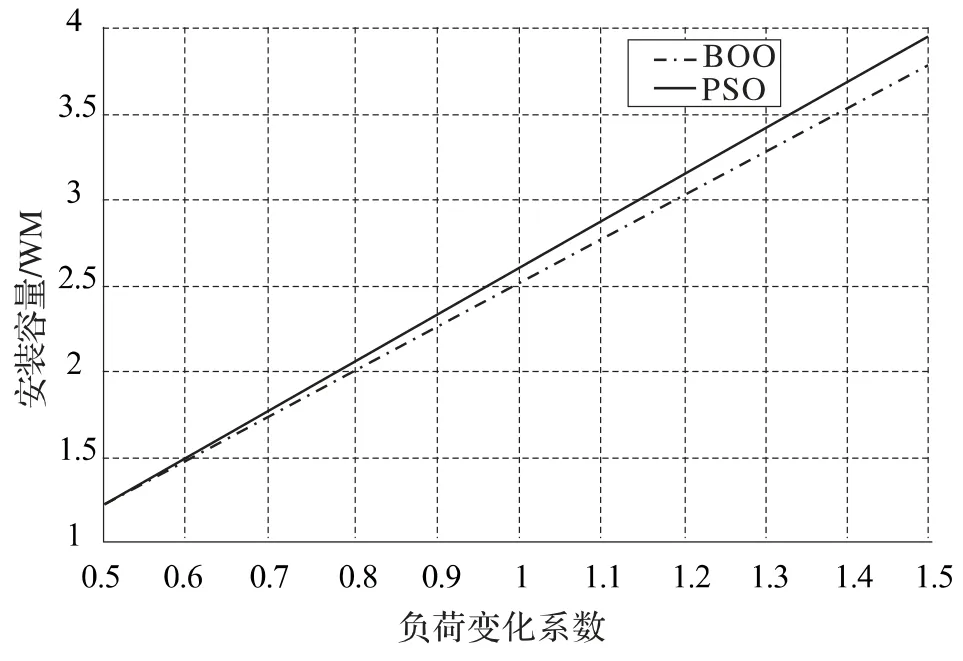
图5 分布式电源接入配电网的容量曲线

分布式电源接入以后，可以减少配电网网损改善电压质量，从上文的分析中可以得出，节点电压随着负荷变化而变化。

从图6 可以看出，接入分布式电源以后，节点电压有明显的改善。

表2 是未接入DG 和接入DG 以后节点电压随负荷变化情况，为了与上文作对比，仍然取3 种负荷水平电压作为比较对象。

图6 接入分布式电源之后电压随着负荷变化

表2 接入DG 之后3 种负荷水平下的电压和损耗

从表1 和表2 中可以分析出，分布式电源接入以后，考虑到负荷的不确定性，可以明显地改善由负荷变化引起的电压减少。

图7 接入分布式电源优化之后，在负荷不确定情况之下有功和无功网损变化曲线图。

图7 安装分布式电源之后网损随负荷变化

表3 是在3 种负荷水平下，分布式电源接入和接入之后的电压和网损的对比。

表3 接入DG 前后3 种负荷水平下电压和损耗对比

从表3 可以看出在本文负荷变化的模型，接入分布式电源以后电压和网损随着负荷变化比没有接入分布式电源有所好转。

5 结论

本文提出基于有功网损最小分布式电源长期优化配置的模型，对于负荷不确定性的处理，采用长时间的线性同步增长模型。首先，通过IEEE-33节点验证负荷变化对于电压和系统网损影响。然后在分布式电源优化配置过程让负荷线性变化，同时提出了一种新颖的智能仿生算法细菌菌落优化算法，该算法初始种群数目少，计算效率高，并且能够自行结束循环。最后通过算例，验证了所提模型的实际意义和本文算法适应性和更好地鲁棒性。

［1］裴玮，盛鹍，孔力，等．分布式电源对配网供电电压质量的影响与改善［J］．中国电机工程学报，2008，28(13):152-157．

［2］夏澍，周明，李庚银．分布式电源选址定容的多目标优化算法［J］．电网技术，2011，35(9):115-121．

［3］任洪伟，韩丛英，裴玮，等．基于多目标优化模型的分布式电源选址方案研究［J］．电力系统保护与控制．2013，41(24):64-69．

［4］江知瀚，陈金富．计及不确定性和多投资主体需求指标的分布式电源优化配置方法研究［J］．中国电机工程学报，2013，33(31):34-42．

［5］曾博，刘念，张玉莹，等．促进间歇性分布式电源高效利用的主动配电网双层场景规划方法［J］．电工技术学报，2013，28(9):155-163．

［6］邓威，李欣然，李培强，等．基于互补性的间歇性分布式电源在配网中的优化配置［J］．电工技术学报，2013，28(6):216-225．

［7］苏海锋，张建华，梁志瑞，等．基于LCC 和改进粒子群算法的配电网多阶段网架规划优化［J］．中国电机工程学报，2013，33(4):118-125．

［8］王瑞琪，李珂，张承慧，等．基于多目标混沌量子遗传算法的分布式电源规划［J］．电网技术，2011，35(12):183-189．

［9］Li Ming．A novel swarm intelligence optimization inspired by evolution process of a bacterial colony［J］．Proceedings of the 10th World Congress on Intelligent Control and Automation Beijing，China，2012:50-53．

［10］简献忠，周海，李莹，等．电力系统无功优化细菌菌落算法［P］．中国专利．201310140845．6，2013．04．02．

［11］Hung Duong Quoc，Mithulananthan N．Multiple distributed generator placement in primary distribution networks for loss reduction［J］．IEEE Transactions on Industrial Electron TCS，2012，60(4):1700-1708．

［12］王建学，高卫恒，别朝红．冲击负荷对电力系统可靠性影响的分析［J］．中国电机工程学报，2011，31(10):59-65．

［13］谢开贵，肖畅．计及负荷不确定性的无功优化模型与算法［J］．电力系统保护与控制，2011，39(4):18-22．

［14］刘莉，王刚，翟登辉．k-means 聚类算法在负荷曲线分类中的应用［J］．电力系统保护与控制，2011，39(23):65-68．

［15］刘健，武晓朦，余健明．考虑负荷不确定性和相关性的配电网络重构［J］．电工技术学报，2006，21(12):54-59．

［16］Krueasuk W，Ongsakul W．Optimal placement of distributed generation using particle swarm optimization［C］．Singapore:2010 2nd Internatioral confevence on Mechanical and Electrcal Technology(ICMIT)，2010．342-346．

［17］李明，杨成梧．细菌菌落优化算法［J］．控制理论与应用，2011，28(2):223-228．

［18］宋德逻，孔德福，李明．一种离散细菌菌落优化算法研究［J］．软件导刊，2013，12(12):52-54．

［19］Moradi M H，Abedini M．A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems［C］．Singopore:Internationd power and Energy conference．2010 Comference proceadings，2010:858-862．