三相PWM 整流器的鲁棒反演控制器设计

吴桂良，田永贵，李小明，程颖菲

(1．西南交通大学 电气工程学院，四川 成都610031;2．西安铁路职业技术学院，陕西 西安710014)

0 引言

以脉宽调制(PWM)控制为基础的各类变流装置在国民经济各个领域中已取得广泛应用。其在高压直流输电、有源电力滤波器、超导储能、交流传动等领域的研究应用一直是学术界关注的热点［1～6］。对其合理建模与深入研究控制策略具有重要意义。

反演法又称后退法、回退法，因其独特的构造性设计过程和对非匹配不确定性的处理能力，在控制系统设计中得到了成功应用［7］。反演控制的基本思想是将复杂的非线性系统分解成不超过系统阶数的子系统，然后为每个子系统设计部分Lyapunov 函数和空间虚拟控制量，一直后退到整个系统。反演法适用于可以状态线性化或具有严格参数反馈的不确定非线性系统。

对实际对象的数学建模不可避免带有未建模态、近似参数等不确定因素。不确定性的存在使实际对象与所用数学模型之前存在差别，仅根据标称系统设计控制器，会使大量工程控制问题无法获得满意结果，甚至严重影响系统性能［8］。鲁棒控制理论就是针对系统的不确定性的存在而提出的，它的优点在于抑制干扰和补偿未建模动态。

本文考虑到PWM 整流器在实际运行中存在的参数不精确的情况，建立包含不确定性的数学模型。采用反演设计法设计该系统的控制器，同时考虑到不确定性对系统性能的影响，引入鲁棒控制项对该影响进行补偿，增强系统的鲁棒性。应用Lyapunov 稳定性定理证明该系统为渐进稳定。在Matlab 中搭建仿真模型，验证所设计控制器的有效性。

1 三相VSR 暂态数学建模

三相VSR 拓扑结构如图1 所示。

图1 三相PWM 整流器拓扑结构

根据电路关系列写电流微分方程，并经Park变换后可得到下式［9］:

式中:id，iq为交流侧电流的d，q 分量;sd，sq为单极性二值逻辑开关函数;usd，usq为电网电压的d，q 分量;RL为负载等效阻抗，其余符号含义见图1。

交流侧与直流侧的有功功率分别为:

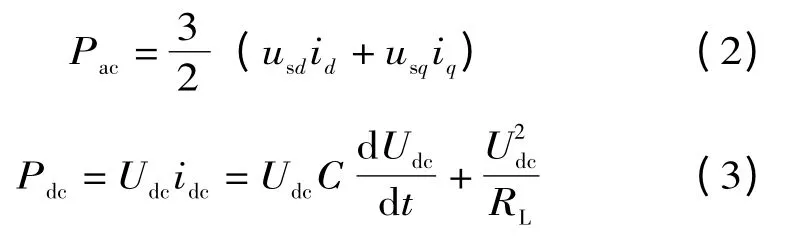
当忽略三相桥的自身损耗时，交流侧与直流侧的有功功率相等，联立式(2)、(3)并化简，可得:

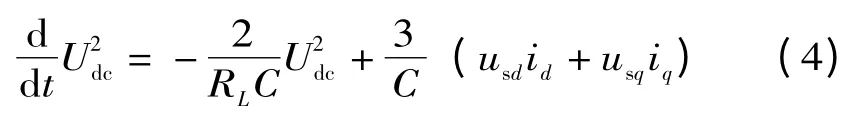
定义新变量u，并令

VSR 交流侧输出电压的d，q 分量vd，vq为

定义新变量ud，uq，并令

将式(5)、(7)代入(1)、(4)，可得三相VSR 在dq 坐标系中的数学模型

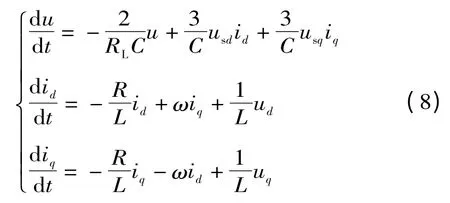
对于新变量u，ud，uq，式(8)为一组线型微分方程。

在实际系统中，受VSR 运行状态改变等因素的影响，R，L，RL这些参数通常不能精确测定。考虑它们的偏差为ΔR，ΔL，ΔRL，从而将系统模型(8)改写为(9)式。

定义x1=u，x2=［idiq］T，μ=［uduq］T，则可得到VSR 的不确定模型:

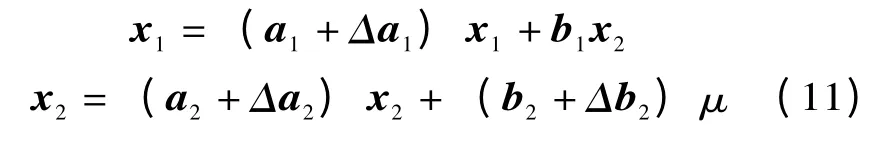
2 控制器设计与稳定性分析

为消除不确定性对系统的影响，保证在所有信号有界的前提下，系统状态指数收敛至系统远点的某一任意小的领域，对该系统设计一个鲁棒反演控制率。按照反演控制的设计方法，定义虚拟状态和虚拟控制，并在虚拟控制和实际控制中引入一个鲁棒项，以克服不确定的影响。

引入新的误差状态向量z1，z2［10］，

式中:x1d，x2d为系统期望的状态轨迹。对z1，z2求导可得状态误差的动态方程为

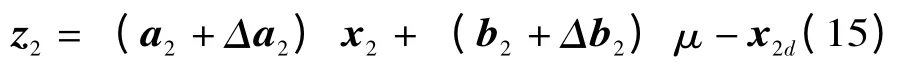
以下分两步进行控制器设计。

第一步:将系统式(14)重写为以下形式

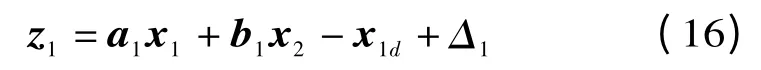
式中:Δ1为因参数不精确的影响而引入的不确定项，将通过引入一类鲁棒函数来补偿这种不确定性的影响。

假设1 存在一个未知的正数ρ1，使得

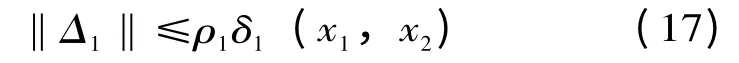
其中，δ1(x1，x2)为已知的非负光滑函数。

将x2看做子系统(16)的虚拟控制量，并在x2d中引入鲁棒控制项v1［11］来消除不确定性的影响，选取期望的虚拟控制量为

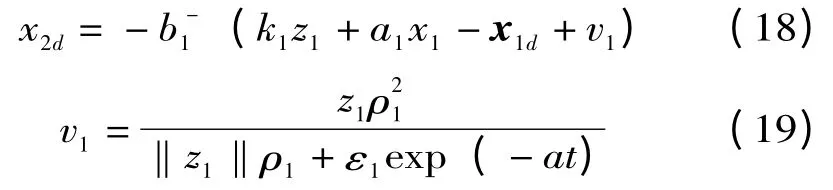
其中，k ＞0，ε1，a ＞0 为设计参数，为b1的广义逆。

选取Lyaponuv 函数

沿(16)式的方向对其求导可得:

第二步:重写(15)为

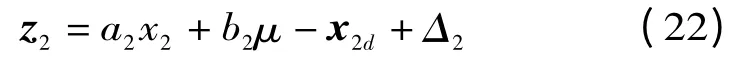
假设2 存在一个未知的正数ρ2，使得

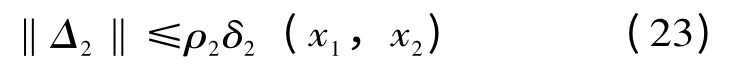
其中，δ2(x1，x2)为已知的非负光滑函数。

同理，取

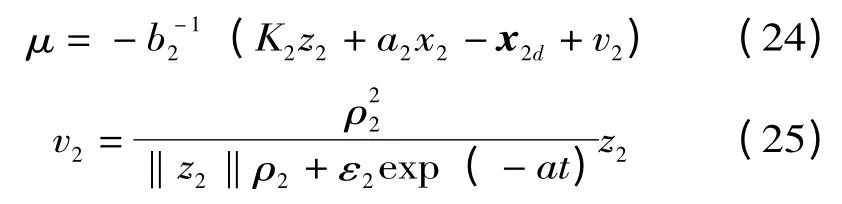
其中，K2=diag(k21，k22)，k21，k22＞0，ε1，a ＞0 为设计参数。

式(24)即为控制器的输出方程。

选取Lyaponuv 函数

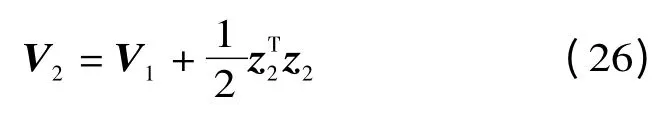
对(26)式求导可得:

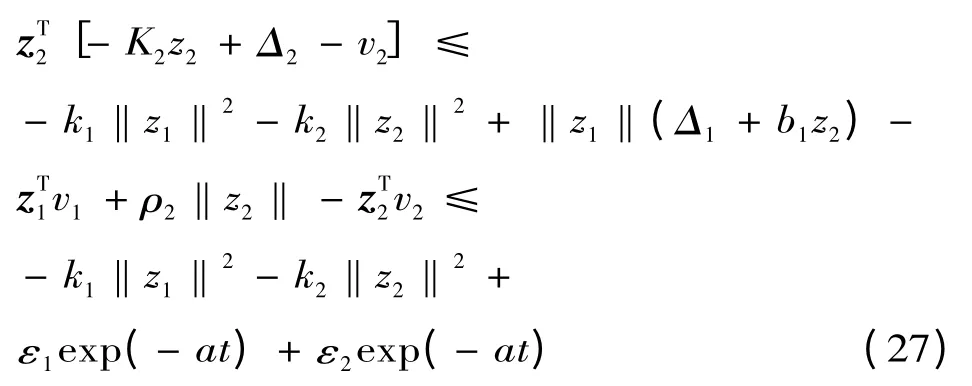
由Lyaponov 稳定性分析可知该系统为渐进稳定［13］。由此可设计鲁棒反演控制器如图2 所示。

图2 鲁棒反演控制器结构

3 仿真

为验证控制器性能，在Matlab/Simulink 中搭建如图3 所示的仿真模型。选取系统参数为RL=50 Ω，R=0．1 Ω，L=0．01 H，C=3 mF，交流侧电压usa，b，c=240 V，直流侧电压Udc=500 V，并假设参数误差＜30%。选取设计参数k1=45，k2=diag［93，93］，ε1=0．3，ε2=0．5，ρ1=3，ρ2=5，a=0．01。

图3 三相整流器仿真模型

在0．3 s 时，系统交流侧发生A 相单相接地短路，接地阻抗为1 mΩ，0．35 s 时故障切除，系统恢复正常运行。仿真结果如图4 所示。

图4 仿真波形图

由图4 可见，0．3 s 时系统发生短路故障，各变量发生小幅震荡，在0．35 s 时短路故障解除，各状态量可在短时间内恢复至正常运行状态，表明控制器可有效跟踪基准值，跟踪速度较快，跟踪误差较小。仿真结果表明，当选取合适的设计参数时，系统可正常运行并具有良好的动态性能。证明控制器具备良好的动态品质与跟踪性能。

4 结论

本文采用反演的控制方法对含有不精确参数的PWM 整流器设计非线性控制器，并在控制项中引入鲁棒控制项以补偿系统不确定性的影响。在Matlab/Simulink 平台下搭建仿真模型对所设计控制器性能进行验证。仿真结果表明，在正确选择设计参数下该系统具备良好的动态性能与跟踪性能。

［1］李正熙，王久和，李华德．电压型PWM 整流器非线性控制策略综述［J］．电气传动，2006，36(1):9-13，27．

［2］冯阳，王奔，王亚芳，等．有源滤波技术在串级调速中的应用［J］．电力科学与工程，2013，29(12):23-30．

［3］Sharma S，Singh B．An enhanced phase locked loop technique for voltage and frequency control of stand-alone wind energy conversion system［C］．New Delhi:2010 India International conference on Power Electronics(IICPE)，2011:1-6．

［4］燕跃豪，鲍薇，李光辉，等．基于混合储能的可调度型分布式电源控制策略［J］．华北电力大学学报(自然科学版)，2014，41(2):28-35．

［5］郭文勇，赵彩宏，张志丰，等．电压型超导储能系统的统一直接功率控制方法［J］．电网技术，2007，31(9):58-63．

［6］Marcos C，Sanchez-pena J M，Towes J C，et al．Note:Phase-locked loop with a voltage controlled oscillator based on a liquid crystal cell as variable capacitance［J］．Review of Scientific Instruments，2011，82(12):126101-126103．

［7］Kokotovic P．Constructive nonlinear control:Progress in the 90's［C］．Beijing，China:Proceedings of IFAC 14nd World Congress，1999，1:49-77．

［8］乔继红．反演控制方法与实现［M］．北京:机械工业出版社，2012．

［9］张兴，张崇巍．PWM 整流器及其控制［M］．北京:机械工业出版社，2013．

［10］胡云安，晋玉强，李海燕．非线性系统鲁棒自适应反演控制［M］．北京:电子工业出版社，2010．

［11］Yeong-Jeu，S．，L．Chang-Hua and H．Jer-Guang，Global exponential stabilization for a class of uncertain nonlinear systems with control constraint．Automatic Control，IEEE Transactions on，1998．43(5):674-677．

［12］伊西多．非线性控制系统(第三版)［M］．王奔，庄圣贤．北京:电子工业出版社，2012．

［13］过希文，王群京，李国丽，等．永磁球形电机的自适应反演滑模控制［J］．南京航空航天大学学报，2014，46(1):59-64．