输入不平衡时双级矩阵变换器的比例谐振控制

肖儿良，莫 康，陈朱杰

(上海理工大学 电气工程系，上海200093)

0 引言

双级矩阵变换器(Two Stage Matrix Converter，TSMC)是一种新型交—交变换器，省去了传统交直交变换器的中间直流环节，具有能量双向流动、功率因数可调、输出谐波低等优点［1］。在风力发电、变频调速等应用领域有很大的发展潜力。

由于TSMC 没有中间直流环节［2～5］，这使得输入侧的电网电压扰动会直接影响输出电流波形的质量，而且输出电流波形的畸变又可以通过双向开关传递至输入侧，引起电流波形恶化，从而导致电网侧电能质量下降［6］。因此研究非正常工况下的控制方法，是十分必要的。

近年来，国内外许多科研工作者对两电平和三电平TSMC 做了许多研究，三电平TSMC 比两电平TSMC 有更加优越的输出性能［7］，文献［7～9］针对三电平TSMC 的拓扑结构和控制策略做了研究，提出了几种新型的三电平TSMC 的拓扑结构。其逆变级的控制策略采用虚拟空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)方式，计算较为复杂，没有针对不平衡输入条件下的工作情况做进一步研究。为了改善在不平衡输入条件下输出电能的质量，文献［10］提出一种两电平Z—源TSMC 对中间直流环节进行自适应调节。但该新型电路拓扑是以引入储能元件为代价的。文献［11］提出一种基于广义预测的MC 电流环控制方案。文献［12］通过改变拓扑结构提出了一种三相四桥臂的TSMC，上述文献的研究思路和方法对于抑制不平衡输入的影响具有一定参考价值。

本文针对三电平TSMC 网侧电压输入不平衡情况，提出三电平矩阵变换器的比例谐振的控制算法。利用PR 控制器能够在αβ 静止坐标系下对交流信号无静差跟踪的优势，抑制不平衡输入对输出性能的影响，同时降低输出电流的谐波含量。提升三电平双级矩阵变换器的性能。

1 三电平TSMC 控制策略

图1 是三电平TSMC 的拓扑结构，它由3 部分组成:输入滤波器、整流级和逆变级。滤波器由电感和电容组成，整流级采用双向开关管，逆变级采用级联三电平中点钳位(NPC)变换器。图1 中p，n 分别为中间直流环节的正极和负极。三电平TSMC 的空间矢量调制分为整流级调制和逆变级调制两部分。

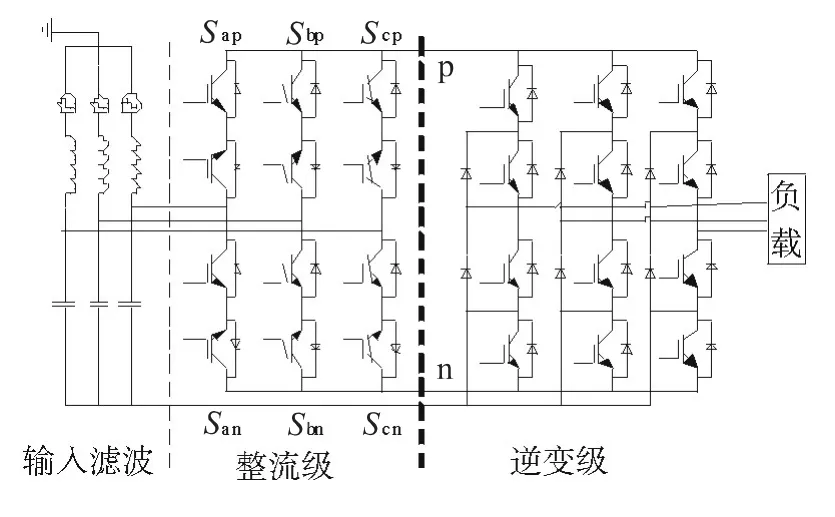
图1 三电平TSMC 的拓扑结构

1.1 整流级控制策略

假定输入三相电源电压为:

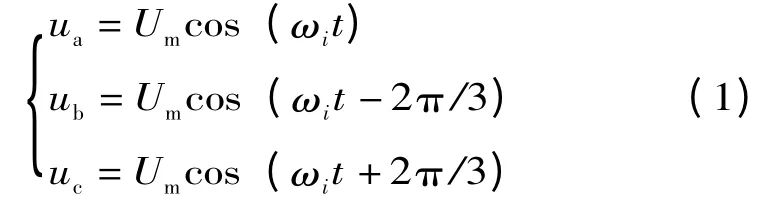
式中:ωi为输入角频率;Um为输入电压幅值。整流级采用无零矢量空间矢量调制，把输入相电压按周期分成6 个区间，如图2 所示。图中Son表示导通开关，Smod表示调制开关，Vdc表示中间直流电压。

图2 整流级开关状态

以0～π/6 区间为例说明，在这个区间内，ua极性始终为正且绝对值最大，ub，uc极性为负。此时Sap保持导通，Sbn，Scn按照开关状态轮流导通，从而在整流级输出侧获得尽可能大且极性为正的直流电压。由其导通方式可知中间直流侧的电压Vdc由线电压uab，uac和整流级开关状态决定。设中间直流侧平均电流为，则有

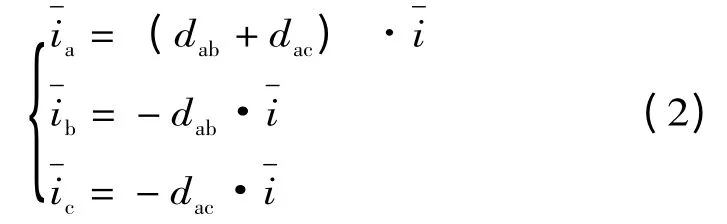
式中:dab+dac=1，dab，dac分别为线电压uab，uac对应占空比。

为了在不同的负载条件下输出功率因数为1，占空比dab，dac应该满足如下条件:

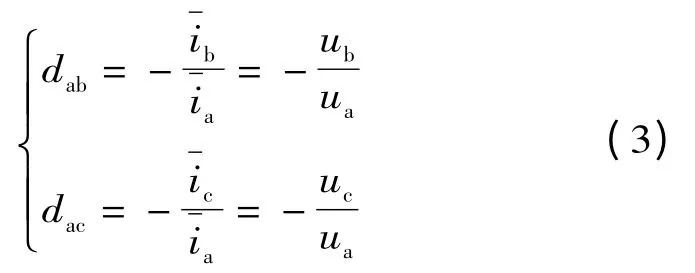
一个PWM 周期Ts 内的局部平均直流电压为

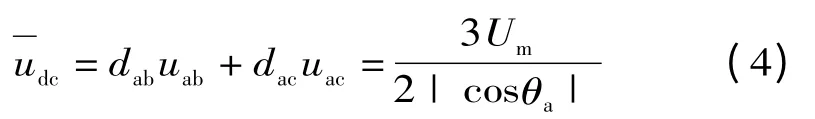
1.2 逆变级控制策略

逆变级采用级联三电平中点钳位(NPC)变换器。调制方式采用一种基于60°坐标系的SVPWM 算法，该算法不需要大量的三角函数运算，计算简单、快速、易于实现［13］。

基于60°坐标系为g-h 坐标系，取水平轴为g轴，再将g 轴逆时针旋转60°为h 轴。g-h 坐标系与α-β 坐标系坐标变换公式为

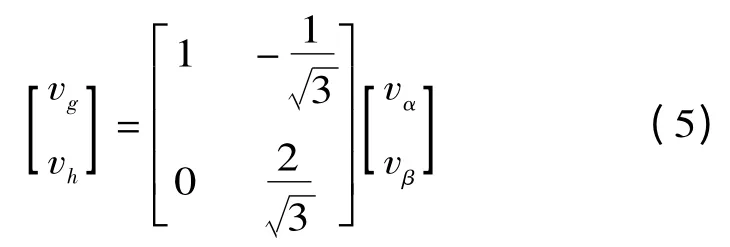
由Clark 变换可以得到a-b-c 坐标系与g-h 坐标系之间的变换公式为

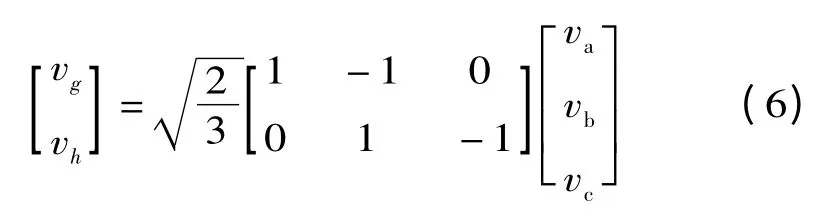
图3 为60°坐标系下三电平空间矢量图。在图3(a)中将空间划分为6 个大区，其中每个大区又分为4 个小区如图3(b)所示。

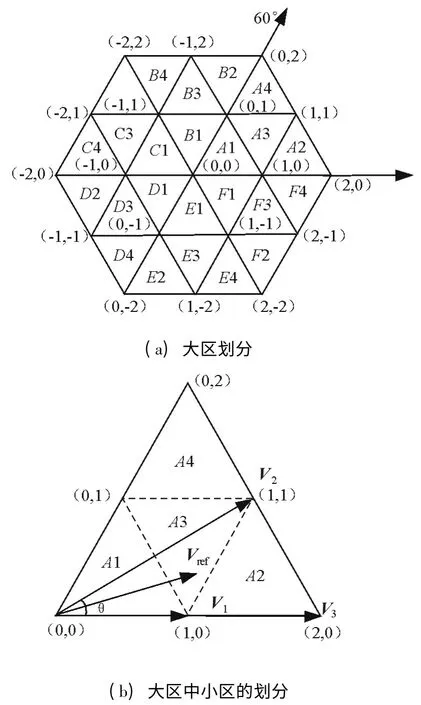
图3 60°坐标系下三电平空间矢量图

表1 和表2 分别为大区和小区的分区规则，通过表中简单的算术逻辑运算就可以确定任意矢量Vref(vrg，vrh)所在的区域。

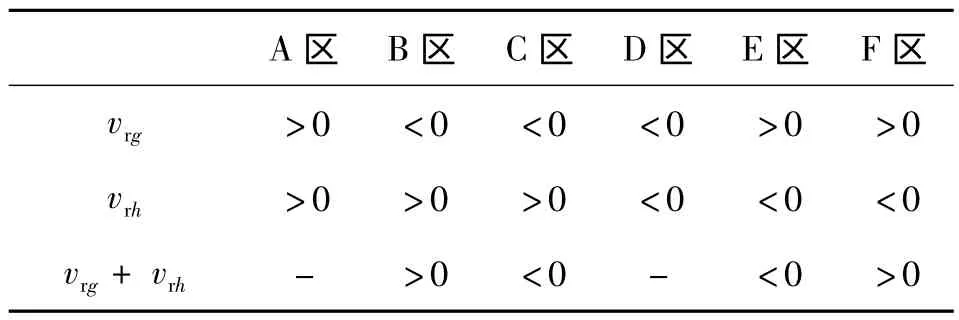
表1 大区的分区方法

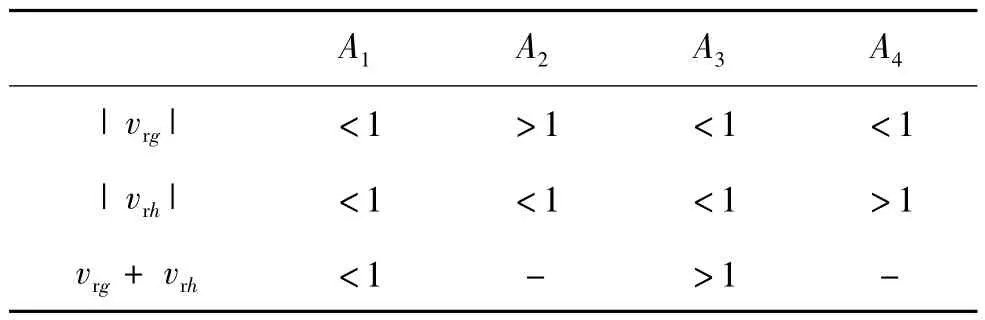
表2 A 区中小区的分区方法

对于一个给定的参考矢量Vref(vrg，vrh)如图3(b)，可以由最近三矢量合成得到，各个矢量的占空比公式为

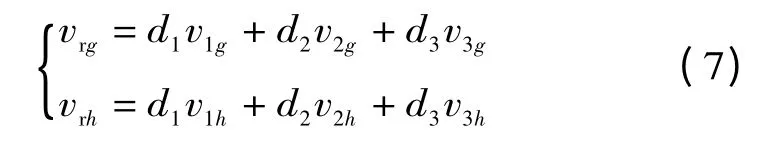
式中:d1+d2+d3=1。d1，d2，d3分别为各矢量的占空比。

2 不平衡电网电压下PR 控制器的设计

2.1 PR 控制器

PR 控制器是在αβ 静止坐标系下实现正弦量无静差控制，所以不需要进行多次坐标变换和前馈解耦，响应速度快，该控制器对系统模型依赖小，不需要非常精密的系统，鲁棒性好［14～16］。同时还具有非线性负载适应能力强，输出电压谐波总畸变率小，输出稳压精度高等特点。目前在滤波器和换流器中得到了广泛的应用和研究，其传递函数为

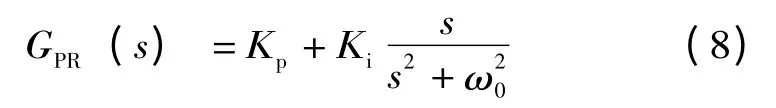
式中:Kp，Ki分别为比例常数、积分时间常数;ω0为谐振频率。

该PR 控制器在频率ω0处增益为无穷大，在非谐振频率处增益为0，在电压控制回路的频带宽度内，将几个PR 控制器并联使用可以减少输出电压的低次谐波含量。在实现对正弦量的无静差控制时，由于PR 控制器在谐振频率处的增益无穷大，电网电压微小的频率变化都将产生很大的偏差。为了解决这个问题，引入一种改进的准PR 控制器，其传递函数为［17］

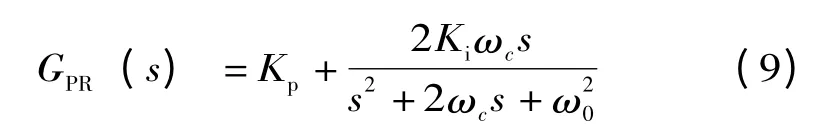
式中:ωc为截止频率，由图4 可知，随着截止频率ωc的增加，准PR 控制器即使在电网电压频率出现微小的偏差时也能够对其提供足够大的幅值增益。减小了对电网电压的灵敏度，但也增加了无静差控制的误差。需要选择合适的截止频率ωc进行折中。

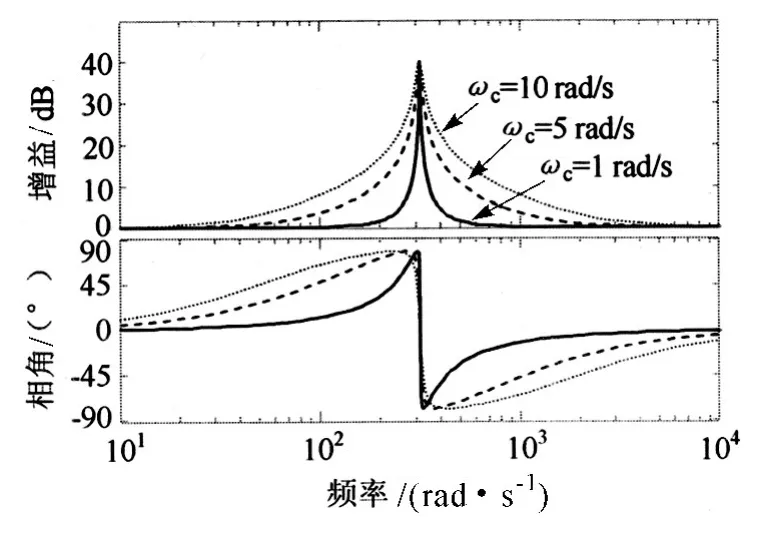
图4 PR 控制器的波特图

为了让准PR 控制器在数字信号处理器DSP中实现。对式(9)进行反拉普拉斯变换得到时域系统下的描述为

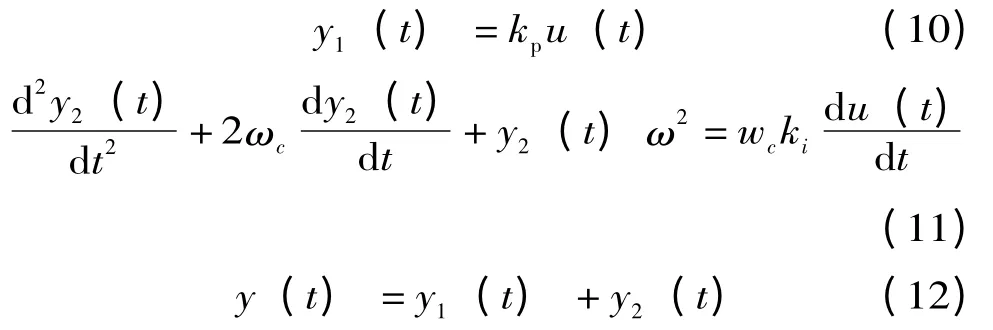
式中:y(t)为控制器的输出;y1(t)，y2(t)分别为式(9)的第一部分和第二部分的时域描述;u(t)为误差输入信号。

2.2 不平衡电网电压下控制问题分析

PI 控制是将αβ 静止坐标系中的正弦量转化为了dq 同步旋转坐标系中的直流量，从而使得可以利用PI 控制器完成对直流量的无静态误差的控制，PR 控制器传递函数的j 轴上加入两个固定频率的闭环极点，形成该频率下的谐振，从而增大该频率点的增益(理论上，谐振使得该设计频率下的增益趋近于无穷大)，实现对该频率下αβ 静止坐标系中的正弦量的无差跟踪。

在三电平TSMC 系统中，不平衡电压矢量由正、负序分量组成，电网电压矢量在αβ 静止坐标系下可以表示为

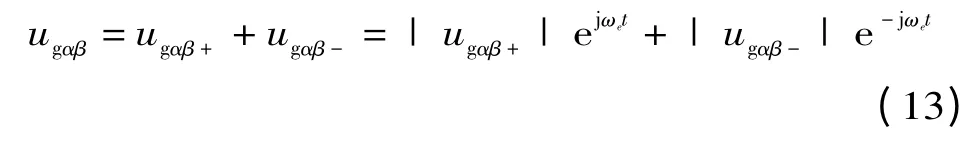
式中:下标g表示电网;α，β 分别表示静止α，β轴;+、-分别表示正、负序分量。

由式(13)可知，电网电压正、负在αβ 静止坐标系下都体现为交流量，当电网电压出现不平衡时，αβ 静止坐标中的电压为交流分量，传统的PI 控制器无法实现对交流信号的无静差控制，需要采用能够在αβ 静止坐标系无静差跟踪交流信号的PR 控制器。

2.3 逆变级PR 控制系统的构成

控制系统框图如图5 所示，为了在不平衡输出条件下，保证输出电压平衡稳定。本文中逆变级的PR 控制器以电压为控制对象，用电压闭环PR 控制代替传统的PI 控制，在αβ 坐标系下实现对给定输出电压的无静差跟踪。给定三相电压大小与检测到的三相电压在αβ 坐标系下做差值，然后经过PR 控制器得到αβ 坐标系下的电压参考信号。系统结构简单易实现，在逆变级SVPWM 调制中，以电压为闭环，可以通过改变给定电压大小和频率来实现输出电压幅值和频率连续可调。

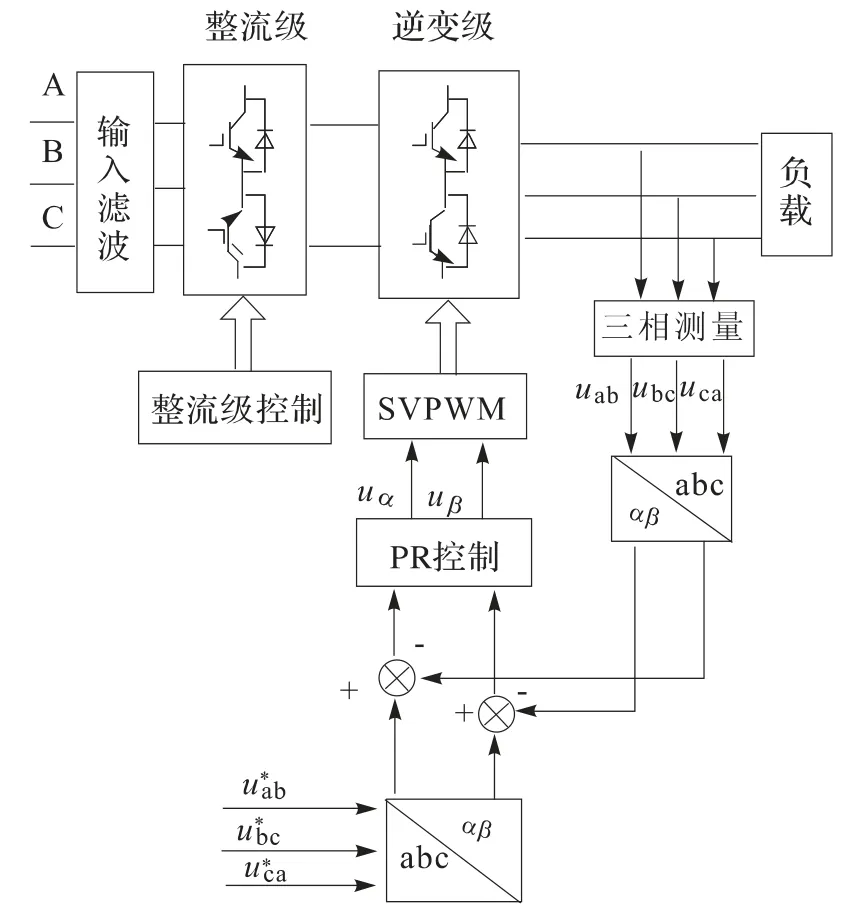
图5 逆变级PR 控制系统

3 结果与分析

3.1 输入平衡条件下PR 控制性能分析

主要参数:三相输入线电压380 V/50 Hz，输入滤波器参数R=56 Ω，L=0．5 mH，C=30 μF，感性负载功率为3 750 W，期望输出线电压380 V/150 Hz。

如图6 为输出参考电压为380 V/150 Hz 的仿真结果。由于三电平TSMC 中间直流环节无电容和钳位电路，所以中间直流电压为脉动波，如图6(b)所示。图6(c)为三电平TSMC 逆变级输出线电压Uab。

由图6(d)和图7 可以看出，采用PR 控制器的TSMC 输出电流质量良好，有效地抑制了低次谐波。图8 给出了在PI 控制下和PR 控制下输出不同频率时的电流畸变率对比图，可以看出PR控制器效果优于PI 控制器，输出谐波畸变率有较大改善。以输出150 Hz 为例，谐波畸变率从1．63%降低到0．67%，谐波减少59%。

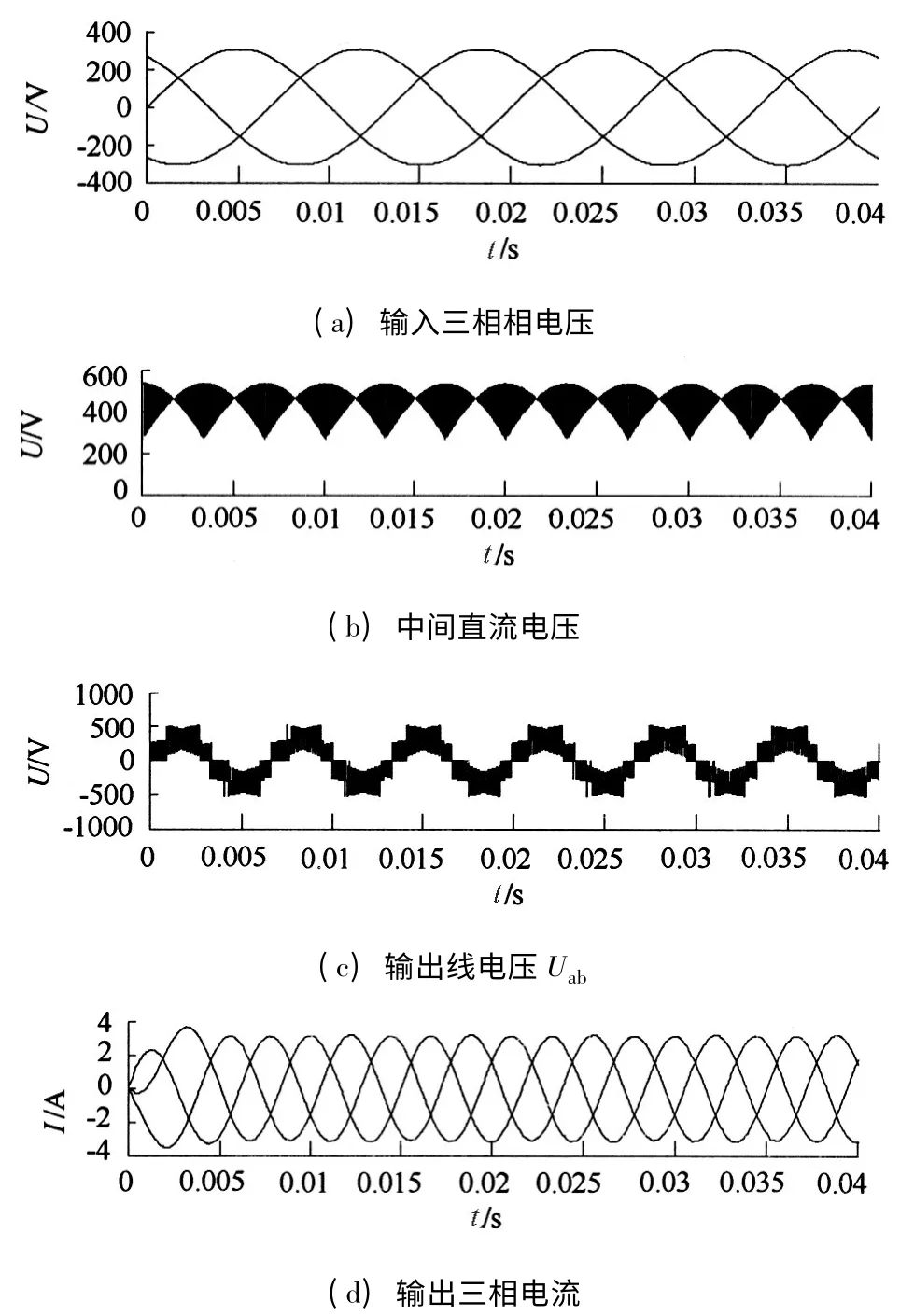
图6 输入平衡时采用PR 控制的仿真波形

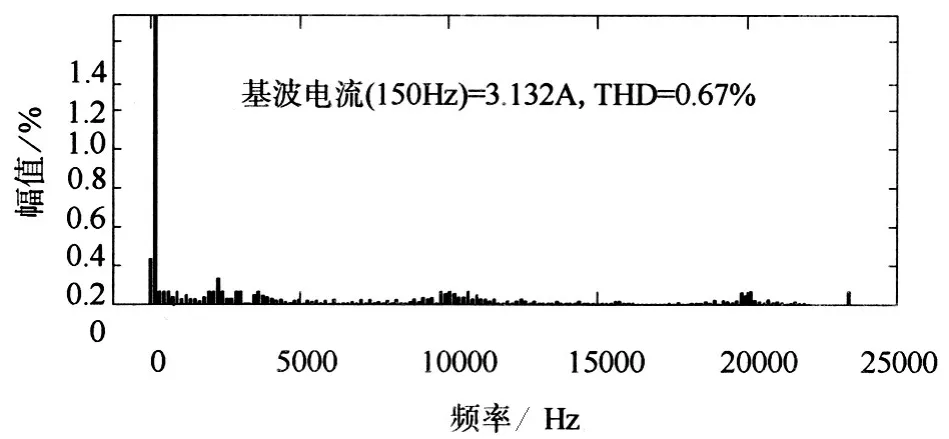
图7 输出电流畸变率

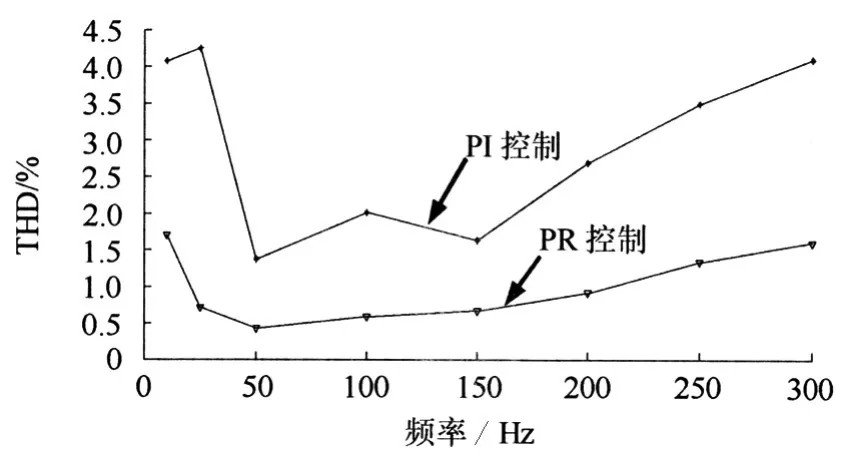
图8 平衡输入条件下输出电流畸变率对比

3.2 输入不平衡条件下PR 控制器性能分析

输入不平衡条件下，输入三相线电压幅值分别为350 V，380 V，300 V，电压不平衡度23．3%，如图9(a)所示。其他参数与输入平衡情况下相同，期望输出线电压380 V/150 Hz。

对比图9(b)和图6(b)可以看到当输入三相电压不平衡时，直接影响中间直流电压的脉动。图9(d)为PR 控制下输出电流，其峰值分别为3．152 A，3．145 A，3．154 A。图10 为PI 控制下输出电流，其峰值分别为3．571 A，3．96 A，3．868 A。可以看出PI 控制下的三相输出电流幅值相差较大，而PR 控制下的三相输出电流幅值误差很小，可以忽略，PR 控制器有效抑制了输入电压不平衡的影响。图11 为PR 控制下输入参考电压Uref跟踪实际输出平均电压Uavg。

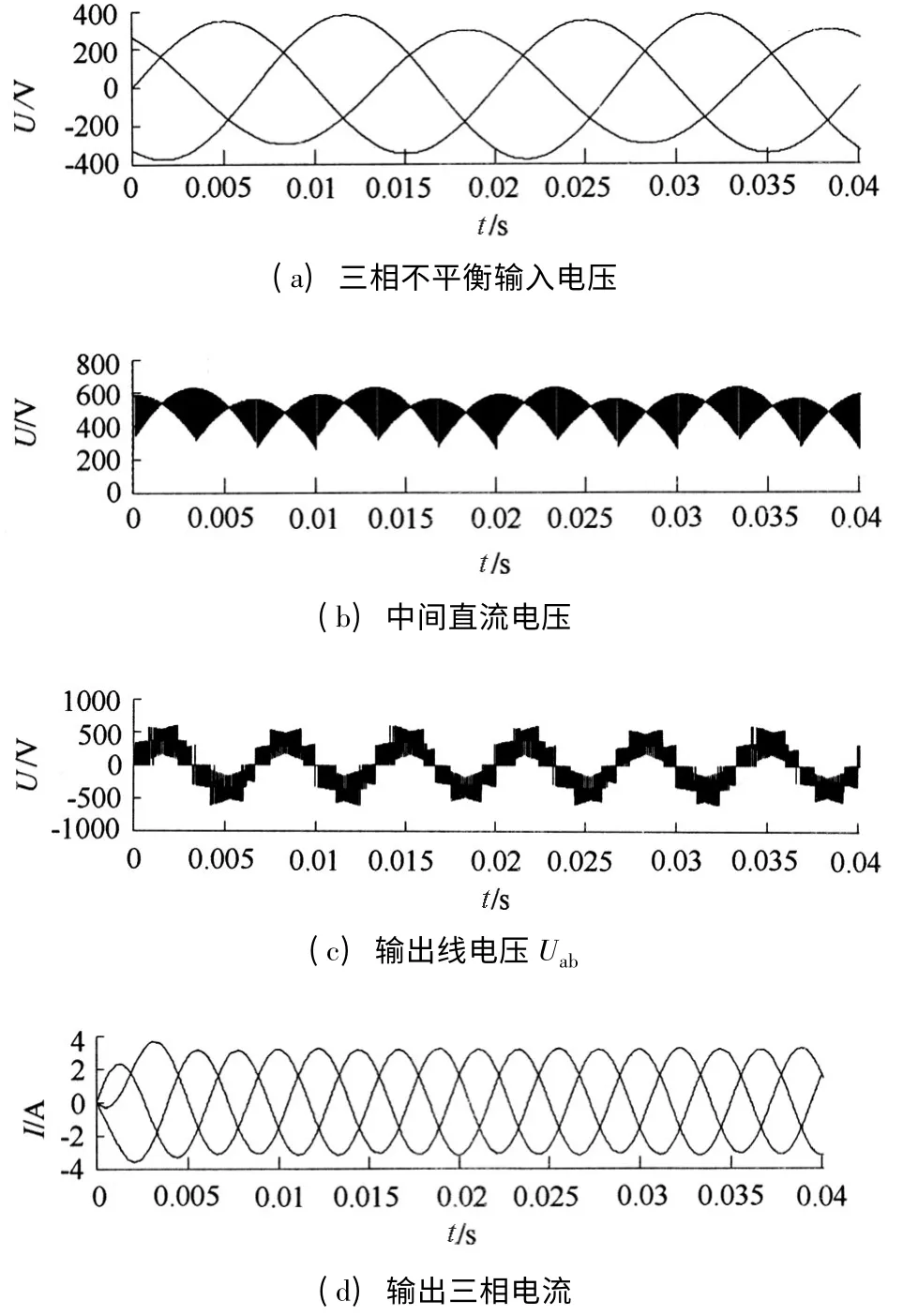
图9 输入不平衡时采用PR 控制的仿真波形

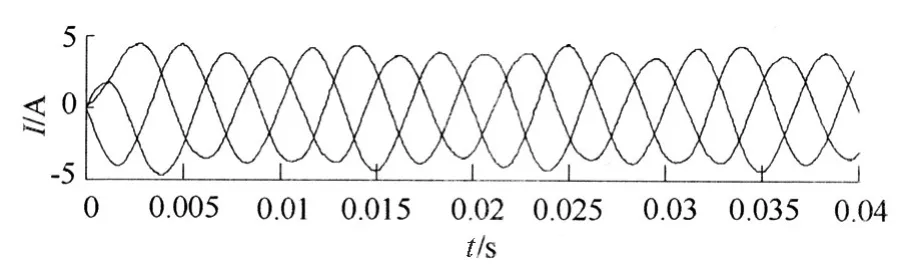
图10 输入不平衡时采用PI 控制的输出电流

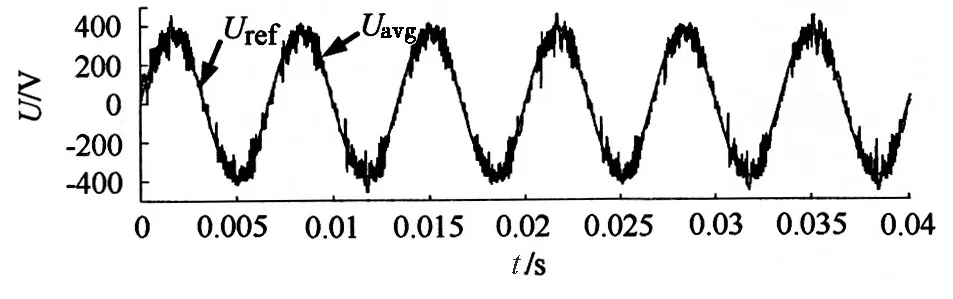
图11 PR 控制的输出参考电压与实际输出平均电压

4 结论

本文以三电平双级矩阵变换器为研究对象，针对输入电压不平衡问题进行研究，采用电压闭环PR 控制实现对输出电压的无静差控制，并将60°坐标系SVPWM 运用于三电平双级矩阵变换器，简化了计算。

仿真结果表明，采用电压闭环的PR 控制方式能够有效地抑制输入电压不平衡对输出的影响。输出电压频率、幅值皆连续可调，并且控制算法简单，易于数字化实现。该算法有效减少了输出波形的谐波含量，为三电平双级矩阵变换器在风力发电、变频调速等应用领域的推广应用提供了参考。

［1］邱麟，许烈，李永东．悬浮电容钳位多电平矩阵变换器拓扑与控制［J］．电力系统自动化，2014，38(8):79-83．

［2］王汝田，王秀云，崔永恒．矩阵变换器的谐波注入PWM 控制策略［J］．电力自动化设备，2013，33(8):77-82．

［3］王汝田，严干贵．矩阵变换器改进的双电压控制策略［J］．电力自动化设备，2012，32(2):39-43．

［4］Rodriguez J，Rivera M，Kolar W，et al．A review of control and modulation methods for matrix converters［J］．IEEE Transaction on Industrial Electronics，2012，59(1):58-70．

［5］齐琛，陈希有．一种简化换流的双级矩阵变换器混沌载波频率调制技术［J］．电工技术学报，2013，28(8):149-156．

［6］王兴伟，林桦，邓建，等．实际应用中的矩阵变换器空间矢量调制算法及优化调制模式［J］．中国电机工程学报，2011，31(30):7-15．

［7］Lee M Y，Wheeler P，Klumpner C．Space vector modulated multilevel matrix converter［J］．IEEE Transaction on Industrial Electronics，2010，57(10):3385-3394．

［8］Wang J C，Wu Bin，Xu D W，et al．Phase-shifting-transformer-fed multimodular matrix converter operated by a new modulation strategy［J］．IEEE Transaction on Industrial E-lectronics，2013，60(10):4329-4338．

［9］Song Weizhang，Zhong Yaneu，Ye Ying，et al．Study on modulation strategy with neutral-point balancing control for three-level two stage matrix converter［C］．International Conference on Materials Science and Information Technology(MSIT 2011)．Switzerland:Trans Tech Publications Ltd，2012．433-440．

［10］宋卫章，钟彦儒，孙向东．具有高电压传输比且能抵御非正常输入的Z–源双级矩阵变换器［J］．中国电机工程学报，2010，30(24):21-28．

［11］杨俊华，冯小峰，吴捷，等．基于广义预测的矩阵变换器电流环闭环控制［J］．电力自动化设备，2010，30(9):28-43．

［12］王永，关淼，张磊．一种三相四桥臂拓扑结构的新型矩阵变换器［J］．物理学报，2010，59(2):867-876．

［13］赵辉，李瑞，王红君，等．60°坐标系下三电平逆变器SVPWM 方法的研究［J］．中国电机工程学报，2008，28(24):39-45．

［14］Hamed N，Ahmad R．Current control assisted and non-ideal proportional resonant voltage controller for four-leg three phase inverters with time-variant loads［C］．4th Annual Internatiional Power Electronics，Drive Systems and Technologies Conference(PEDSTC)，Tehran，Iran:IEEE:355-360．

［15］孙玉坤，孙海洋，张亮．中点箝位式三电平光伏并网逆变器的三单相Quasi-PR 控制策略［J］．电网技术，2013，37(9):2433-2439．

［16］吴振兴，邹旭东，黄清军，等．应用低次谐波无静差消除策略的三相并联型APF［J］．电力系统自动化，2010，34(12):67-71．

［17］陈燕东，罗安，谢三军，等．一种无延时的单相光伏并网功率控制方法［J］．中国电机工程学报，2012，32(25):118-125．