基于超像素的多模态MRI脑胶质瘤分割
苏坡, 杨建华, 薛忠
(1.西北工业大学 自动化学院, 陕西 西安 710129; 2.Houston Methodist研究所, 美国 休斯顿 77030)
脑胶质瘤(glioblastoma multiforme, GBM)是脑肿瘤中最常见的、死亡率最高的一种恶性肿瘤。统计表明,40%的脑肿瘤患者为脑胶质瘤。脑胶质瘤患者术后存活时间的中位数仅为8个月,而5年以上的存活率几乎为零[1]。GBM在多模态MRI图像中呈现出一片异质的肿瘤区域。这片区域通常包括3个部分:坏死肿瘤(necrosis)、活动肿瘤(enhanced tumor)以及肿瘤挤压周围正常脑组织所形成的水肿(edema)。由于GBM肿瘤在组织形态上的复杂性与特殊性,单模态MRI无法清晰地反映GBM的不同组织结构。相比之下,多模态MRI图像中含有丰富的组织结构信息,被广泛用于GBM的诊断和治疗。本文的多模态MRI主要包括T2(T2加权成像)、T1PRE(T1加权成像)、T1POST(T1增强成像)和FLAIR (液体衰减反转成像)。在不同的模态下,GBM组织图像呈现出不同的特征:活动肿瘤在T1POST呈现高信号,坏死部分在T1POST呈现低信号,而水肿部分在T2和FLAIR呈现高信号。GBM的分割是指根据这些特征,把GBM组织从正常的脑组织中标记或分割出来。
文献中,基于像素或者体素的分割算法广泛应用于GBM的分割。这类算法的基本思想是根据每个像素在多模态图像上亮度信息、纹理信息等把该像素点分类到相应的类别中。分类的算法包括无监督的聚类和有监督的学习。例如,Clark等[2]提出了一种基于FCM(fuzzy C-means algorithm)的模糊均值聚类的算法。该算法以多模态图像的灰度作为特征向量,首先利用FCM对所有体素点进行聚类得到初始的分类,然后根据对称性,灰度分布等先验知识对初始分类进行优化,得到最终的分割结果。由于FCM聚类时,没有考虑空间邻域信息,并且GBM组织的灰度分布会产生重叠,因此容易产生误分割。
基于图形分割的算法[3-4]现在也非常流行。这类算法用图的顶点来描述图像的像素,用图的边描述2个像素的相似性,由此形成一个网络图,然后通过解决能量最小化问题把图分割成子网络图,使不同子网络图之间的差异和同一子网络图内部的相似性达到最大。这类算法通常需要解决一个求解广义特征向量问题,当图像比较大时,这类算法会遭遇计算复杂度大的问题。除了以上2类算法,基于Level set[5]的分割算法也广泛应用于GBM分割,但是由于GBM组织灰度不均匀,并且GBM组织之间经常没有明显的边界,采用这类算法容易出现边缘泄露的问题。
最近,超像素或超体素(supervoxel)[6-7]引起了很大的关注,基于超像素和超体素的分割算法也成为研究热点。相比于传统的像素和体素,超像素和超体素具有计算效率高,符合人类视觉感知,能高效表示图像信息等优点。
为了充分利用超像素的优点,提高GBM分割的精确性和鲁棒性,本文提出了基于超像素的多模态MRI GBM分割算法。首先通过带加权距离的局部k-均值聚类算法,把多模态MRI图像过分割成一系列均匀、紧凑并能很好地贴合图像边缘的超像素。然后,利用动态区域合并算法对超像素进行逐步合并。最后通过后处理得到GBM的最终分割结果。实验表明本文算法能取得较好的分割效果。
1 研究方法
1.1 算法框架
图1给出本文的算法框架。算法包含4步:①图像预处理,包括多模态图像的共同配准和去脑壳;②利用本文提出的带加权距离的局部k-均值聚类算法把多模态图像分割为一系列亮度均匀并能很好地贴合图像边缘的超像素;③利用动态区域合并算法对②产生的超像素进行合并。通过区域合并生成若干块均匀的有意义的区域(合并后的不同区域用不同的颜色表示,见图1);④根据亮度分布等对合并后的区域进行后处理,最终完成对GBM的分割。
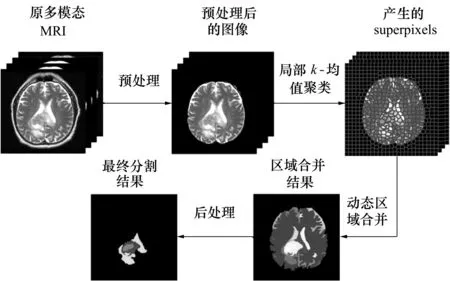
图1 算法框架
1.2 预处理
预处理包括多模态图像的共同配准(co-registration)和去脑壳。图像的共同配准保证多模态图像同一位置的像素对应脑部同一组织。本文利用FSL[8]的FLIRT工具完成对多模态MRI图像的共同配准。选取T2作为参考图像,把其他模态的图像配准到T2上。配准采用刚性变换并以互信息量作为图像相似性测度。
去脑壳是脑图像处理的一个常见步骤。它一方面可以减少后续处理的计算量,另一方面也会减少非脑实质组织对后续处理的影响。本文利用一个模板图像和它去脑壳后的图像,通过配准的方法实现去脑壳操作。首先把该模板脑图像通过仿射变换配准到T2上。接着用第一步配准产生的仿射变换矩阵对去脑壳后的模板图像进行变换就实现了对T2的去脑壳操作。
1.3 基于局部k-均值聚类的超像素生成
在文献[6]中,Achanta等提出了一种基于局部k-均值聚类算法,把彩色图像过分割为一系列均匀、紧凑并能很好贴合图像边缘的超像素。该算法的基本思想是根据像素点的图像特征和空间位置特征定义一个新的距离函数,然后根据新距离函数对像素点进行局部的k-均值聚类从而产生超像素。该算法主要输入参数为K,即待生成的超像素的个数。首先,在待分割的彩色图像均匀分布K个初始聚类中心点。根据K和整个图像像素点总数目N可以计算出初始聚类中心点之间的间距S:
(1)
然后,选取像素在CIELAB颜色空间的颜色值[lab]T和自身空间位置[xy]T组成5维特征向量[labxy]T。与传统的k-均值聚类采用欧式距离作为相似性测度不同,Achanta定义了一个新的相似性测度,该相似性测度考虑了所产生超像素的大小。新的相似性测度定义像素点i到第k个聚类中心的距离为
(2)
式中
(3)
(4)
(liaibixiyi)T表示第i个像素的特征向量,i∈[1,N]。(lkakbkxkyk)T表示第k个聚类中心的特征向量,k∈[1,K]。df为像素点i到第k个聚类中心的图像特征距离,测量2个像素亮度特征的相似性。dxy为像素i到第k个聚类中心的空间距离,测量2个像素空间位置的相似性。S为公式(1)中初始聚类中心的之间的空间间隔,它的引入相当于引入了超像素大小的信息。参数m控制所产生超像素的紧凑程度。m越大,空间距离dxy占主导,所产生的超像素就越紧凑;反之,m越小,亮度特征距离df占据主导,产生的超像素能更好地贴合图像边缘,但其大小和形状不是很紧凑。传统的k-均值聚类搜索范围为整个图像空间,为了减少k-均值聚类的计算复杂度,Achanta限定搜索范围为聚类中心周围2S×2S区域。这就是该算法被称为局部k-均值聚类的原因。
本文对Achanta的算法进行了扩展,实现从多模态MRI产生超像素。选取像素在T2、T1PRE、FLAIR和T1POST的亮度值[f1f2f3f4]T和空间位置[xy]T组成6维特征向量[f1f2f3f4xy]T。为了产生更好的超像素,我们对Achanta算法进行改进,提出了一种带加权距离的局部k-均值聚类。我们的依据是不同模态的图像对GBM分割的贡献不同,如T2和FLAIR含有比较多的水肿信息,T1POST含有较多的GBM坏死部分和活动部分信息。对T1POST模态进行强调,定义新的图像特征距离df:
(5)
参数ω(0<ω<1)为T1POST模态的权重,ω=0.25时各个模态图像的权重相等(标准局部k-均值聚类),ω>0.25时T1POST模态占图像特征距离的比重大于其他模态。ω的引入可以实现对超像素进行细调,使超像素在保持紧凑性的同时还能更好地贴合GBM活动肿瘤和坏死部分的边缘。空间距离dxy的选取跟Achanta的算法一致。
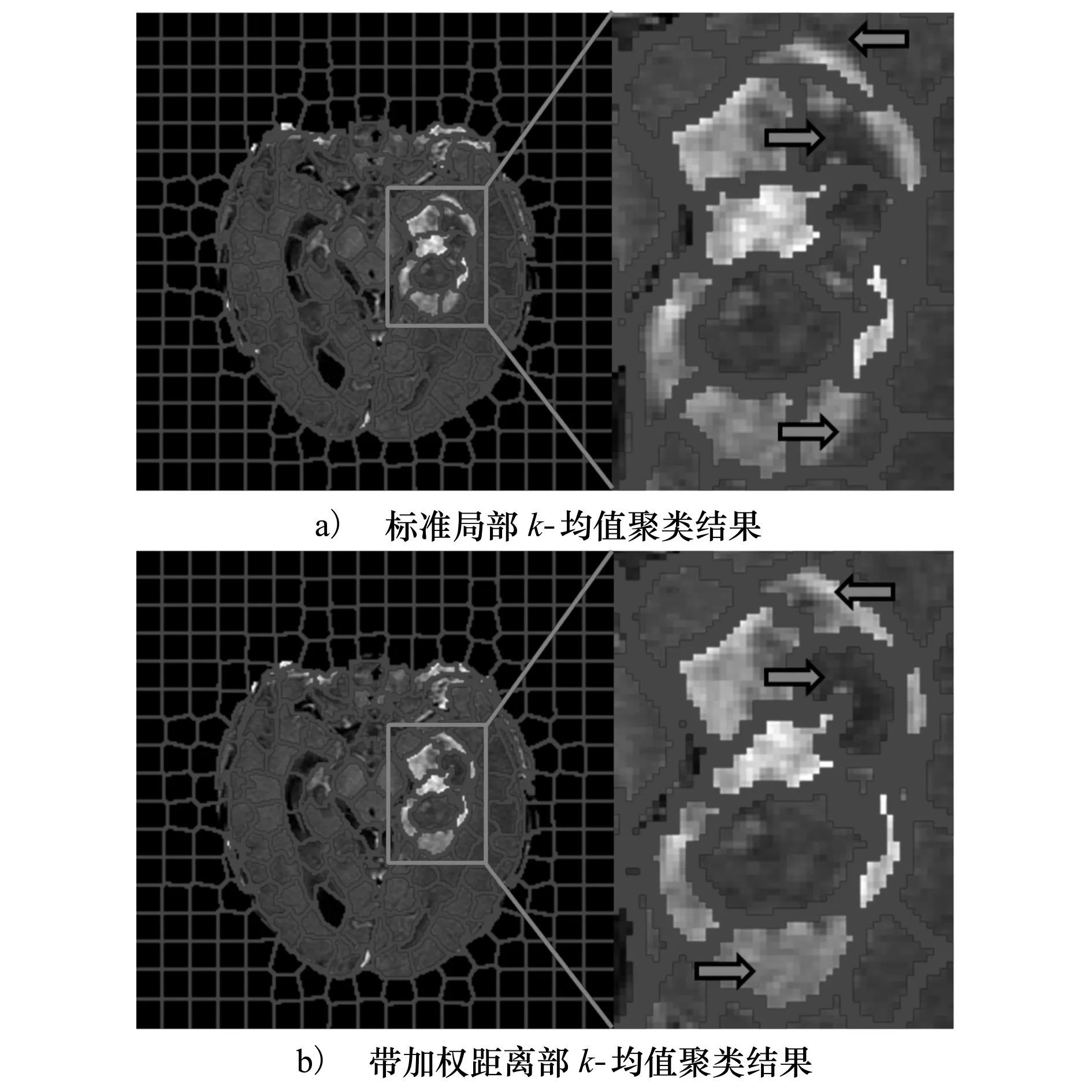
图2 采用标准局部k-均值聚类和带加权距离的局部k-均值聚类产生超像素的对比图
图2给出采用标准局部k-均值聚类(等权重距离)和加权距离k-均值聚类产生超像素的例子。其中设置K=300,m=70。从图2的箭头所指的超像素可以看出采用带加权距离k-均值聚类算法产生的超像素能更好地贴合GBM坏死部分和活动肿瘤部分的边缘。
1.4 动态区域合并算法
上一节中,多模态图像被过分割成一系列均匀、紧凑并能很好贴合图像边缘的超像素。如图3所示,多模态MRI被过分割成一系列超像素,参数设置K=600,m=70,ω=0.4。图3第一排图像依次为T2、T1PRE、FLAIR和T1POST模态图像;第二排和第三排显示用本文算法产生的超像素。

图3 多模态MRI图像被过分割成超像素
我们采用区域合并的方法对超像素进行处理进而实现对GBM的分割。为了方便起见,用区域邻接图(region adjacency graph, RAG)模型描述所产生的超像素。令G(V,E)表示一个无向图,vi∈V(i=1,2,…,M)为图的一个顶点,代表第i个超像素。E⊂V×V表示相邻的2个顶点的边,边的权重w(vi,vj)表示相邻的2个超像素i和j之间的相似度。
区域合并的过程就是根据区域邻接图顶点的相似性对顶点进行合并同时对相应的数据进行更新的过程。区域合并算法成功的关键在于能否解决2个问题:①设计区域合并的规则,即2个区域满足什么样的条件就对其合并;②设计合并停止条件,即区域合并到什么程度就停止区域合并。针对这2个问题,研究者提出了不同的区域合并算法。Nock等[10]采用相似性统计检验方法实现区域合并:若2个相邻的区域具有统计意义上的相似性,则对这2个区域进行合并,反之不进行合并。然而现有的大部分区域合并算法均存在容易产生过合并,欠合并或者两者混合的情况。针对现有区域合并算法的不足,Peng等[10]提出了一种动态区域合并算法并证明了该算法产生的区域合并结果能保持一定的全局属性。该算法把区域合并看做是一个由相似性度量和一致性度量2个部分组成的推断问题。相似性度量解决寻找候选合并区域的问题,一致性度量则决定是否对这些候选区域进行合并。在一致性度量部分,Peng引入序贯概率比检验(sequential probability ratio test, SPRT)方法,通过SPRT来确定候选区域是否具备一致性。实验结果表明Peng的算法优于其他区域合并算法。本文采用Peng的动态区域合并算法来实现区域合并。定义区域合并谓词P为:
P(v1,v2)=
v1和v2表示RAG中2个相邻的超像素v1和v2。w(vi,vj)为RAG 2个顶点vi和vj的相似度。Ω1和Ω2分别表示与v1和v2相邻的超像素的集合。谓词P(v1,v2)表示当且仅当同时满足条件(a):v1和v2互为最相似的邻居;条件(b):v1和v2具有一致性时对v1和v2进行合并,否则不进行合并。条件(b)暗含停止区域合并的条件。若没有条件(b),所有的超像素最终将合并成为一个区域。定义2个超像素vi和vj相似度w(vi,vj)为:
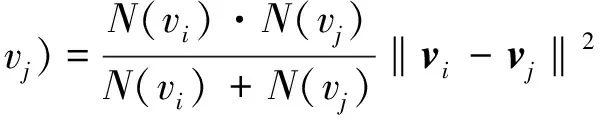
(6)
N(vi)和N(vj)分别表示超像素vi和vj中所含像素的个数。vi和vj均为向量,分别表示超像素vi和vj在4种模态图像的亮度平均值向量。
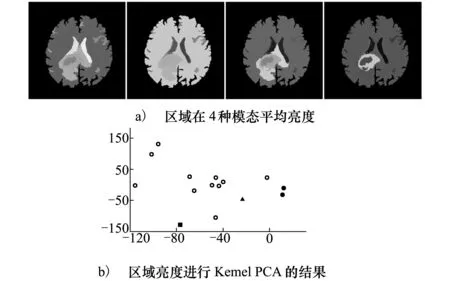
对于条件(b),Peng采用序贯概率比检验(SPRT)的方法来进行判断。定义零假设H0∶θ=θ0,即2个相邻的超像素vi和vj具有一致性;备择假设H1∶θ=θ1,即vi和vj不具有一致性。根据假设检验第一类错误的概率α和第二类错误的概率β确定2个阈值A和B(B<0 (7) 推断问题定义的断言是隐状态,不能直接观测,但它在统计上与可以直接观测到的信息x相关,这里x为多维随机变量代表超像素中的像素在各个模态图像的亮度。定义序贯似然比和序贯似然比累加和分别为: (8) 式中:P0(xi|θ0)和P1(xi|θ1)为第i次抽样观测到x的条件概率,这里用高斯分布模型来近似x的分布,这2个条件概率可以表示成: (9) Ia和Ib均为向量,分别表示对待合并的相邻超像素vi和vj进行随机抽样(抽样个数为各自所含像素数目的一半)后,各自样本4种模态亮度的均值;Ia+b为这2个超像素所组成的大区域中所有像素4种模态亮度的均值;CI表示这2个超像素所组成的大区域所有像素4种模态亮度的协方差矩阵;λ1和λ2为2个标量参数。 为了解决SPRT检验中抽样检验次数的不确定性问题,采用截断型SPRT检验算法,即预设一个最坏情况抽样次数的上限N。然后根据下面的规则对假设的2种模式进行判断: 其中n表示第n次抽样。本文所有实验SPRT参数均设为α=0.05,β=0.05,N0=10,λ1=10,λ2=1。 根据区域合并的条件(a)和条件(b)反复地对相邻的超像素进行合并和更新直至所有两两相邻的超像素不能合并为止,就完成了整个区域合并过程。 通过动态区域合并,超像素最终被合并为大大小小的几十个区域。由于区域合并是对相邻的区域进行合并,而实际情况是GBM同一组织空间上可能是不相邻的,因此需要对合并结果进行后处理进而得到最终的GBM分割。 首先根据亮度和空间位置剔除掉与背景相邻的大脑外围的脊髓液区域和去脑壳没有去除干净的非脑实质组织区域。脊髓液在FLAIR模态为低亮度,而未被去除干净的非脑实质组织的区域所含的像素数目比较少。因此可以事先设定FLAIR亮度阈值和像素数目阈值剔除以上组织。接着用区域中所有像素在4种模态的平均亮度作为区域的4种模态亮度,见图4a)。我们对区域的4种模态亮度进行Kernel PCA[13]降维,把四维降至二维。图4b)为对区域4种模态亮度进行Kernel PCA降维后的结果,其中实心圆点代表水肿区域,实心方块代表活动肿瘤部分,实心三角代表坏死部分。然后对区域亮度Kernel PCA降维后的结果进行k-均值聚类,再根据不同组织在不同模态图像亮度的分布规律就可以得到最终的分割结果见图5。k-均值聚类时,我们可以从Kernel PCA的结果观察得到k-均值聚类的类别数k,例如在根据图4b)设定聚类数目k=7、8。注意在聚类的过程中,同时加入如下约束:若k-均值聚类时2个相邻的区域被分为一类,则不把这2个区域划为一类,因为动态区域合并的结果表明它们不具有一致性。如图4b)所示,距离2个实心圆点最近的那个空心点,按照标准k-均值聚类,这个空心点极有可能跟这2个实心圆点归为一类,但是由于它和其中的一个实心圆点在实际空间位置上相邻的,根据附加约束这个点不能和实心圆点归为一类。 图4 区域合并后的区域亮度进行Kernel PCA结果 图5 最终分割结果(灰度值从高到低依次为水肿、坏死和活动肿瘤) 为了评价新算法的性能,本文对15个GBM病人的多模态MRI脑图像数据进行定性和定量实验。每个病人多模态MRI图像包括T2,T1PRE,FLAIR和T1POST,每种模态的图像大小均为256×256×21, 图像的分辨率为0.78 mm×0.78 mm×6.5 mm。本文算法的性能依赖于超像素的质量。超像素主要由K,m和ω控制。通过反复实验,我们设定K=600,m=70,ω=0.4。 为了定量评估新算法的性能,我们把本文算法和其他2种经典分割算法进行比较,这2种经典算法是:基于FCM算法[2]和Ncut[3]。 我们选用Dice相似性系数评价分割算法性能。Dice相似性系数的定义为: (10) A表示医生手动分割的GBM组织像素的集合,B表示分割算法分割出来的GBM组织像素的集合。Dice相似性系数越大,表明分割的结果越好。图6给出本文算法和基于FCM算法,Ncut算法的性能比较图。从图6可以看出和其他2种经典算法相比,本文的算法更加精确。 图6 算法性能比较图 本文提出了一种基于超像素的多模态MRI脑胶质瘤分割算法:把超像素和动态区域合并这2种算法结合到一起,充分利用2种算法各自优点,提高GBM分割的鲁棒性和准确性。对15个GBM病人数据的对比实验证明了本文算法的先进性。 参考文献: [1] Patel M R, Tse V. Diagnosis and Staging of Brain Tumors[J]. Seminars in Roentgenology, 2004, 39(3): 347-360 [2] Clark M C, Hall L O, Goldgof D B, et al. Automatic Tumor Segmentation Using Knowledge-Based Techniques[J]. IEEE Trans on Medical Imaging, 1998, 17(2): 187-201 [3] Shi J B, Malik J. Normalized Cuts and Image Segmentation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905 [4] Corso J J, Sharon E, Dube S, et al. Efficient Multilevel Brain Tumor Segmentation with Integrated Bayesian Model Classification[J]. IEEE Trans on Medical Imaging, 2008, 27(5): 629-640 [5] Ho S, Bullitt E, Guido G. Level-Set Evolution with Region Competition: Automatic 3-D Segmentation of Brain Tumors[C]∥IEEE International Conference on Pattern Recognition, 2002: 532-535 [6] Achanta R, Shaji A, Smith K, et al. SLIC Superpixel Compared to State-of-the-Art Superpixel Methods[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282 [7] Lucchi A, Smith K, Achanta R, et al. Supervoxel-Based Segmentation of Mitochondria in EM Image Stacks with Learned Shape Features[J]. IEEE Trans on Medical Imaging, 2012, 31(2), 474-486 [8] Smith S M, Jenkinson M, Woolrich M W, et al. Advances in Functional and Structural MR Image Analysis and Implementation as FSL[J]. Neuroimage, 2004, 23: 208-219 [9] Nock R, Nielsen F. Statistical Region Merging[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(11): 1452-1458 [10] Peng B, Zhang L, Zhang D. Automatic Image Segmentation by Dynamic Region Merging[J]. IEEE Trans on Medical Imaging, 2011, 20(12): 3592-3605 [11] Schölkopf B, Smola A, Müller K R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J]. Neural Computation, 1998,10(5):1299-1319
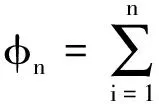
1.5 后处理

2 实验结果与分析

3 结 论

