基于改进2D-2DPCA的图像融合算法

夏余, 曲仕茹, 李珣

(西北工业大学 自动化学院, 陕西 西安 710129)

图像融合作为信息融合技术的一种已在智能交通以及军事等领域得到了广泛应用。采用图像融合的智能图像信息获取技术可有效处理图像理解和模式识别中的不确定性问题,实现多源图像信息的协同利用,生成多元信息互补,对同一目标或场景相对于单一传感器获取的信息具备更高级解释的图像内容。鉴于人类视觉中色彩信息的可辨识度远远高于灰度信息和机器视觉对图像信息量的要求,伴随着传感器技术的不断改进和提高,色彩图像融合在图像处理领域得到广泛关注。

目前较为经典的色彩融合方法有NRL法[1]、MIT法[2]、TNO法[3]和基于颜色传递技术的Toet方法[4]。然而,上述方法均为伪彩色图像融合方法,色彩融合的同时对纹理和细节等图像信息造成了较大的损害,且融合图像的颜色质量对融合选取的参考图像有很强的依赖性。

目标图像及源图像包含彩色信息的融合过程,不需要考虑参考图像的选取,只利用源图像的颜色分布便可完成。但是,常用的RGB色彩空间各分量之间存在着很大的相关性,不能独立地改变各通道的色彩表述。一些经典的基于空间变换的色彩图像融合算法,如PCA融合算法、IHS融合方法,基于彩色信息传递的图像融合方法[5]。PCA方法在去除各通道相关性的同时无法兼顾原有图像的结构信息,IHS方法能保留高分辨率信息但会引入较严重的色彩畸变[6],lαβ变换的计算过程是非线性的指数和对数变换不利于运算。且YCBCR、IHS和lαβ等空间变换的色彩图像融合算法采用固定的过渡矩阵对所有图像进行空间变换,这样将会大量保存RGB颜色空间各通道间的相关性。

为此,本文提出了一种改进的双向二维主元分析方法,并将其应用到色彩图像融合中。分别针对目标图像和源图像进行运算,以行、列方向的RGB分量作为基元进行二维主元分析得到各级主元,依照主元替代原则加以改进进行主元反变换,最终得到融合图像,去除RGB各通道的相关性的同时,保留高分辨率信息和红外热图像的能量信息,根据待融合图像的颜色和结构特性计算过渡矩阵,大大降低了色彩畸变,可以获得令人满意的融合效果。

1 算法描述

针对色彩空间变换时产生的色彩畸变和各RGB分量间的强相关性,本文采用基于改进双向二维主元分析(two directional two dimensional principal component analysis, 2D-2DPCA)的色彩图像融合算法,算法优势在于:

1) 运用二维主元分析的算法特性去除RGB各通道间的相关性;

2) 过渡矩阵根据RGB空间特性计算产生,降低了色彩空间变换产生的色彩畸变;

3) 采用行列结合的主元分析保存了原始图像的结构特性;

4) 采用本文的主元替换原则可保留热能量信息和彩色源图像的颜色信息,为融合结果的后续应用提供可靠的信息保证。算法流程如图1所示。

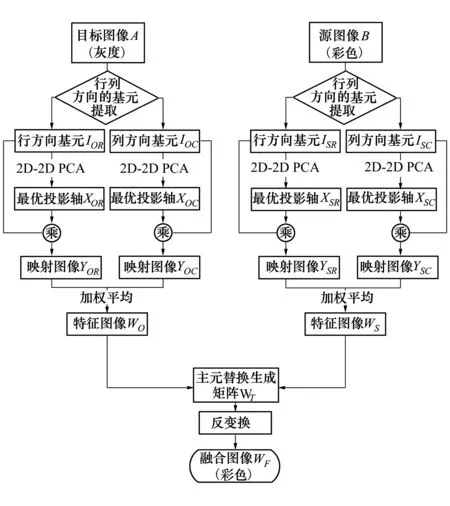
图1 双向二维主元分析色彩图像融合框架

由图1可以看出得到特征图像WO和WS的运算过程相同,我们以目标图像A的特征图像WO的运算过程为例进行算法描述。

1.1 基元选取

由上所述,在对图像进行融合之前需要选取适当的基元,有别于传统2D-2DPCA[7]以每幅图像作为基元的选取准则,本文分别以源图像及目标图像行和列方向上的RGB分量作为基元,当待运算图像为灰度时,算法认为RGB 3层数值与R层相同,基元提取方法如图2所示:

由图2可见,对于目标图像A来说,它是一个m×n的RGB图像,按行和列方向分别提取n个m×3和m个n×3的矩阵作为待处理的“图像”IOR和IOC,作为后续二维主元分析的输入。

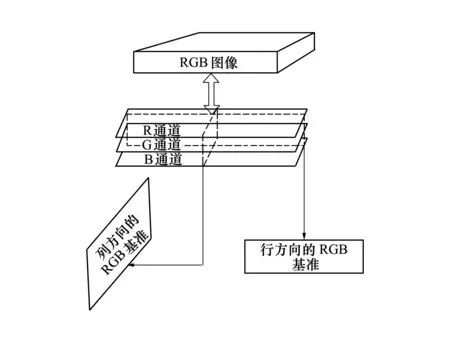
图2 基元选取示意图

1.2 改进的双向二维主元分析

1.2.1 二维主元分析

二维主元分析,二维主元分析算法(two dimension principal component analysis, 2DPCA)于2004年提出并用于人脸图像表示与识别[8]。它成功地将PCA算法提升到二维空间中加以运算。我们首先以上一节提取的行方向上的基元IOR为输入图像进行2DPCA运算。

设XOR表示一个三维列向量,2DPCA把大小为m×3的“图像”矩阵IOR,通过(1)式的线性变换投影到向量XOR上:

YOR=IORXOR

(1)

YOR为图像IOR的投影特征向量,最佳投影轴XOR可以根据特征向量YOR的散布情况来决定。由此可见,可以使用投影后向量的总离散度作为准则函数J(XOR)来衡量投影矩阵XOR的优劣,使总散度最大的XOR最优,记图像的协方差矩阵为:

GOR=E[(IOR-EIOR)T(IOR-EIOR)]

(2)

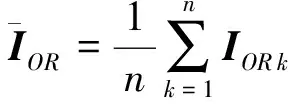
(3)

所以准则函数[13]可以写成

(4)

其中使准则函数J(XOR)最大的XOR的列向量为协方差矩阵G的最大的d个特征值对应的特征向量,即

XOR=(XOR1,…,XORd)=argmax[J(XOR)]

(5)

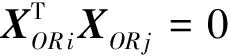
经过上述对目标图像A行方向上基元IOR的二维主元分析,使图像序列各颜色通道间的相关性得以降低,同时保持了图像序列行方向上的结构特性。同理我们可以得到列方向上的基元IOC对应的最优投影轴XOC。

1.2.2 特征图像的建立

经过行列2个方向的2DPCA运算我们得到最优投影矩阵XOR与XOC,将IOR和IOC映射到XOR与XOC求出映射图像YOR、YOC:

YOR=IORXORYOC=IOCXOC

(6)

它们由主元分量代替原有的RGB分量构成,主元分量由RGB分量按照主元级别由高到低的准则映射产生,且当d取3时为完全映射子图,显然XOR与XOC均为3×3的矩阵。YOR、YOC皆为原图像的完全映射图像,但两者分别为目标图像行和列方向的映射图像,且变换后的各层通道包含着各级主元信息,我们记λOR和λOC分别为协方差矩阵GOR和GOC的特征值,通过上述过程可知特征值λOR和λOC大小决定投影矩阵XOR与XOC的结构特征,进而影响映射图像。

针对映射图像YOR与YOC本文采用线性权重分配方法,来构造最终的重构图像。直观而言,协方差大的图像往往颜色信息丰富,纹理突出,应该获得较大权重,考虑到图像可能在行方向(或列方向)上信息显著,因此有必要针对图像自身的特点,选择使用行、列信息的使用权重：

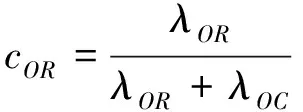
则目标图像A的特征图像WO为:

WO=cORYOR+cOCYOC

(7)

同样的,我们可以得到源图像B的特征图像WS。

2 2D-2DPCA逆变换

2.1 主元替换

按照上述运算准则我们得到了特征图像WO和WS,已去除各通道之间的相关性。为此我们可以根据实际需求以及图像的结构特征进行主元替换,出于对目标图像的高分辨率或热量信息和源图像饱满颜色信息的考虑,本文将WO的第一层矩阵WO1替换WS的第一层矩阵WS1,WS2及WS3作为重构矩阵WT的信息补充,即

WT=[WO1,WS2,WS3]T

(8)

由(8)式可以看出,重构图像WT结合了2幅图像的显著性特征,拥有高分辨率或热量信息和饱满颜色信息的结构特征。

2.2 逆变换

经主元替换后的重构矩阵WT是由目标图像A与源图像B的各级主元分量组成的,它不能直观呈现融合图像的颜色信息,因此需要对其进行逆变换回RGB颜色空间。由于源图像B行、列方向的最佳投影轴XSR和XSC为饱满颜色信息与主元分量的映射介质,所以以XSR和XSC为投影轴对重构矩阵进行逆变换。

设WT的行、列方向的主元分量分别为IWR和IWR,且可知XSR和XSC是正交矩阵,则行、列方向上的逆变换图像分别为:

(9)

其中YWR=IWRXSR,YWC=IWCXSC。

采用1.2.2小节的权重分配原则,记λSR和λSC分别为协方差矩阵GSR和GSC的特征值,GSR、GSC分别为源图像B经行、列方向的2DPCA运算获得。设最终产生的融合图像为WF,令

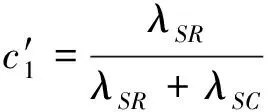
则最终的融合图像WF为:

(10)

3 实验结果及分析

3.1 实验结果

为验证本文方法的有效性，分别以一组校园NIR图像、公开发表的OCTEC数据库和OSU Color and Thermal Database作为实验素材进行色彩图像融合，图3至图5上方为目标图像与对照的源图像，下方是前文提到的PCA方法、加权融合方法、文献[5]方法和本文方法的效果对比。

图3 遥感图像色彩融合效果 图4 OSU(场景1)色彩图像融合效果 图5 OCTEC2(有烟雾干扰)色彩图像融合效果

3.2 实验分析

为衡量融合图像的整体质量,我们选用平均梯度、颜色丰富度和色彩图像熵作为客观评价标准对融合结果进行评价。平均梯度可敏感反映融合图像对微小细节反差的表达能力,被用来评价融合图像的清晰程度。空间梯度越大,说明图像层次越多,融合图像越清晰;彩色图像熵值越大,说明融合图像包含的信息量越大;颜色丰富度是表示颜色鲜艳程度的一个测量度,越大越鲜艳。由于彩色图像的像素值为三维向量,其梯度计算方式如下:

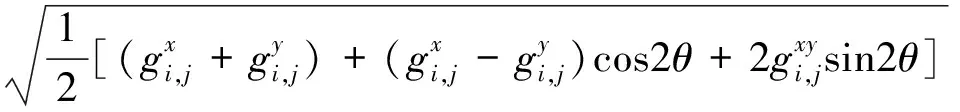
(11)

(12)

对融合图像的平均梯度计算结果见表1。

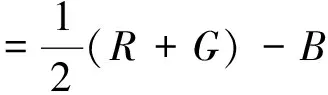
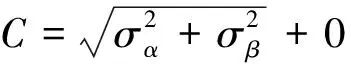
(13)

式中：σα、σβ与μα、μβ分别为α、β的标准方差和均值。融合图像的颜色丰富度计算结果见表2。

色彩图像熵定义为RGB 3个通道熵之和:

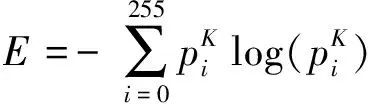
(14)

式中：pi为图像中灰度为i的概率。熵值越大,说明融合图像包含的信息量越大。对融合图像的色彩图像熵计算结果见表3。

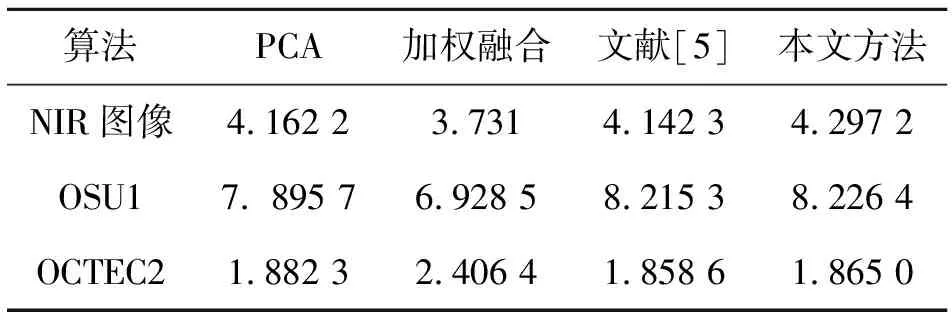
表1 融合图像的平均梯度

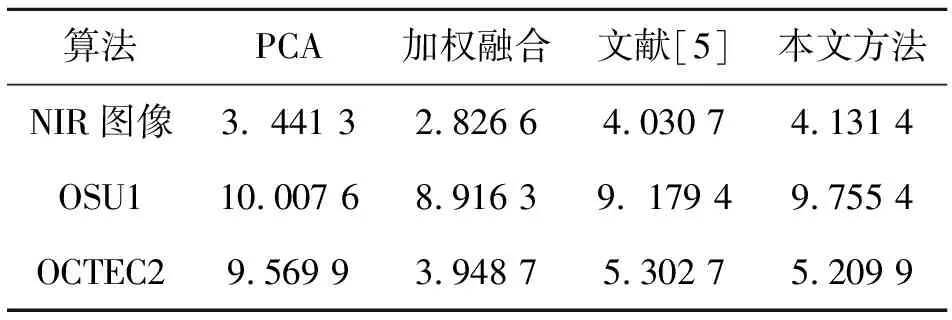
表2 融合图像颜色丰富度

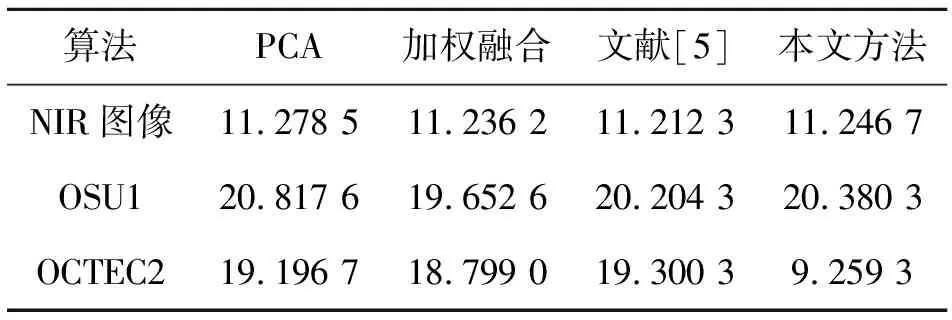
表3 融合图像色彩图像熵

图3为校园NIR图像色彩融合结果,可以看出,采用PCA方法的融合结果保证了图像的纹理信息和分辨率,但有明显的色彩偏差;加权融合方法的融合结果体现了其算法特性,包含了待融合图像的部分纹理信息和色彩信息,但同时直接对二者整体的数据结构直接加权,会导致融合图像的分辨率较低,且颜色信息损失较多;文献[5]方法和本文方法的融合结果较为理想,但文献[5]方法融合图像的局部亮度较本文方法低,清晰度和色彩图像熵略小于本文方法,视觉舒适度稍逊。

图4至图5为红外与彩色可见光图像的融合结果,图4、图5的前景目标均为行人目标,可以看到除加权融合方法对红外目标的呈现不够明显外,其余所有的融合结果都能突出红外目标的能量特性。但采用PCA方法的融合结果在背景颜色的呈现上依然存在色彩偏差,而这种偏差则体现在颜色丰富度的数值偏高上,这是由于此方法进行PCA运算时以单一像素点的RGB分量作为运算基元,没有考虑图像各通道的行列特性,在二维空间上,像素颜色值是以某种分布存在的,且某个特定像素的颜色值与它的某个邻域相关。文献[5]和本文方法则考虑到了这一因素,但文献[5]方法受红外图像中低灰度值像素位置的影响较大,导致融合结果背景区域较暗,使用本文方法生成的融合图像对红外目标的保留十分完整,并且背景颜色受红外图像影响相对较小。从各个彩色图像评价指标来看,文献[5]与本文方法相差不大,且本文方法略高。

综上所述,采用本文方法得到的融合图像在保留红外图像能量信息的同时丰富了色彩信息,对色彩和轮廓信息损失较多的红外图像和不包含热成像信息的可见光图像的融合结果可兼具两者的优势信息,从而能够增强融合图像的可辨识性,为后续工作提供可靠的信息支持。

4 结 论

提出了改进2D-2DPCA的色彩图像融合框架,以待处理图像行和列方向上的RGB分量作为基元,分别进行和列上的2DPCA运算,充分利用了双向二维主元分析对结构信息的保持特性和消除RGB各通道间相关性的特性,采用主元替换准则和基于协方差矩阵特征值的加权逆变换得到最终的融合图像。实验结果表明,对于包含色彩信息的图像融合本文算法有显著的优越性。

参考文献：

[1] Mcdaniel R, Scribner D, Krebs W. Image Fusion for Tactical Applications [J]. SPIE, 1998, 3436: 685-695

[2] Fay D A, Waxman A M, Ireland D B, et al. Fusion of Multisensor Imagery for Night Vision: Color Visualization, Target Learning and Search[C]∥3rd International Conference on Information Fusion, Paris, 2000

[3] Toet A. Color the Night: Applying Daytime Colors to Nighttime Imagery [C]∥Enhanced and Synthetic Vision 2003,Proceedings of the SPIE, 2003: 168-178

[4] Toet A. Natural Color Mapping for Multiband Nightvision Imagery [J]. Information Fusion, 2003, 4(3): 155-166

[5] Miranda-Hernndez J, Castela N M, Torres-Mendez L A. Face Colour Synthesis Using Partial Least Squares and the Luminance-/α/-β Colour Transform [J]. IET Computer Vision, 2012, 6(4): 263-272

[6] 敬忠良,肖刚,李振华.图像融合——理论与应用[M]. 北京:高等教育出版社,1999

Jing Z L, Xiao G, Li Z H. Image Fusion: Theory and Applications [M]. Beijing: Higher Education Press, 1999 (in Chinese)

[7] Zhang D Q, Zhou Z H. (2D)2PCA: Two-Directional Two-Dimensional PCA for Efficient Face Representation [J]. Neurocomputing, 2005, 69(1/2/3): 224-231

[8] Yang J, Zhang D, Alejandro F F, et al. Two-Dimensional PCA: A New Approach to Appearance-Based Face Representation and Recognition [J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137