基于红外传感器方位跟踪算法的性能分析

李伟, 羊彦, 侯静

(1.中航工业西安飞行自动控制研究所, 陕西 西安 710065; 2.西北工业大学 电子信息学院, 陕西 西安 710129)

对于战术导弹的MMW/IR双模导引头,当雷达出现故障或持续受到干扰时,只能利用红外观测数据进行目标跟踪。由于红外导引头只提供目标角度信息,就涉及到红外纯方位跟踪的问题。纯方位跟踪(bearings-only tracking, BOT)利用运动目标本身的有源辐射,采用机动单站测向机或观测站测得目标的方位信息序列实时估计目标运动参数(位置、航向、速度等)[1]。单站BOT是一个非线性问题,且根据目标运动分析(target motion analysis,TMA)的理论,当目标和导弹间的相对加速度为零时,目标的距离状态是不可观测的。因此,纯方位目标跟踪问题一直是研究的热点及难点问题[2]。目前纯方位TMA问题的常见解决方法为:几何定位法(四方位法)和滤波法。其中几何定位法研究最早,但由于纯方位TMA问题的非线性,不利于几何定位方法的使用。随着现代信号处理技术的发展,目前滤波法的研究主要集中在:滤波算法的研究和坐标系的选择[3]。

滤波算法方面,卡尔曼滤波(KF)的应用最广[4]。由于观测量是目标角度信息,在直角坐标系中,其测量方程是非线性的,KF无法直接使用。针对上述非线性问题,近年来无迹卡尔曼滤波(UKF)和粒子滤波(PF)等非线性滤波法得到了广泛关注,但其计算量巨大,不适于实时应用场合。目前工程上最常用的仍是扩展卡尔曼滤波(EKF),但EKF的BOT性能无法达到最佳,且可能存在滤波发散的问题。此外,伪线性卡尔曼滤波或称为伪线性估计(PLE),通过修改测量方程改善了滤波器的稳定性。但为保证PLE法的跟踪效果,要求观察者(即导弹)进行机动且机动轨迹为最佳(或接近最佳)[5];此外受测量噪声的影响,PLE算法是有偏的[6]。

坐标系方面,近年来讨论较多的是修正球坐标(Modified Spherical Coordinates,MSC)中的卡尔曼滤波法[7]。该算法稳定且渐近无偏,在修正的极坐标中建立数学模型,而滤波计算仍采用EKF。其状态变量包含目标角度、速度和距离信息,但滤波过程不够准确,存在很大误差。本文结合某型双模导引头的工程背景,针对纯方位TMA问题,设计了EKF、PLE和MSC中的EKF算法,并给出了可观测条件;通过对3种滤波方法的性能进行仿真比较,结合工程实际选择导弹被动跟踪时的最佳模型。

1 纯方位跟踪问题分析

红外纯方位目标跟踪系统无法获得弹目距离,因此系统的可观测性成为TMA中的一个困难问题。对纯方位TMA来说,当方位数据由单基站测量得到时,在导弹机动前,上述估计问题是不可观测的[8-9]。本文主要研究弹目相对运动时的跟踪问题,不涉及可观测性的讨论。

在三维直角坐标系下,假设目标以初速度vt(0),加速度at(t)做匀加速运动;导弹以初速度vm(0),加速度am(t)进行机动,其初始加速度为am(0)。则目标相对导弹的距离为r,速度为v(t)=vt(t)-vm(t),加速度为a(t)=at(t)-am(t)。暂不考虑噪声,定义系统的状态向量为X=[r,v,a]T,则系统的状态方程描述为:

(1)

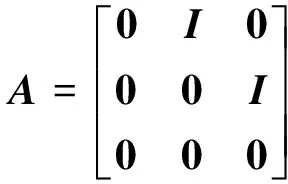
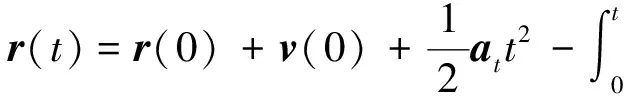
(2)

目标的纯角度观测φ(t)和θ(t)构成的系统观测方程为:

(3)

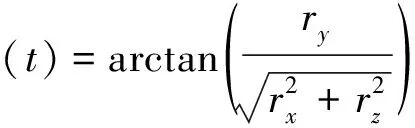
(4)

(1)式、(3)式和(4)式描述的系统面临的问题是:通过目标的纯角度观测φ(t)和θ(t)能否估计状态向量X,且估计精度如何。

2 纯方位目标跟踪算法

2.1 扩展卡尔曼滤波

纯方位目标跟踪的EKF算法是在常规KF的基础上,把非线性问题进行近似处理而得到的。红外目标跟踪的状态方程及观测方程为:

Xk=Φk,k-1Xk-1+GWk-1

(5)

Zk=HkXk+Vk

(6)

式中：Wk和Vk是相互独立的零均值高斯白噪声,其协方差阵分别为Q和R,

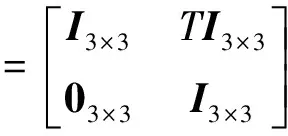
Hk=

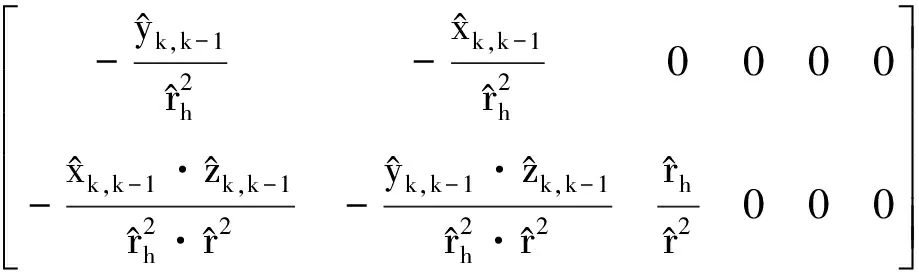
(7)

式中:

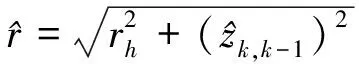
2.2 伪线性卡尔曼滤波

伪线性卡尔曼滤波使用伪线性测量残差来代替方位测量值。其特点是能够用线性估计理论求解纯方位TMA问题,且消除了EKF中滤波初值对算法稳定性的影响。其状态方程与(5)相同,观测方程为:

Z2k=h2(Xk)+V2k

(8)

式中：

(9)

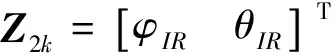
将观测方程(8)伪线性化后[2],得新的观测方程为:

Zk=HkXk+nk

(10)

式中：Zk=0,Hk=[Hk1,Hk2]:

Hk2=02×6

测量噪声nk=[rhvφIR,rvθIR]T的协方差阵为:

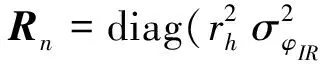
(11)

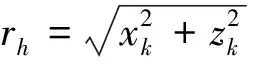
根据状态方程(5)和观测方程(10),并给定适当的初值,就可以用卡尔曼滤波对系统状态进行伪线性滤波。

2.3 基于修正球坐标系的角度跟踪算法

修正球坐标(MSC)中的卡尔曼滤波稳定且渐近无偏。其在修正的极坐标中建立数学模型,而算法仍采用EKF。

2.3.1 修正球坐标系

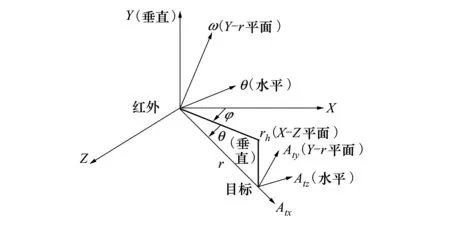
图1 修正的球坐标系

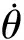
惯性坐标系(I)到目标视线坐标系(A)旋转矩阵为:

(12)

(13)

为便于描述,采用x1至x6依次表示X的对应分量,则:

(14)

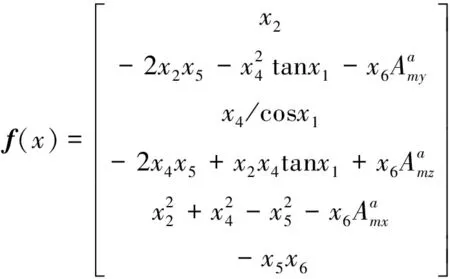
(15)

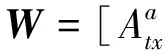
(16)

由(14)式和(15)式可以看出,当目标与红外传感器间的相对加速度为零时,前5个分量不受第6分量的影响,且第5分量可观测。只要存在加速度,该状态向量的分量全部可观测。在实际应用中,由于目标加速度通常未知,所以三方向加速度可当相互独立过程噪声处理。

2.3.2 基于MSC的卡尔曼滤波

将状态方程(13)式线性化得:

(17)

设红外传感器采样周期为T,则对上式离散化后所得的状态方程为:

Xk=Φk,k-1Xk+GkWk

(18)

式中：Φk,k-1=[Φ1,Φ2]

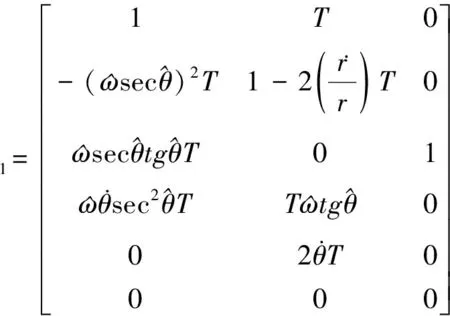
(19)

Φ2=

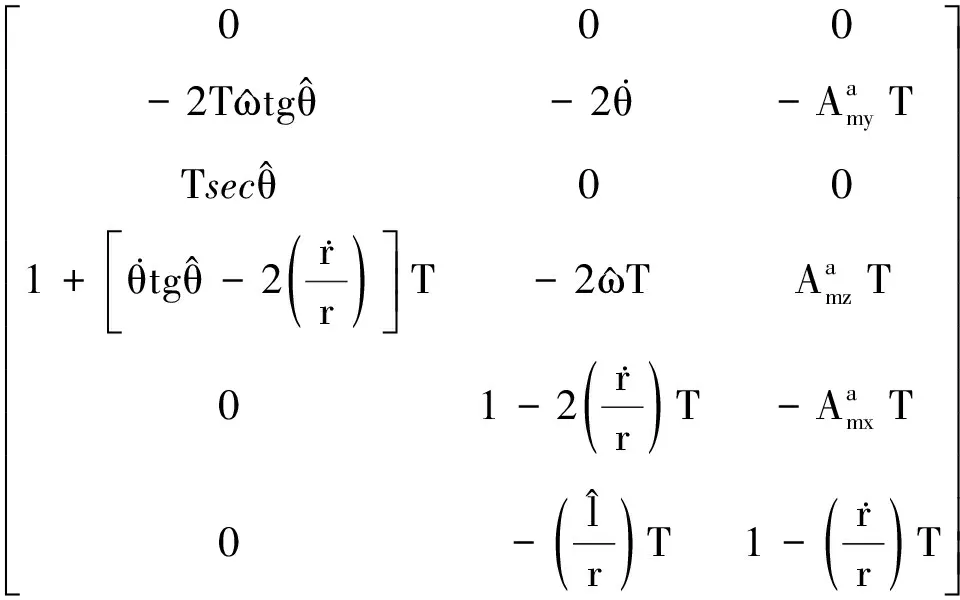
(20)

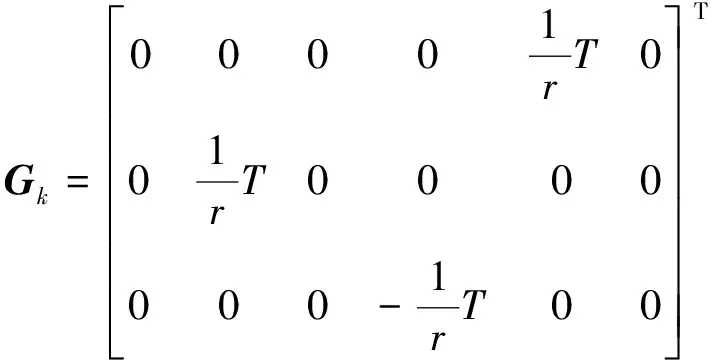
(21)

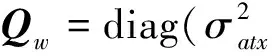
红外传感器的观测方程为：

Zk=HkXk+Vk

(22)

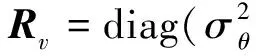
(23)

在得到离散状态方程、测量方程、过程噪声协方差阵和观测噪声协方差阵后,可得基于MSC的Kalman滤波方程组为:

(24)

式中:Pk|k-1为一步预测协方差阵,Pk为估计协方差阵,Kk为滤波增益阵。

(24)式在MSC中未进行状态外推。这是由于MSC中的非线性状态方程较为复杂,这时的外推过程本质上属于非线性滤波的外推。而在直角坐标系中却可以很容易地做到这一点,即目标的运动可以用相对简单的状态方程予以精确描述。所以,本文在MSC下进行状态更新,增益阵、滤波协方差以及预测协方差的计算,在并直角坐标系中进行外推。

值得注意的是,当由外推到滤波时,需要将目标在直角坐标系下的状态变为在MSC下的状态,由滤波到外推时,需要将目标在MSC下的状态变为直角坐标系下的状态。

(25)

可得:

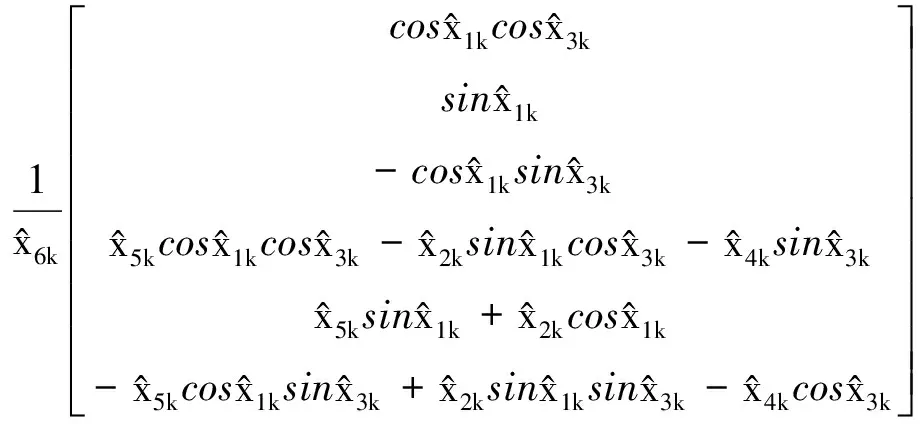
(26)

然后在直角坐标系中进行外推:

(27)

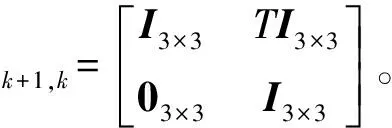
(28)

式中:

(29)

与EKF和PLE相比较而言,MSC坐标中的状态方程是非线性的,且远比直角坐标中复杂。然而,MSC滤波可将系统状态的可观测分量与不可观测分量自然分离,因此这种方法可以有效地抑制误差协方差阵的病态畸变。而直角坐标中的EKF滤波则无此特性,由此产生的估计误差的影响经常得出错误的可观测性,而MSC坐标中的EKF滤波则消除了以上直角滤波的缺陷,是一种稳定的滤波算法[5]。

3 仿真结果与分析

假定目标作匀速直线运动,采用红外导引头数据,对3种卡尔曼滤波算法进行仿真。数据设定为:扫描周期TIR为0.01 s。目标初始位置为(8 000,8 000,-8 000)m,运动速度为(340,0,0)m/s;导弹初始位置为(0,0,0)m,初始运动速度为(100,0,0)m/s,导弹在Y方向做S型机动。红外方位角、俯仰角的观测噪声标准差均为0.057°。分别采用随机设置初始状态的EKF、PLE和MSC下的EKF算法,通过Monte Carlo仿真实验,并选取100次收敛情况下得到的斜距估计误差随时间变化的结果。

图2和图3分别为位置滤波误差和速度滤波误差。由图可见,MSC滤波特性与理论分析一致。导弹机动时,估计值收敛,且滤波过程未出现不稳定的现象。伪线性滤波算法相对扩展卡尔曼滤波算法收敛较快,但随着时间的增加,其产生的有偏距离估计和速度估计是很明显的。

图4和5分别为俯仰角和方位角滤波误差曲线。可以看出,MSC滤波算法初始起伏较大,但随着迭代次数的增加,MSC滤波算法收敛到一个较高的精度。伪线性滤波算法和扩展卡尔曼滤波算法的收敛速度相当,但伪线性算法的估计精度略差。

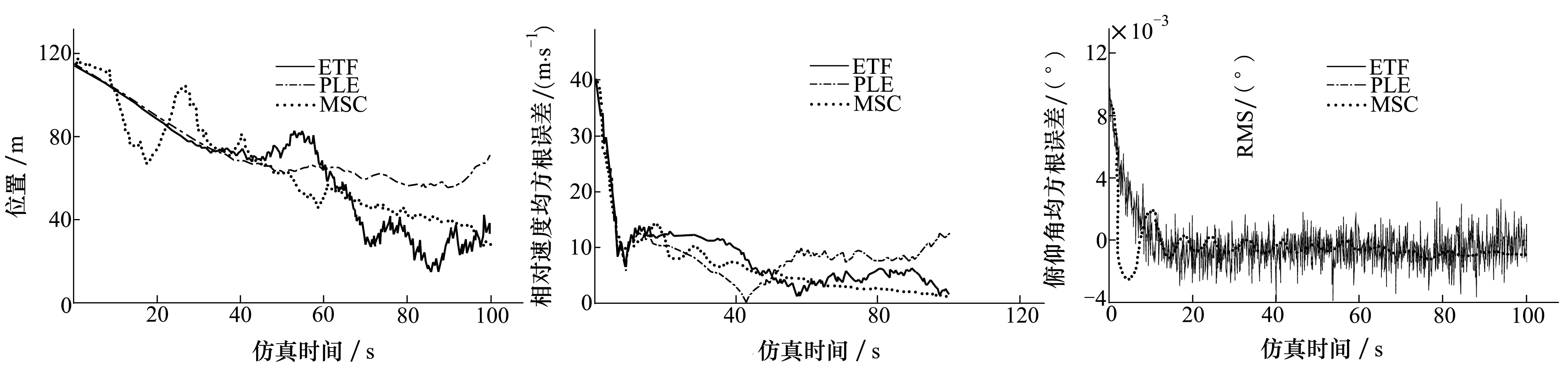
图2 位置滤波误差 图3 速度滤波误差 图4 俯仰角滤波误差

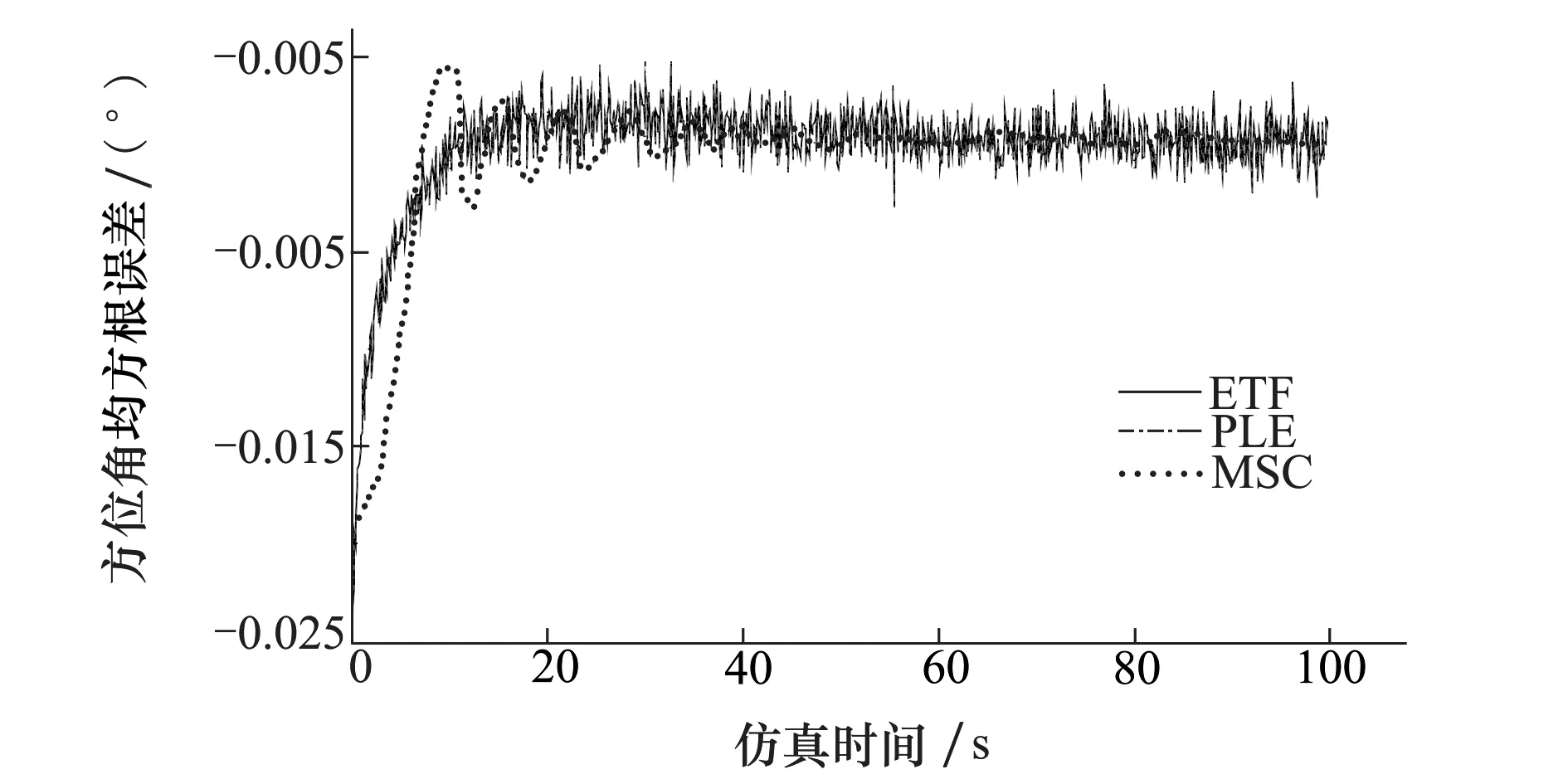
图5 方位角滤波误差

为比较各种算法的稳定性,通过100次Monte Carlo仿真实验,表1记录了3种算法收敛的次数。

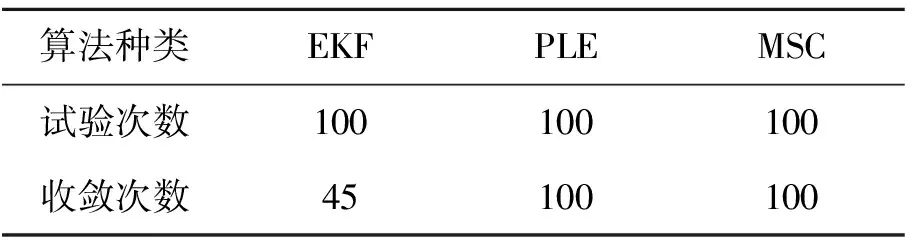
表1 3种算法收敛性能的比较

由表1可以看出,伪线性滤波算法和基于修正球坐标系的卡尔曼滤波算法的收敛性能要好于常规的扩展卡尔曼滤波算法。

4 结 论

本文结合工程实际,对红外纯方位TMA的卡尔曼滤波算法进行了详细的分析和比较,给出了可观测条件,分别用EKF、伪线性卡尔曼滤波和MSC下的EKF 3种滤波方法对纯方位TMA问题进行了求解。针对不同的算法给出了滤波方程,并对各方法的滤波特性进行了分析,并通过蒙特卡罗方法进行仿真验证。实验结果表明直角坐标中的EKF是一种不稳定的算法,算法容易发散;而伪线性卡尔曼滤波法虽然稳定性较好,但产生的估计是有偏的。MSC中的EKF,解决了算法的不稳定性问题,估计效果也相对较好。

参考文献：

[1] 修建娟, 孔博, 修建华. 基于伪线性和输入估计的无源自适应跟踪算法[J]. 信息与电子工程, 2011, 9(2):152-157

Xiu Jianjuan, Kong Bo, Xiu Jianhua. An Adaptive Tracking Algorithm Based on Pseudo-Linear and Input Estimation in Passive Location System[J]. Information and Electronic Engineering, 2011, 9(2):152-157 (in Chinese)

[2] 何友, 王国宏, 彭应宁,等. 多传感器信息融合及应用[M]. 北京:电子工业出版社,2000

He You, Wang Guohong, Peng Yingning, et al. Multisensor Information Fusion with Application[M]. Beijing: Electronics Industry Press, 2000 (in Chinese)

[3] 孙仲康, 郭福成, 冯道旺,等. 单站无源定位跟踪技术[M]. 北京:国防工业出版社,2008

Sun Zhongkang, Guo Fucheng, Feng Daowang. et al. Passive Location and Tracking Technology by Single Observer[M]. Beijing: National Defense Industry Press, 2008 (in Chinese)

[4] Aidala V J. Kalman Filter Behavior in Bearings-Only Tracking Applications. IEEE Trans on AES, 1979, 15(1): 29-39.

[5] 钟晓军, 王国宏, 陈士举, 蒋凤新. 伪线性滤波在导弹纯方位跟踪中的应用[J]. 飞航导弹, 2004, (5): 55-58

Zhong Xiaojun, Wang Guohong, Chen Shiju, Jiang Fengxin. Application of Pseudo Linear Filter in Bearings-only Tracking of Missile[J]. Winged Missiles Journal, 2004, (5): 55-58 (in Chinese)

[6] Aidala V J, Nardone S C. Biased Estimation Properties of the Pseudolinear Tracking Filter[J]. IEEE Trans on AES,1982, 18(4): 432-441

[7] 丁光庆, 冯新喜. 基于修正球坐标的红外目标跟踪[J]. 现代防御技术, 2007, 35(5): 101-104

Ding Guangqing Feng Xinxi. Target Tracking with Infrared Station Based on MSC[J]. Modern Defense Technology, 2007, 35(5): 101-104 (in Chinese)