多防线要地防空体系目标拦截能力评估
刘立佳,李相民,李 亮
(1.海军航空工程学院a.研究生管理大队;b.兵器科学与技术系;c.训练部,山东烟台264001;2.93246部队,长春130000)
研究防空系统与空袭武器的对抗过程,计算目标对防空系统的突防概率是分析防空火力网拦截能力的重要方面。自20世纪60年代排队论[1-2]成熟后,就应用到了防空系统拦击能力的分析领域。
随着预警机、空地导弹、制导炸弹等高科技武器的应用,现代防空作战模式发生了重大变化,依靠一种类型的防空武器很难对多种空袭武器实施有效拦截,需构筑多道防线对要地实施保护[3-5]。
实际应用中,由于受多种因素限制,不同方向上,多个防空武器杀伤区纵深不同,因而其拦截能力必然是关于方向变化的函数。而当前文献研究,多应用排队论将整个防空体系当做一个整体来计算其拦截能力[6-9],假设目标的来袭方向服从正态分布或以服从均匀分布的航路捷径进袭要地,而实际上,在某一方向内,目标从不同方位来袭的可能性不同,也不服从正态分布,以上假定同实际应用存在一定偏差。基于这一问题,本文利用插值算法来确定突防概率关于敌机来袭方向的函数曲线,从而得出防空火力网拦截能力的数学描述,作为评估防控火力网拦截能力的指标。仿真实验则说明本文提出的方法能够有效解决该问题。
1 现代防空作战多防线的划分
由于空袭兵器种类、战术多样,防空部署对空视界受作战环境的制约性,客观要求防空作战必须区分防御层次。
将远程防空武器防线部署至外围,拦截入侵的敌轰炸机、远程对地导弹,甚至是预警指挥机等目标,做到先发制人,这是至关重要的。
中程防空武器防线拦截突防远程防线的各类空中目标,其作战任务是将各类轰炸机拦截于投弹圈之外,使其不能完成投弹任务,而确保要地安全。
近程防线部署于要地周围,用来拦截突防的各类远程对地导弹及轰炸机投放的各类制导炸弹、导弹等,由于此类目标多低空突防目标,因而采用近程、低空防空武器予以拦截,具体请参见图1。由此可知,多防线防空武器部署拦截能力的评估问题,是当前防空武器作战使用的重要内容。
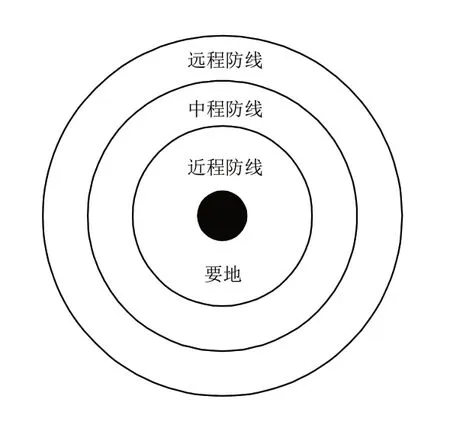
图1 防空武器防线划分示意图Fig.1 Schematic diagram of multi-air defending line
2 拦截能力评估的基本假设
设防御系统有3道防线,同防线上武器类型相同,不同防线上武器可以不相同。对不同防线上武器不同的防空系统,称为多防线异类防空系统[10]。
1)来袭目标为泊松流。其分布函数为

式中,λ为单位时间内来袭目标数量即泊松流强度。来袭目标流假设为泊松流是合理的,因为该流为最简单流,最难被防御系统拦截,将系统放在最难的情况下评估其拦截能力,必然高于实际情况[11]。
2)每个防空武器射击1次后,马上判断射击效果,若敌机被摧毁,则射击其他目标,否则继续对该敌机射击,直至其被击落或飞离防空武器杀伤区。这一时间间隔体现的统计特性用平均服务时间Tsev描述。μ=1/Tsev为单位时间内的服务率,防空系统(导弹,高炮)服务时间是由系统反应时间、射击次数以及每相邻2次射击之间的时间间隔决定,即

式(2)中:Tsev为服务时间;tr为系统反应时间;nf为对1个目标实施的射击次数;tf,i为第i、i+1次射击间隔时间,包括弹丸飞行时间、效果评估时间、决策时间。
由以上分析讨论可知,服务时间是1个阶梯函数,见图2。

图2 服务时间阶梯函数Fig.2 Step function of service time
可见,服务时间是一离散分布的随机变量。则

式中:P为单发毁伤概率;Tnf为射击nf次需要的时间。
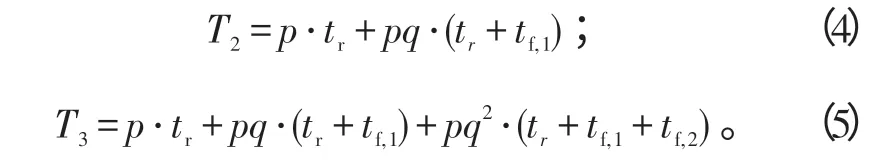
式(4)、(5)中:q=1-p;T2、T3为计算2次和3次射击需要的服务时间。
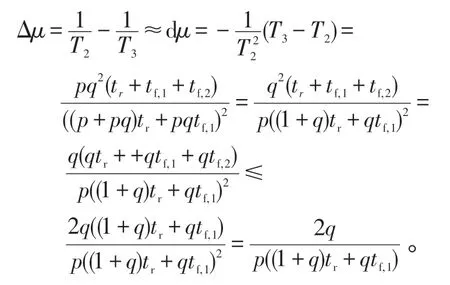
系统反应时间tr通常为10 s 左右时间,而对于中远程导弹系统而言,由于目标距火力单元可达数十千米,因而tf,1近1 min时间。有且可证明是关于q的增函数。对于精确制导武器来说q=1-p≤0.5,则有dμ是10-2数量级的。由以上推导可知,仅考虑2次射击所消耗的时间作为平均服务时间所产生的误差较小,因而当武器系统能够对杀伤区的目标完成2次以上射击时,平均服务率为
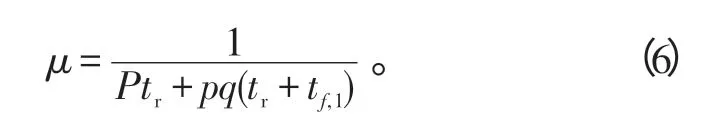
仅能满足1次射击时的服务率为

以上就是μ的确定方法。
3)若防空武器存在空闲发射单元,则当目标进入其杀伤区时,立即对其射击。
4)假设空袭目标直接进攻要地,不考虑目标同防空武器的对抗。
5)空袭目标按次序依次通过远程、中程、近程防空防线。
3 多防线防空武器系统拦截能力评估
根据第2节假设,空袭目标同防空武器系统之间具有典型的随机服务系统特征,构成了有限等待、多服务台、先来先服务的服务系统(M/M/C系统),具体请见图3。
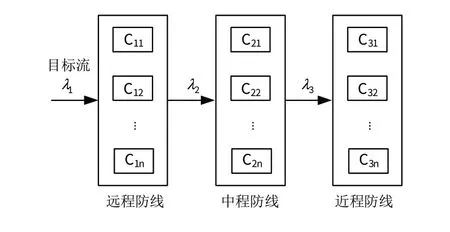
图3 多防线防空系统的排队系统示意图Fig.3 Queuing system schematic diagram of multi-air defending line
3.1 单防线突防概率计算
沿某方位φ 进袭的目标突防概率表达式如下:


式(9)~(12)中:λ为目标的到达强度;μ为火力单元的服务率;(υ为逗留率为目标飞行速度,d为目标在防空武器杀伤区内的飞行距离);C为能够对目标实施射击的防空武器数量,在多部防空武器杀伤区的重叠区域C >1,否则C=1。
3.2 多防线突防概率计算
设P突防(φ)i表示空袭目标以方位φ 突防第i 道防线的突防概率,突防该防线目标流强度记为λi,则

将λi代入式(3)~(7),就可得到P突防(φ)i。则目标突防多条防线后的突防概率为

3.3 突防概率关于来袭方位的函数
通过以上方法,可求得目标沿某方位φ 突防多防线防空系统的解析表达式,但目标可以在一个方位内,沿任意方位角进袭要地,当前一些文献假设φ 在可进袭的方位内服从均匀分布或正态分布,而求得空袭目标突防概率表达式。但实际上,目标沿某方位进袭要考虑到该方位是否有利于隐蔽、有利于瞄准、有利于逃逸等多方面因素,不一定服从正太分布或均匀分布。因此,本文采用拉格朗日插值来近似构造P突防关于来袭方位φ的表达式。
假设,经判断,敌机可能在方位θ1、θ2内进袭要地,且方位θ1、θ2内包含m个子方位,目标沿第j个方位来袭的可能性为为该方位的起始和终止角度,且有

设给定了l个方位来袭目标突防概率P突防(φk),其中k=1,2,…,l。则由拉格朗日插值得出
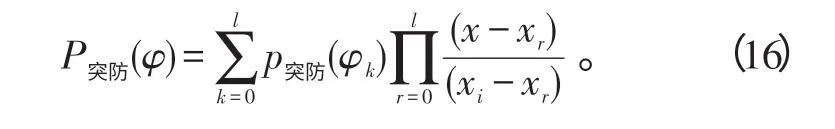
则p=min(P突防(φ))可用来衡量该多防线防空系统拦截能力。若考虑目标沿各方向来袭的可能性,也可用防线整体的突防概率均值作为衡量指标:

4 仿真实验
设要地由3个独立目标组成,各目标的重要性权重分别为0.6、0.1、0.3。根据各目标建筑强度,敌典型空地导弹对各目标的破坏半径分别为1.03 m、2.01 m和1.55 m,圆概率误差为2.05 m,导弹流为泊松流,强度4枚/min,持续时间10 min。防空武器采用扇形部署方式在要地外围的阵地纵深上形成远、中、近程防空防线,敌军可能从-60°~60°方向(以正北方向为准)来袭,具体请参见图4所示。
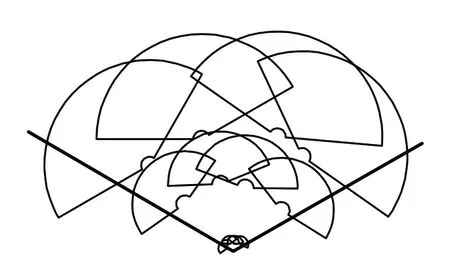
图4 防空阵地部署示意图Fig.4 Deployment schematic diagram of the air defense battle field
防空武器性能参数见表1。在-60°~60°范围内等分取7个来袭方位,解得目标通过3 条防线的突防概率见表2。应用以上数据得到插值后的函数P突防(φ)函数曲线见图5。

表1 各型防空武器性能参数Tab.1 Parameters of anti air weapons

表2 来袭方位及突防概率Tab.2 Attacking direction and penetration probability

图5 突防概率关于来袭方位函数曲线Fig.5 Penetration probability function curve of attacking direction
以上是由本文方法解得的结果。验证方法选用编程模拟目标流进攻要地,防空武器进行拦截的抗击过程。假设敌空地导弹分别从方位-30°、-10°、15°、40°以泊松流进袭要地,空袭时间持续10 min,以突防的目标数除以总的来袭目标数计算突防概率,最后结果为20次实验的平均值,见表3。

表3 模拟试验结果Tab.3 Test results
由此可以看出,模拟试验计算得到的突防概率平均值同来袭方向代入函数P突防(φ)的结果非常接近,这证明了本文提出的工程方法能够较好地作为评估防空网拦截能力。
5 结论
本文分析了多防线防空体系特点,给出了某方向来袭目标突防概率的解算,利用插值算法确定了突防概率同来袭方位的函数关系,来评估防控体系的拦截能力。仿真实验则进一步证明了本文提出的方法具备一定有效性。
[1]陆风山.排队论及应用[M].长沙:湖南科学技术出版社,1984:22-26.
LU FENGSHAN.Queuing theory and application[M].Changsha:Hunan Science and Technology Press,1984:22-26.(in Chinese)
[2]张最良,李长生.军事运筹学[M].北京:军事科学出版社,1993:34-41.
ZHANG ZUILIANG,LI CHANGSHENG.Military opearation research[M].Military Science Press,1993:34-41.(in Chinese)
[3]徐品高.现代国土防空末端防御防空导弹的关键技术[J].现代防御技术,2004,32(4):1-9.
XU PINGAO.The key technique of modern end defence missile for territory air defence[J].Modern Defence Technology,2004,32(4):1-9.(in Chinese)
[4]徐品高.三道防线是防空领域的重大军事变革[J].现代防御技术,2004,32(5):1-7.
XU PINGAO.A gand military revolution in the air defence area:three defensive lines[J].Modern Defence Technology,2004,32(5):1-7.(in Chinese)
[5]徐品高.用于要地末端防御的现代进程防空导弹需求分析[J].现代防御技术,2003,31(4):1-7.
XU PINGAO.Requirement analysis of modern short range air defence missiles for end defence[J].Modern Defence Technology,2003,31(4):1-7.(in Chinese)
[6]曹雷,董强,彭伟,等.基于排队论的导弹防御系统效能分析[J].南京理工大学学报,2011,35(4):470-474.
CAO LEI,DONG QIANG,PENG WEI,et al.Analysis of the missile defense system basing on queuing theory[J].Journal of Nanjing University of Science and Technology,2011,35(4):470-474.(in Chinese)
[7]贺川,王桂华,蒋里强,等.基于排队论的地空导弹武器系统作战效能评估[J].火力与指挥控制,2010,35(5):110-113.
HE CHUAN,WANG GUIHUA,JIANG LIQIANG,et al.The operation effectiveness assessment of the surface-toair missile weapon system based on queuing theory[J].Fire Control&Command and Control,2010,35(5):110-113.(in Chinese)
[8]郭建亮,高歆,申卯兴.基于排队论的多层拦截巡航导弹效率分析[J].空军工程大学学报,2009,10(5):37-40.
GUO JIANLIANG,GAO XIN,SHEN MAOXING.Analysis of intercept efficiency for multilayer defense cruise missile based on queuing theory[J].Journal of Air Force Engineering Universiry,2009,10(5):37-40.(in Chinese)
[9]郑春柏,鲁小强,康永文,等.排队论在地空导弹系统作战评估中的应用研究[J].舰船电子工程,2009,29(9):47-49.
ZHENG CHUNBO,LU XIAOQIANG,KANG YONGWEN,et al.Research and application of queuing theory in surface to air missile system appraising[J].Ship Electronic Engineering,2009,29(9):47-49.(in Chinese)
[10]卢发兴,吴玲,王航宇.多防线防御系统目标突防概率的计算[J].系统工程与电子技术,2005,27(6):1061-1065.
LU FAXING,WU LING,WANG HANGYU.Calculation of penetration probability of a target for a multi-line defense system[J].System Engineering and Electronics,2005,27(6):1061-1065.(in Chinese)
[11]郑泽席.多种防空武器混合部署时抗击效率的数学模型及方法[J].军事运筹与系统工程,2000(3):48-51.ZHENG ZEXI.Mathematic model multi-type anti air weapons intercept ability[J].Military System Engineering,2000(3):48-51.(in Chinese)
[12]许金余,赵德辉,宋洪斌.防空阵地网的理论及应用[M].西安:西北工业大学出版社,2005:12-24.XU JINGYU,ZHAO DEHUI,SONG HONGBIN.Theory and application of air defense bastion nets[M].Xi’an:Northwest Industrial University Press,2005:12-24.(in Chinese)

