飞机下滑波束导引系统设计及仿真

曲东才，谢曦鹏，曹 栋，冯玉光

（1.海军航空工程学院a.控制工程系；b.兵器科学与技术系，山东烟台264001；2.海军装备部，西安710089；3.海军航空兵学院，辽宁葫芦岛125001）

无线电波束导引系统是飞机广泛采用的制导系统，其中下滑波束导引系统是飞机在自动着陆时所采用的一种重要无线电波束导引系统。飞机在着陆前先在一定高度上作定高飞行（一般H=300～500 m），当截获下滑波束线后，即按一定下滑坡度下滑（一般θ=-2.5°～-3.0°）。由于此时飞机仍有较大速度（不低于失速速度的1.3倍），导致其垂直下降速度H˙亦较大（约H˙=-3.5～-4.5 m/s），达不到飞机安全接地要求（一般接地瞬间的H˙=-0.5～-0.6 m/s）[1-3]。因此，飞机下滑过程中需逐渐减小θ，使其沿下滑波束中心线下滑。可见性能良好的下滑波束导引系统可使飞机按要求的着陆姿态降落，最终精确导引飞机在着陆区安全着陆。

1 下滑波束导引系统工作原理

为导引飞机正确着陆，需要设置地面无线电信标台和由下滑耦合器、俯仰角位移控制系统等主要部件组成的下滑波束导引系统等机载无线电接收设备。

设置的地面无线电信标台包括航向信标台、下滑信标台，分别为飞机提供着陆基准；同时还设置外、中、近3 个地面指点信标台，以辨别几个监控点，确定飞机飞越其上空时刻，并在机上用灯光和音响信号的形式给出穿过指点信标台的信息。下滑信标台是在纵向平面内，通过向飞机着陆方向连续发射2 个不同频率（90、150 Hz）的高频无线电调幅波（其载波频率：329.3～335 MHz），进而形成下滑波束中心线（即等信号线，其仰角：2°～4°），为飞机在纵向平面内提供下滑基准[2-3]。航向信标台则在水平面内为飞机提供水平着陆基准。

机载下滑波束导引系统原理框图如图1 所示[2]。当飞机沿着下滑波束中心线飞行时，由于机载接收机接收到的2个频率信号强度相等，经解调、比幅后输出为0；但当飞机偏离下滑波束中心线时，就会产生波束偏差角ΔΓ，并经下滑耦合器，形成角位移指令信号Δϑg，送入俯仰角位移控制系统产生Δθ，迫使飞机回到下滑波束中心线，使其沿下滑波束中心线下滑。图1 中：Γg=0° 为给定的飞行轨迹参量，只要保证Γg=0°，飞机就沿着预定下滑波束中心线进场着陆。

图1 下滑波束导引系统原理框图Fig.1 Working principle of airborne slide beam guidance system

2 下滑波束导引系统设计

2.1 运动学环节

运动学环节及方程是描述飞机空间方位关系的，需建立飞机角运动量Δθ与轨迹运动参量ΔΓ之间的关系，进而构成下滑波束导引系统中的运动学环节。

设飞机沿下滑波束中心线以速度v0下滑，下滑波束中心线仰角为2.5°，飞机重心距离下滑信标台的斜距为R。当飞机受到干扰而偏离下滑波束中心线时，其飞机重心偏离的斜距R的垂直距离为d，并规定当飞机在波束中心线上方时d＞0。基于下滑运动的几何关系，即可由R与d决定偏差角Γ。由此可获得d˙、v0、θ满足[2，4-6]：

对式（1）拉氏变换并进行简单处理后可得

基于式（2），可建立运动学环节结构图见图2。

图2 运动学环节结构图Fig.2 Structure chart of kinematic link

2.2 下滑耦合器设计

基于上述运动学环节分析，为保证所设计的下滑波束导引系统具有良好的动态性能与稳态精度，除需合理选择控制规律并精心设计其传动比参数外，还要引入下滑耦合器等补偿环节对其进行补偿，使控制系统在接近地面时保持稳定。下滑耦合器如图3所示[2]。

下滑耦合器简要分析：①下滑耦合器比例＋积分的形式产生俯仰角位移控制指令Δϑg，以提高波束下滑导引系统的稳态精度。其中为耦合器的比例系数，为积分常数；②在耦合器中接入相位超前网络G(s)，以改善导引系统的动特性，

其零点s=-ωg1用来补偿俯仰角位移系统传递函数中最靠近坐标原点的极点；③通常耦合器应采取调参措施。

图3 下滑耦合器结构图Fig.3 Structure chart of slide coupler

2.3 下滑波束导引系统结构图的建立

基于以上分析和图1 下滑波束导引系统原理框图，可设计其下滑波束导引系统结构图见图4[2，7-9]。图4 中采用近似飞机短周期传递函数，并考虑垂风扰动及常值干扰力矩的作用。

图4 下滑波束导引系统结构图Fig.4 Structure chart of glide beam guidance system

3 仿真研究

3.1 仿真模型

图5 下滑波束导引系统仿真模型Fig.5 Simulation model of glide beam guidance system

基于图4，在Matlab 平台下，可建立相应的Simulink 仿真模型，如图5 所示[7-8]。在图5 中，由“pi”环节实现下滑耦合器的比例+积分形式，由“G(s)”环节实现相位超前网络G(s)，由环节“R”实现动态斜距R，其他同比例式自动驾驶仪控制规律设计[10-13]。

3.2 仿真分析

被控对象：某着陆状态下的喷气式运输机。飞行速度为v0=85.0 m/s，其短周期近似传递函数：

仿真初始值：舵回路时间常数0.1 s，航迹倾斜角θ0=-2.5°，斜距R=10 400 m，下滑线仰角2.5°；常值干扰力矩导致的干扰舵偏角Δδzr=0.15°，垂风干扰导致的干扰迎角Δαw=2.0°。通过仿真，获得在Γg=0°和Γg=1°两种情况下的仿真曲线如图6、7所示。

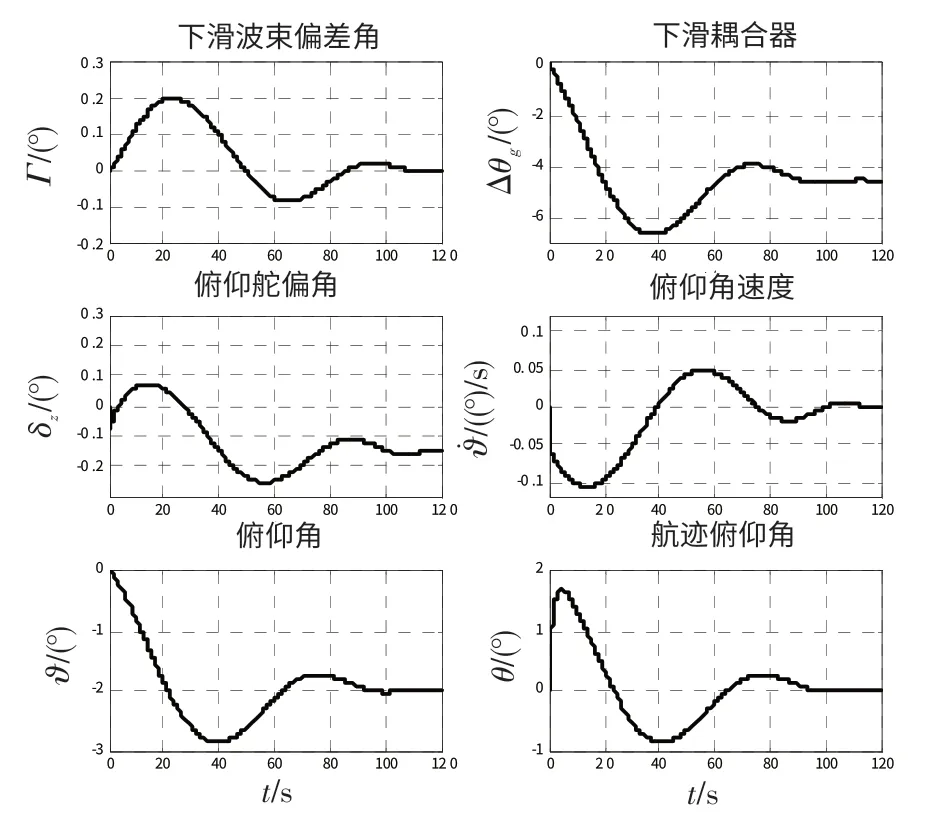
图6 下滑波束导引系统仿真曲线（Γg=0°）Fig.6 Simulation curve（Γg=0°）of slide beam guidance system

图7 下滑波束导引系统仿真曲线（Γg=1°）Fig.7 Simulation curve（Γg=1°）of slide beam guidance system

由仿真曲线可得：①在2 种典型干扰作用下，下滑波束偏差角Γ信号很好的跟踪了给定的指令Γg信号。Γ在100 s 后基本达到稳定，并具较高稳态精度；同时δz、ϑ、ϑ˙、θ等信号也逐渐趋于稳定状态，但系统在跟踪给定指令Γg=1°信号时，显然比Γg=0°的舵偏角δz要付出更大能量，其剧烈程度也更大；②通过合理设置下滑耦合器pi 控制器参数及相位超前网络G(s)，使耦合器所提供的零点近似补偿了原点处一个极点1/s的作用，同时G(s)所提供的零点s=-0.5 也近似补偿控制系统的一个1/s=-0.5 的极点，使控制系统趋稳定，并增大了系统的稳定裕度。

4 结论

本文在简要分析下滑波束导引系统工作原理基础上，建立飞机下滑波束导引系统结构图，并在MATLAB 平台下，仿真选取下滑耦合器参数、角位移控制系统传动比。通过仿真曲线可见，所设计的下滑耦合器等参数是合适的，其下滑波束导引系统结构是合理的。需要注意的是：对于飞机的运动学环节，若飞机原始速度向量精准对准下滑线，即θ0=-2.5°的情况下，Δθ将以积分形式使Γ角越来越大，这意味着随飞机接近地面，积分速率v0/R趋于无穷大，导引系统必将发散（实际上这也是各种导引系统的一般规律）。为改善控制系统的稳定性，因而需要精心设计下滑耦合器参数；同时对于运动学环节中的斜距R，在飞机下滑着陆的动态过程中是以R=R0-v0t变化的，而不能作为常数而“冻结”；pi控制器参数应可随R自动调节，以便保持开环增益在下滑过程中基本不变。

[1] BRIAN L S，FRANK L L.Aircraft control and simulation[M]. Hoboken，New Jersey：John Wiley & Sons. Inc.，1992：109-114.

[2] 张明廉. 飞行控制系统[M]. 北京：国防工业出版社，1984：268-282.

ZHANG MINGLIAN. Flight control system[M]. Beijing：National Defense Industry Press，1984：268-282（in Chinese）

[3] 文传源.现代飞行控制[M].北京：北京航空航天大学出版社，2004：143-196.

WEN CHUANYUAN.Modern flight control[M].Beijing：Beihang University Press，2004：143-196.（in Chinese）

[4] CHRISTOPHER FIELDING，et al. Advanced techniques for clearance of flight control laws[M]. Berlin：Sprinter，2002：180-205.

[5] NIEWOEHNER R J，KAMINER I.Design of an autoland controller for an F-14 aircraft using H-infinity control[J].Journal of Guidance，Control and Dynamics，1996，19（3）：656-663.

[6] SHYH PYING S，AGARWAL R K. Design of automatic landing systems using mixed H2/H∞control[J]. Journal of Guidance，Control and Dynamics，1999，22（1）：103-114.

[7] 高冰，李鹏，张学，等.基于自适应模糊控制的飞机自动着陆系统[J].电气传动，2011，41（8）：24-27.

GAO BING，LI PENG，ZHANG XUE，et al.Airplane automatic landing system based on adaptive fuzzy conrtol[J].Electric Drive，2011，41（8）：24-27.（in Chinese）

[8] 袁锁中，陶德桂.自动着陆系统μ综合控制研究[J].南京航空航天大学学报，2003，35（2）：184-188.

YUAN SUOZHONG，TAO DEGUI. μ synthesis control in automatic landing system[J]. Journal of Nanjing University of Aeronautics &Astronautics，2003，35（2）：184-188.（in Chinese）

[9] 刘冰，艾剑良.基于LQG/LTR方法的飞机自动着陆系统设计[J].动力学与控制学报，2010，8（1）：92-96.

LIU BING，AI JIANLIANG. Design of an aircraft autolanding system based on the LQG/LTR method[J]. Journal of Dynamicsand Control，2010，8（1）：92-96.（in Chinese）

[10]苏希尔·古普塔.控制系统基础[M].北京：机械工业出版社，2004：248-291.

SUDHIR GUPTA. Elements of control systems[M]. Beijing：China Machine Press，2004：248-291.

[11]侯博涵.航空飞行自动控制系统性能分析[J].现代电子技术，2003，26（9）：38-39.

HOU BOHAN.Performance analysis of aviation flight automatic control system[J]. Modern Electronics Technique，2003，26（9）：38-39.（in Chinese）

[12]程继红，曲东才.某型飞机角位移自动驾驶仪比例式控制规律设计与仿真[J].海军航空工程学院学报，2011，26（3）：241-245.

CHENG JIHONG，QU DONGCAI. Design and simulation of the proportional control law for aircraft angular displacement autopilot[J]. Journal of Naval Aeronautical and Astronautical University，2011，26（3）：241-245.（in Chinese）

[13]赵广元.Matlab与控制系统仿真实践[M].北京：北京航空航天大学出版社，2009：199-203.

ZHAO GUAGNYUAN. Emulation study of Matlab and control system[M]. Beijing：Beihang University Press，2009：199-203.（in Chinese）