非线性模型预测控制的研究进展

赵国荣，盖俊峰，胡正高，刘文宝

（1.海军航空工程学院a.控制工程系；b.研究生管理大队，山东烟台264001；2.93132部队，黑龙江齐齐哈尔161016）

模型预测控制（Model Predictive Control，MPC）是一种在工业过程控制领域得到成功应用的控制策略。由于直接产生于实际工业过程控制，且全面考虑了工业实际需求，具有较高的综合控制质量，因而MPC自其诞生之日起便吸引了众多研究者的目光，并逐渐引起了工业控制界和理论界的重视。迄今为止，模型预测控制已被广泛应用于发电、炼油、冶金、化工、汽车、航天等领域。MPC 作为一种新兴的控制理论能得到如此成功应用，其主要原因可总结为：

1）通过滚动优化策略在线求解局部最优问题。模型预测控制是一种动态优化方法，通过优化窗口的滚动，对模型预测输出值和实际输出值进行比较，再通过反馈校正实现系统输出对参考值的跟踪。由于MPC 采用有限时域优化窗口，仅需求解局部最优问题，大大减少了优化计算量。同时，反馈校正可解决系统干扰等不确定性问题。

2）直接处理约束条件的能力。模型预测控制通过在线优化求解控制律，在其在线优化过程中，可以全面考虑各种约束条件（如状态约束、输入约束、输入增量约束、输出约束等），从而得出既能使优化指标最优又能满足各种约束条件的控制律，这是传统的PID控制和经典最优控制理论所无法实现的。

上述2 个特点使得MPC 更接近实际的工业生产控制过程，因而得到了众多工程技术人员和研究者的青睐。

预测控制自诞生至今，在工程实践和理论研究方面都取得了重大进展[1-6]。本文由模型预测控制的基本原理入手，对非线性模型预测控制的基本思路进行了说明；对目前该领域的热点问题和取得的成果进行了综述；从当前的需求展望该领域，提出了其研究应该加强的几个方面的问题。

1 非线性模型预测控制的理论基础

1.1 非线性模型预测控制的基本原理

模型预测控制发展至今，出现了若干不同类型的算法。但这些不同算法的基本原理是相同的，包括如下3项基本内容[1]：

1）预测模型。MPC 是一种基于预测模型的控制算法，根据对象系统的历史信息和未来控制输入，利用预测模型对系统的未来输出进行预测。预测模型的结构形式是多样的，状态方程、传递函数、阶跃响应、脉冲响应和一些非线性系统、分布参数系统的模型，都可以作为MPC的预测模型。

2）滚动优化。MPC是一种优化控制算法，与经典最优控制理论并无本质区别。但MPC 是一种有限时域的滚动优化，不是像传统最优控制那样采用一个对全局都相同的优化性能指标，而是在每一时刻都有一个特定的优化性能指标，在每一个优化时域内进行在线滚动优化。滚动优化是MPC 区别于经典最优控制的基本特点。

3）反馈校正。MPC 是一种闭环控制算法。在通过滚动优化确定了下一个控制时域内的控制作用序列后，并不是将此控制序列全部作用于系统，而仅实现当前时刻的控制作用。到下一时刻，根据对象系统的实际输出，利用预测模型对系统进行新的预测，然后基于此开始新一轮的优化。反馈校正能有效防止模型失配和系统干扰引起的控制作用对理想状态的偏离，使MPC构成闭环优化。

总之，模型预测控制是一种基于预测模型、进行滚动优化并结合反馈校正的优化控制策略。其基本原理如图1所示。

图1 MPC的基本原理Fig.1 Basic principle of MPC

下面以离散时间非线性系统为例，进一步介绍非线性模型预测控制（NMPC）的基本原理。考虑如下的离散时间非线性系统：

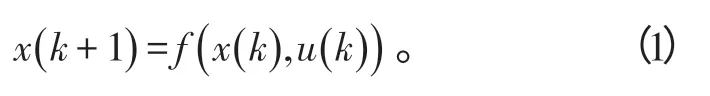
式（1）中：x∈ℝn为系统状态；u∈ℝm为系统输入，k=0,1,…为采样时刻；f(∙ ,∙)为非线性函数，且有f( 0,0)=0。假设原点为系统（1）的平衡点，且状态完全可测。

考虑系统（1）的状态约束和输入约束如下：

式（2）中：X和U分别为包含原点的凸集，且满足X和U都为紧的。基于状态空间模型（1）的非线性模型预测控制的基本结构如图2所示。其中，N为预测步长，x(i|k)和u(i|k)为k时刻对未来第k+i时刻预测的状态和输入变量。

考虑带有约束条件（2）的系统（1），则NMPC的基本问题可定义为以下的有限时域最优控制问题（Finite Horizon Optimal Control Problem，FHOCP）：

式（3）中：目标函数J(x)为有限时域N内的控制性能函数，通常为定义在原点某邻域内的非负连续函数，且有J( 0)=0；V(k)为最优性能指标函数，一般称为值函数；x(k)∈X为系统在当前时刻k的状态。在非线性模型预测控制的基本定义中，J(x)通常为有限个正定函数之和。在任一采样时刻k，定义FHOCP在线优化控制变量u(k;N)为

一般情况下，取控制域Nc小于预测域Np，即0 ＜Nc＜Np。

若上述FHOCP 优化可行，可得最优控制序列u*(k;N)，仅将该最优控制序列的第一项u*( 0|k)作用于实际控制系统；在下一采样时刻k+1，用系统状态x(k+1) 作为FHOCP的初始状态，重复优化执行过程，直到采样过程结束。以上介绍的就是NMPC 实现滚动优化控制的基本原理。

1.2 非线性预测控制的无穷时域近似方法

考虑离散时间非线性系统（1）。在k时刻由x(k)出发的无穷时域最优控制问题的性能指标可描述为

而模型预测控制通常在有限时域内进行优化，其性能指标可描述为

比较式（5）和式（6）可得

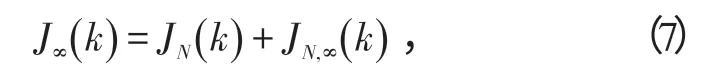
由上述分析可知，要将模型预测控制的有限时域优化问题近似为无穷时域的最优控制问题，必需对有限时域后的无穷时域部分进行补偿。对于这个问题，常见的方法有3种，下面分别进行介绍。

1.2.1 带有终端零约束（等式约束）的NMPC

对MPC的滚动时域控制引入终端零约束的思想，最早是由Kwon等在文献[7]中提出的。文献[8-9]又将此思想应用到了广义预测控制（Generalized predictive control，GPC）中，提出了终端零状态约束的GPC 算法。文献[10]提出了一种基于终端零约束的NMPC算法。考虑系统（1），具有终端零约束的NMPC 优化问题可描述为：

式（8）中：x( 0,x0)=x0，x0为优化起始点；N为预测步长。

终端零约束是对系统未来状态的一种估计，即在预测时域后的系统状态都为零。此方法虽能保证系统稳定，但对无穷时域的近似却比较保守且条件苛刻。

1.2.2 带有终端代价函数的NMPC

文献[11]将终端零约束进行了松弛化处理，针对无约束线性系统引入终端加权方法保证系统的稳定性，其实质是为MPC控制时域后的无穷时域性能指标给出了一个上界，这也是具有终端代价函数的NMPC的基本思想。具有终端代价函数的NMPC 的优化问题可描述为：

式（9）中：F(∙)为终端代价函数，且满足F( 0)=0 ，F(x)≥α( ‖x‖)，α(∙)为K类函数；F(x(N,x0))满足

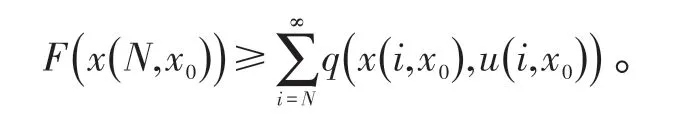
终端代价函数是对终端零约束的一种扩展，相比于终端零约束，此方法对无穷时域的近似具有更低的保守性，且应用条件更为宽松。

1.2.3 带有终端集约束的NMPC

带有终端集约束的NMPC 方案是与双模控制方案一起出现的。文献[12]针对一类有约束的非线性系统，将终端零约束用终端集代替，提出了双模预测控制方案。双模控制方案是对无穷时域最优控制进行近似的一种预测控制策略，是一种对后来的研究工作产生重要影响的控制思想。带有终端集约束的NMPC优化问题可描述为：

式（10）中：Xf为终端状态约束集，简称终端集，是包含原点的闭集。此类问题通常采用双模控制结构，当状态在Xf外时，采用有限时域滚动控制，在此有限时域内，将系统状态驱动到终端集Xf内；当系统状态进入Xf内后，则采用局部线性反馈控制律对其进行控制。实际上，终端状态集约束与终端代价函数约束一样，也是终端零约束的一种扩展。一般来说，把系统的状态驱动到一个集合内要相对容易，因而具有终端集约束的NMPC 方案比具有终端零约束的NMPC 方案的保守性更低，也可较好地对无穷时域最优化进行近似。

2 非线性模型预测控制的研究进展

模型预测控制理论的发展经历了2 个主要阶段。第1个阶段通常称为经典预测控制理论阶段。在此期间，针对工业界在实际中的需求，提出了若干预测控制算法，如动态矩阵控制（Dynamic Matrix Control，DMC）[13]、模型算法控制（Model Algorithmic control，MAC）[14]、内模控制（Internal Model Control，IMC）[15]、预测函数控制（Predictive Funetional Control，PFC）[16]和广义预测控制（Generalized Predictive Control，GPC）[17]，等等。自上世纪90年代中期以来，学术界掀起了对模型预测控制研究的新一轮高潮，通常将这一时期称为模型预测控制理论发展的第2 阶段，即现代预测控制的综合理论阶段。在此阶段，以文献[6]为代表，涌现出了大量具有重要意义的学术成果。本节着眼于模型预测控制发展的第2 阶段，以近年出现的具有代表性的理论研究成果为主，对预测控制相关领域热点问题的研究进展进行简要介绍。

2.1 基于线性近似的非线性模型预测控制研究

非线性系统预测控制的关键问题在于如何处理非线性和降低在线计算量。在线性系统控制问题中，已经发展出多种成熟的数学方法，如Fourier变换、Laplace 变换、叠加原理，等等。但对非线性系统进行分析和设计控制器时，上述数学工具都不再适用。因此，对于实际工程人员和理论研究者来说，处理非线性系统最直接也是最有效的办法是将系统的非线性特性线性化，然后再用成熟的线性系统设计方法完成控制过程[18]。在这一思路下，工业界和理论界出现了一批基于线性近似方法的非线性模型预测控制算法。1984年，Garcia 在文献[19]中首次提出了应用线性化方法的非线性预测控制方案，并在实际工业过程中进行了应用。文献[20]在文献[19]方法的基础上增加了一个扩展Kalman 滤波器以改善扰动估计，并能较好地处理不稳定过程动态特性。1987年，Costas 提出了全局反馈线性化的思想[21]。文献[22]提出了基于递归神经网络全局反馈线性化的广义预测控制方案，文献[23]提出了基于全局反馈线性化的预测函数控制器，并进行了工业应用研究。文献[24]用中值定理将非线性系统进行线性化处理，并对线性系统的时变参数进行逼近。文献[25]针对只含输出非线性环节的系统用Taylor 级数一阶展开近似线性化，但是该方法不能处理含有输入非线性环节的系统。运用Taylor级数展开法对非线性系统进行线性近似时，要求表征系统模型的输入输出函数必须连续可微。文献[26]指出，利用Stirling 插值公式对非线性函数进行线性化处理的精度要高于Taylor 一阶近似，且不需对其进行求导运算，因而对不满足连续可微假设的非线性系统，Stirling插值公式依然适用。上述文献进行预测控制器设计时，为了降低在线计算量，通常忽略了线性化过程中产生的非线性高阶项。

2.2 具有终端代价函数的非线性模型预测控制研究

在1.2.2节中已经提到，终端代价函数是对终端零约束的一种扩展，相比于终端零约束，此方法对无穷时域的近似具有更低的保守性，且应用条件更为宽松。因此，具有终端代价函数的非线性模型预测控制方法成为近年来研究的热点。终端代价函数对NMPC的控制性能起着十分重要的作用，终端代价函数的选取对增大系统的吸引域、降低全局性能指标的消耗都具有积极意义。文献[27]提出了一种经济性模型预测控制方法，引入了一个广义代价函数来实现控制目标。文献[11]用伪代数Riccati方程作为终端代价函数，保证了系统的稳定性。文献[28]针对一类无终端状态约束的模型预测控制，证明了按比例增大终端代价函数会相应的增大预测控制的吸引域。文献[29]采用支持向量机拟合的方法，为一类离散时间非线性系统生成了终端代价函数，并保证了系统的渐进稳定性。文献[30]采用一个二次型终端代价函数，对系统进行有限时域优化，同时指出只要选取适当的参数便可保证系统的稳定性，但未明确给出参数的选取规则，以及不同参数对系统性能指标的影响。

2.3 非线性时滞系统模型预测控制研究进展

现代工业控制过程主要存在2 大难题：对象系统的非线性问题和时滞问题。实际控制过程中的对象系统绝大部分为非线性系统，而且往往无法用准确的模型进行描述；而时滞现象广泛存在于工业控制系统中，如核反应系统、微波发生器、涡轮喷气机、轧制系统、长管道进料系统等等。通常情况下，时滞能使系统的性能变坏，甚至引起系统的不稳定。从理论研究的角度来看，时滞现象给系统稳定性分析及控制器设计带来了很大困难[31]。由于时滞系统能引起对象系统的不稳定，因而针对时滞系统的模型预测控制必须研究其稳定性，而不是仅将预测时域进行调整，使其大于时滞常数就可以了[1]。早期关于时滞系统的模型预测控制方法很少考虑对系统的约束条件，没有充分体现出模型预测控制算法的优势。Kothare 等[32]针对输入受限的时滞系统给出了基于LMI 约束的预测控制思路，但并没有得出具有实际意义的结果，正是由于系统时滞的存在以及模型的不确定性。

针对时滞系统的模型预测控制的研究大多以状态空间模型为研究对象，其主要原因可总结为2点：首先，在处理多变量问题上，状态空间模型与基于输入输出关系的传递函数相比具有明显的优越性；其次，目前对非线性系统进行稳定性分析的最佳工具为基于状态空间的Lyapunov 稳定性理论[6]。鉴于上述原因，目前的研究成果绝大部分是基于状态空间描述的模型。由于模型预测控制在工业过程中能有效地处理约束条件，因而开展考虑约束的时滞系统模型预测控制方法研究具有重要的理论和工程应用意义。文献[33]针对一类凸多面体不确定时滞系统，进行了鲁棒模型预测控制算法研究。文献[34-35]针对时滞常数未知的凸多面体不确定系统，分别提出了相应的模型预测控制算法。文献[36]针对具有复杂时滞的系统，提出了一种状态反馈预测控制方法，利用状态变量值在预测时域内保持不变的假设推导出了适合工程应用的预测控制算法。近年来，针对非线性时滞系统的预测控制得到了学者们的进一步研究[37-41]。Reble等在文献[42-45]中研究了非线性连续时滞系统模型预测控制中的稳定性和次优估计问题，提出了时滞系统模型预测控制的次优性指标等概念。

2.4 基于LMI的鲁棒模型预测控制研究进展

随着模型预测控制方法与理论的日趋成熟，对于不确定对象的鲁棒模型预测控制的研究成为当前预测控制领域的热点问题。鲁棒预测控制的实质是在线求解一个关于系统未来状态和输入的min-max优化问题。在现有的研究成果中，不确定系统一般分为基于扰动模型的受扰系统和基于多胞模型的参数不确定系统。而更为普遍的研究对象是采用多胞模型描述的不确定系统。相比于扰动模型，多胞模型的适用性更广，非线性系统和时变系统在特定的条件下都可以转化为多胞模型描述的不确定系统。对于多胞模型描述的不确定系统，线性矩阵不等式（Linear Matrix Inequalities，LMI）成为鲁棒预测控制器设计的重要工具。1996年，Kothare等在文献[32]中率先提出了针对多胞不确定系统的鲁棒预测控制器设计方法。该方法基于椭圆不变集理论，由min-max原理出发，通过对目标性能函数上界进行优化，将鲁棒预测控制问题转化为由LMI描述的优化问题：

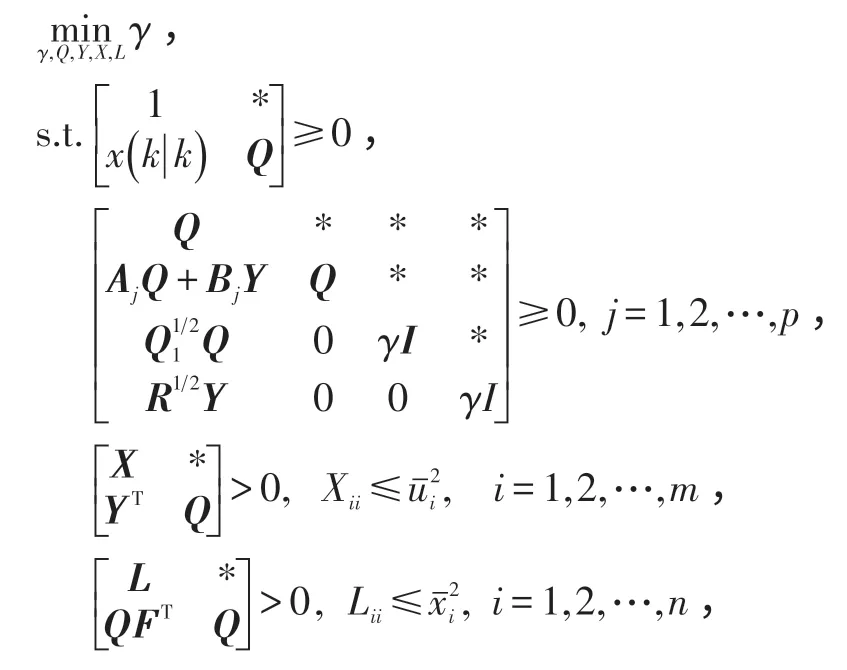
式中，*表示对称矩阵中相应的对称项。

上述第2个不等式表示采用反馈增益YQ-1时，多胞各顶点模型中的无穷时域优化性能指标上界均能保证为γ。第3和第4个不等式分别描述了系统的输入约束和状态约束。

文献[32]为后来采用LMI方法设计鲁棒预测控制器及处理约束条件的研究奠定了基础。Cuzzola 等[46]基于文献[32]，针对用多胞模型描述的线性时变系统，通过设计参数依赖Lyapunov 函数降低了文献[32]中方法的保守性。而Mao[47]通过纠正文献[46]中关于不变集的设计错误，完善了该方法。文献[48]用LMI 方法设计了一种高效鲁棒预测控制器，在性能分析的基础上提出了改善鲁棒预测控制次优性的方法。近年来，针对不确定时滞系统鲁棒预测控制的研究也取得了若干成果[49-50]。其中，文献[50]针对一类多胞模型描述的不确定时滞系统，提出了一种带有时滞补偿的时滞相关鲁棒模型预测控制方法。将难以求解的minmax优化问题转化为带有LMI约束的凸优化问题，设计了能保证闭环系统稳定的鲁棒模型预测控制器，并证明了其控制算法的可行性。文献[51]针对非线性系统中不确定性问题设计了模型预测控制器。Cannon等在文献[52]中通过把非线性对象系统模型转化为多胞描述模型，进而采用高效鲁棒预测控制方法研究了其模型预测控制问题。

3 对非线性模型预测控制研究的展望

非线性模型预测控制无论是理论还是应用都远未成熟，这主要是因为非线性系统及其约束优化问题都不能用参数化的形式统一表达。近年来，预测控制定性综合理论的发展虽然为非线性约束预测控制带来了不少新的思路，但与实际应用尚有距离。从目前应用领域对其的需求来看，应该加强以下方面的研究：

1）进一步开展基于线性近似的模型预测控制算法。在该部分的研究工作中，是否有更适合应用在非线性模型预测控制中的线性近似方法，是需要进一步探讨的问题。另外，在对线性近似所产生高阶项进行逼近的过程中，应寻求优秀的非线性逼近方法，以进一步减少非线性模型预测控制的在线计算量。

2）进一步研究具有终端代价函数的非线性模型预测控制问题。目前所见的研究成果中的终端代价函数大多是固定的，终端代价函数不能随着控制过程的推进而进行适当的调整，这不利于增大吸引域和降低全局性能指标消耗。因此，具有自调节终端代价函数的预测控制理论及其工程应用问题是进一步研究的方向。

3）进一步开展针对时滞系统的模型预测控制问题的研究。目前针对时滞系统的非线性模型预测控制算法大多需要构造Lyapunov 函数来保证系统的渐近稳定，这无疑增加了计算量。寻求非线性时滞系统模型预测控制的新思路和新方法，是值得进一步研究的问题。另外，现有文献在对多胞时滞系统进行鲁棒预测控制研究时，通常假设系统状态实时可测，这与很多工程实践是不相符的。因此，考虑系统状态不可直接测量的情况，开展具有输出反馈的鲁棒模型预测控制算法研究具有一定的现实意义。

综上所述，预测控制的研究应该着力克服理论与应用的脱节，针对各应用领域的需求，发展既有理论保证、又能满足应用环境和实时性要求的高效算法，为各行各业解决约束优化问题提供理论依据充分、实用性强、兼顾优化与稳定等性能要求的系统理论和算法，并以此推动预测控制理论的进一步发展，这是预测控制研究始终追求的目标，也是预测控制未来发展的方向。

4 结束语

在过去的近20年里，非线性模型预测控制取得了长足的进步。通过采用对无穷时域优化的近似，较好地解决了非线性模型预测控制稳定性保证和性能优化的问题。许多具有性能保证的预测控制器设计方法相继提出，为非线性模型预测控制的实际应用提供了理论基础。如何设计同时具有良好控制性能，较大初始可行域和较小在线计算量的高效非线性模型预测控制器，成为近年来研究的热点，这是一个需要继续研究的课题。而在基本非线性模型预测控制理论日渐成熟的基础上，进一步考虑状态观测器、系统参数辨识以及多速率采样等情况，也必将产生更多具有挑战性的问题。

[1] 席裕庚.预测控制[M].北京：国防工业出版社，1993：4-6.

XI YUGENG. Predictive control[M]. Beijing：National Defense Industry Press，1993：4-6.（in Chinese）

[2] 席裕庚，李德伟.预测控制定性综合理论的基本思路和研究现状[J].自动化学报，2008，34（10）：1225-1234.

XI YUGENG，LI DEWEI. Fundamental philosophy and status of qualitative synthesis of model predictive control[J]. Acta Automatica Sinica，2008，34（10）：1225-1234.（in Chinese）

[3] 席裕庚，李德伟，林姝.模型预测控制—现状与挑战[J].自动化学报，2013，39（3）：222-232．

XI YUGENG，LI DEWEI，LIN SHU. Model predictive control—status and challenges[J]. Acta Automatica Sinica，2013，39（3）：222-232.（in Chinese）

[4] 何德峰，丁宝苍，于树友.非线性系统模型预测控制若干基本特点与主题回顾[J]. 控制理论与应用，2013，30（3）：273-287.

HE DEFENG，DING BAOCANG，YU SHUYOU. Review of fundamental properties and topics of model predictive control for nonlinear systems[J]. Control Theory and Applications，2013，30（3）：273-287.（in Chinese）

[5] GARCIA C E，PRETT D M，MORARI M.Model predictive control：theory and practice—a survey[J]. Automatica，1989，25（3）：335-348.

[6] MAYNE D Q，RAWLINGS J B，RAO C V，et al. Constrained model predictive control：Stability and optimality[J].Automatica，2000，36（6）：789-814.

[7] KWON W H，PEARSON A E. On feedback stabilization of time-varying discrete linear systems[J]. IEEE Transactions on Automatic Control，1978，23（3）：479-481.

[8] SCOKAERT P O M，CLARKE D W. Stabilizing properties of constrained predictive control[J]. IEEE Proceedings：Control Theory and Applications，1994，141（5）：295-304.

[9] CLARKE D W，SCATTOLINI R. Constrained recedinghorizon predictive control[J]. IEEE Proceedings：Control Theory and Applications，1991，138（4）：347-354.

[10] KEERTHI S S，GILBERT E G.Optimal infinite-horizon feedback laws for a general class of constrained discretetime systems：stability and moving-horizon approximations[J]. Journal of Optimization Theory and Applications，1988，57（2）：265-293.

[11] BITMEAD R R，GEVERS M，WERTZ V.Adaptive optimal control：the thinking man’s GPC[M]. New Jersey：Prentice-Hall，1990：157-173.

[12]MICHALSKA H，MAYNE D Q.Robust receding horizon control of constrained nonlinear systems[J]. IEEE Transactions on Automatic Control，1993，38（11）：1623-1633.

[13] CUTLER C R，RAMAKER B L. Dynamic matrix control—a computer control algorithm[C]//Proceedings of the Joint Automatic Control Conference. San Francisco，USA：AACC，1980.

[14] ROUHANI R，MEHRA R K. Model algorithmic control（MAC）：basic theoretical properties[J]. Automatica，1982，18（4）：401-414.

[15]GARCIA C E，MORARI M.Internal model control：a unifying review and some new results[J]. IEC Process Des.Dev.，1982，21（2）：308-323.

[16]KUNTZE H B，JACUBASCH A，RICHALET J，et al.On the predictive functional control of an elastic industrial robot[C]//Proceedings of 25th CDC. Athens，1986：1877-1881.

[17] CLARKE D W，MONHTADL C，TUFFS P S. Generalize predictive control—Part I. the basic algorithm[J]. Automatica，1987，23（2）：137-148.

[18]胡跃明，胡终须，毛宗源，等.非线性控制系统的近似化方法[J].控制理论与应用，2001，18（2）：160-165.

HU YUEMING，HU ZHONGXU，MAO ZONGYUAN，et al. Approximation methods of nonlinear control systems [J]. Control Theory and Applications，2001，18（2）：160-165.（in Chinese）

[19] GARCIA C E. Quadratic dynamic matrix control of nonlinear process. an application to a batch reactor process[C]//AIChE Annual Meeting.San Francisco，1984.

[20] LEE J H，RICKER N L. Extended Kalman filter based nonlinear model predictive control[J]. Ind. Eng. Chem.Res.1994，33：1530-1541.

[21] COSTAS K，CHANG BOCK CHUNG. Nonlinear state feedback synthesis by global input/output linearization[J].AIChE Journal，1987，33：592-603.

[22] ZHONG X，WANG S Q. Constrained predictive control with recurrent neural network based feedback linearization[C]//IIGSS the third workshop.1998：107-111.

[23]张新民，荣冈.间歇反应过程的预测函数控制[J].信息与控制，1999，28（增刊）：102-106.

ZHANG XINMIN，RONG GANG. Predictive fundamental control of nonlinear batch process[J]. Information and Control，1999，28（S）：102-106.（in Chinese）

[24]郭健，陈庆伟，朱瑞军.一类非线性系统的自适应预测控制[J].控制理论与应用，2002，19（1）：68-72.

GUO JIAN，CHEN QINGWEI，ZHU RUIJUN. Adaptive predictive control of a class of nonlinear systems[J].Control Theory and Applications，2002，19（1）：68-72.（in Chinese）

[25] MARTIN RAU，DIERK SCHRODER. Model predictive control with nonlinear state space models[C]//IEEE，AMC 2002-Maribor.Slovenia，2002：136-141.

[26]王亚锋，孙富春，张友安，等.一种跟踪问题中的次优非线性预测控制算法[J].控制与决策，2009，24（11）：1682-1686．

WANG YA FENG，SUN FUCHUN，ZHANG YOUAN，et al.Suboptimal model predictive control for nonlinear system on tracking problem[J]. Control and Decision，2009，24（11）：1682-1686.（in Chinese）

[27]ANGELI D，AMRIT R，RAWLINGS J B.On average performance and stability of economic model predictive control[J].IEEE Transactions on Automatic Control，2012，57（7）：1615-1626.

[28] LIMON D，et al. On the stability of constrained MPC without terminal constraint[J]. IEEE Transactions on Automatic Control，2006，51（6）：832-836.

[29] ONG C J，SUI D，GILBERT E G. Enlarging the terminal region of nonlinear model predictive control using the support vector machine method[J]. Automatica，2006，42（6）：1011-1016.

[30] PARISINI T，ZOPPOLI R.A receding horizon regulator for nonlinear systems and a neural approximation[J].Automatica，1995，31（10）：1443-1451.

[31]刘桂萍，武俊峰，王世明.模糊预测控制在非线性时滞系统中的应用[J].哈尔滨理工大学学报，2010，15（2）：24-34.

LIU GUIPING，WU JUNFENG，WANG SHIMING. The application of fuzzy predictive control for nonlinear timedelay systems[J].Journal of Harbin University of Science and Technology，2010，15（2）：24-34.（in Chinese）

[32] KOTHARE M V，BALAKRISHNAN V，MORARI M.Robust constrained model predictive control using linear matrix inequalities[J]. Automatica，1996，32（10）：1361-1379.

[33] LIU Z L，ZHANG J，PEI R，et al. Robust model predictive control of time- delay systems[C]//Proceedings of 2003 IEEE Conference on Control Applications. 2003，23-25（1）：470-473.

[34] HU X B，CHEN W H. Model predictive control for constrained systems with uncertain state-delays[C]//International Journal of Robust Nonlinear Control. 2004：1421-1432.

[35] JEONG S C，PARK P. Constrained MPC for uncertain time-varying systems with state-delay[J]. IEEE Transactions on Automatic Control.2005，50（2）：257-263.

[36] XIA YUANQING，JIA YINGMIN. Robust sliding mode control for uncertain time-delay system：an LMI approach[C]//Proc.ACC.Anchorage.2002：53-58.

[37] HEIDARINEJAD M，LIU J，CHRISTOFIDES P D. Economic model predictive control of nonlinear process systems using Lyapunov techniques[J]. AIChE Journal，2012，58：855-870.

[38] GRAICHEN K，KUGI A. Stability and incremental improvement of suboptimal MPC without terminal constraints[J]. IEEE Transactions Automatic Control，2010，55（11）：2576-2580.

[39] 李妍，毛志忠，王福利，等. 基于分段Lyapunov 函数的Hammerstein-Wiener 非线性预测控制[J].控制与决策，2011，26（5）：650-654.

LI YAN，MAO ZHIZHONG，WANG FULI，et al. Hammerstein- wiener nonlinear predictive control based on piecewise lyapunov function[J]. Control and Decision，2011，26（5）：650-654.（in Chinese）

[40] GRUNE L，PANNEK J. Nonlinear model predictive control：theory and algorithms[M]. London：Springer，2011：256-268.

[41] GRUNE L，PANNEK J，SEEHAFER M，et al. Analysis of unconstrained nonlinear MPC schemes with time varying control horizon[J]. SIAM Journal on Control and Optimization，2010，48（8）：4938-4962.

[42] REBLE M，ALLGOWER F. Unconstrained nonlinear model predictive control and sub-optimality estimates for continuous-time systems[C]//Proceedings of 18th IFAC World Congress.Milan，Italy，2011：6733-6738.

[43] REBLE M，MULLER M. A，ALLGOWER F. Unconstrained model predictive control and suboptimality estimates for nonlinear time-delay systems[C]//Proceedings of 50th IEEE Conference of Decision Control and European Control Conference.Orlando，FL，USA，2011：7599-7604，.

[44] REBLE M，MAHBOOBI ESFANJANI R，NIKRAVESH S K Y，et al.Model predictive control of constrained nonlinear time-delay systems[J]. IMA Journal of Mathematical Control and Information，2011，28（2）：183-201.

[45] REBLE M，BRUNNER FD，ALLGOWER F. Model predictive control for nonlinear time-delay systems without terminal constraint[C]//Proceedings of 18th IFAC World Congress，Milan，Italy，2011：9254-9259.

[46] CUZZOLA F C，GEROMEL J C，MORARI M. An improved approach for constrained robust model predictive control[J].Automatica，2002，38（7）：1183-1189.

[47] MAO W J. Robust stabilization of uncertain time-varying discrete systems and comments on“an improved approach for constrained robust model predictive control”[J].Automatica，2003，39（6）：1109-1112.

[48] CANNON M，KOUVARITAKIS B. Optimizing prediction dynamics for robust MPC[J]. IEEE Transactions on Automatic Control，2005，50（11）：1892-1897.

[49] SANTO WIJAYA，MANOP WONGSAISUWAN. Robust MPC for PWA with time-delay systems using saturated linear feedback controller[C]//Computer and Automation Engineering（ICCAE）.2010.

[50]李善强，石宇静，陈东彦，等.凸多面体不确定时滞系统鲁棒模型预测控制[J].哈尔滨理工大学学报，2011，16（4）：108-117.

LI SHANQIANG，SHI YUJING，CHEN DONGYAN，et al. Robust model predictive control for time-delay systems with polytopic uncertainty[J].Journal of Harbin University of Science and Technology，2011，16（4）：108-117.（in Chinese）

[51] RUBAGOTTI M，RAIMONDO D M，FERRARA A，et al. Robust model predictive control with integral sliding mode in continuous-time sampled-data nonlinear systems[J]. IEEE Transactions on Automatic Control，2011，56：556-570.

[52] CANNON M，KOUVARITAKIS B，LEE Y I，et al. Efficient nonlinear model predictive control[J]. International Journal of Control，2001，74（4）：363-372.