机载雷达目标跟踪与航迹信息提取

兰 天，程继红

（1.海军装备部西安军事代表局，太原030006；2.海军航空工程学院科研部，山东烟台264001）

机载雷达航迹信息提取是当前信息化综合作战、传感器组网作战和多平台一体化联合作战的重要研究课题[1]。在对这一问题的研究中，航迹信息提取的关键在于如何实现目标的精确跟踪。针对这一情况，文献[2]基于几何学的原理设计了多传感器目标协同跟踪模型，并通过对目标速度精度的分析，有效提高了远距离目标跟踪的精度；文献[3]依据自动特征尺度提取理论，通过目标特征点尺度的变化对目标的跟踪精度做出了进一步的提高；文献[4]借助随机集理论，不仅在一定程度上避免了数据关联步骤的困扰，还使目标数未知的多目标跟踪精度得到了有效的提高。然而上述文献的研究并没有对多目标情况下目标机动[5]时的情况加以充分考虑。在现代战场环境下，目标数目并不单一、且不可能始终以编队直线的方式运动。因此，复杂多变的目标运动轨迹不可避免地会对目标跟踪带来较大的影响，进而严重干扰目标航迹信息的提取。

本文提出一种ECEF坐标系下基于交互多模型的多机协同跟踪算法。通过对ECEF坐标系下多目标跟踪模型的协同交互，目标机动时的跟踪精度和航迹信息提取精度得到了有效的提高。

1 机载雷达目标跟踪

1.1 跟踪坐标系的选取

机载雷达的初始量测数据是在载体坐标系下得到的，具体包括载体坐标系下的距离、方位角、俯仰角和径向速度等。而机载雷达的跟踪坐标系一般选用大地直角（ECEF）坐标系[6-7]，因而在对目标跟踪滤波前，要将载体坐标系下的量测数据转换到跟踪坐标系，其坐标转换示意图如图1所示。

图1 机载雷达目标跟踪坐标系转换示意图Fig.1 Coordinate system change schematic diagram of airborne radar target tracking

1.2 ECEF坐标系下的目标量测

假设机载雷达的量测为距离r(k)、方位角θ(k)和俯仰角ε(k)。那么，载体坐标系下的测量方程为

式中：vr(k)、vθ(k)和vε(k)分别为具有0 均值、恒定方差的高斯量测噪声。

为有效实现对目标的精确跟踪，NED坐标系[8-9]下的目标无偏转换量测为

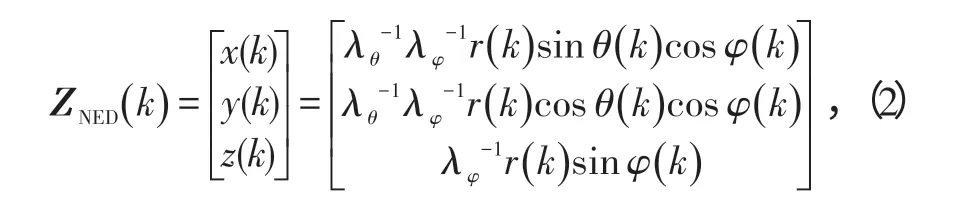
式中：λθ=λφ=。

进而ECEF坐标系下的目标量测为

式中：M(k)表示NED坐标到ECEF坐标的旋转矩阵；ZO(k)为ECEF坐标系下机载雷达的位置量测。

1.3 交互多模型目标跟踪

在获得目标量测模型的基础上，拟采用交互多模型[10-12]的方法来实现对目标的精确跟踪，其具体步骤如下。

步骤1：状态估计的交互。

假设共有N个滤波器模型，且对于第j个模型滤波器，计算其混合的目标状态估计X0j(k|k)和混合的协方差矩阵P0j(k|k)：

式（4）、（5）中：

其中，pij为从模型i 到模型j的转移概率。

[13]胡志丁、曹原、刘玉立、葛岳静：《我国政治地理学研究的新发展：地缘环境探索》，《人文地理》2013年第5期。

步骤2：条件模型更新。

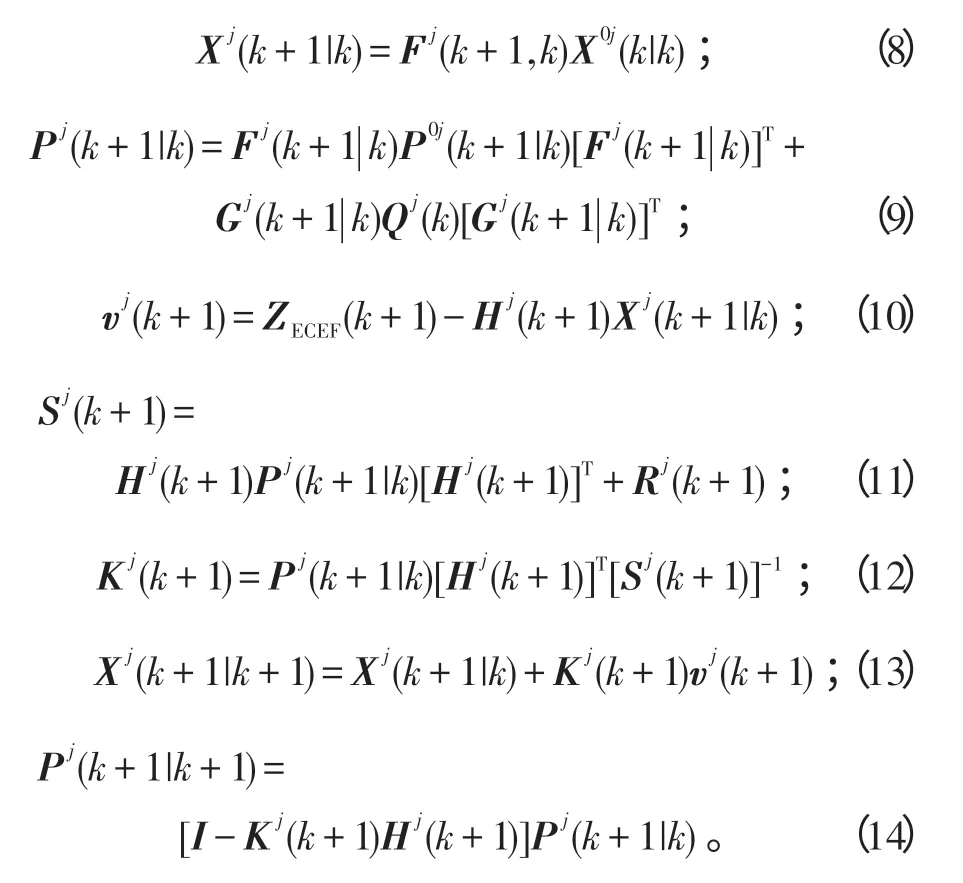
式（8）～（14）中：Xj(k+1|k)是在模型j 下的预测状态估计；相应的预测协方差矩阵为Pj(k+1|k)；vj(k+1)是新息；Sj(k+1)是新息协方差矩阵；Kj(k+1)是滤波增益；Xj(k+1|k+1)是在模型Mj(k+1)下的状态更新估计；P(k+1|k+1)是得到更新的协方差矩阵。

步骤3：各模型的似然函数的计算。

步骤4：模型概率更新。

模型j的概率更新计算为

式中，归一化因子

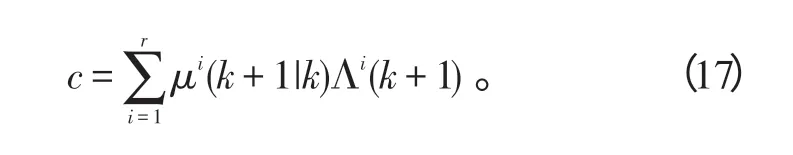
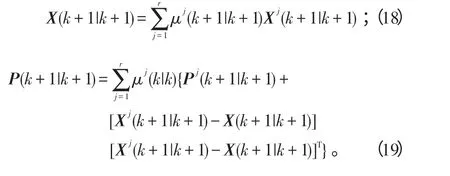
1.4 航迹融合

在获得各载机对目标状态估计的基础上，假设不同机载雷达对目标的状态估计和协方差分别为、P1(k|k)和P2(k|k)，那么融合后的结果为

式中，

2 机载雷达航迹信息提取

由于各种测量噪声以及飞机自身运动噪声的影响，机载雷达测量对目标状态的估计值通常起伏很大。针对这一情况，拟采用2次滤波的技术来实现目标航迹信息的提取，其具体步骤如下。

1）从当前时刻开始往前取N个测量值（N为奇数，根据需要可以取3、5、7、9等）。

2）对这N个测量值按从小到大的顺序进行排序。

3）取排序后的第(N+1) 2个数值（大小位于中间的值）作为估计值。

在第N次测量之前，所有测量值按奇次测量时刻和偶次测量时刻分别采用如下方法处理。

①对奇数测量时刻，则按上述方法取中值作为估计值。

②对偶数测量时刻，取不出中值，此时取中间两个值的平均值作为估计值。

3 仿真分析与结论

假设3 部机载雷达对5个目标进行协同跟踪，并以ECEF坐标系为融合中心进行数据处理。目标以编队的形式做转弯运动。机载雷达的测距误差为15 m，方位和俯仰测量误差为0.1°，跟踪时间100 s。在上述条件下，进行了100次Monte-Carlo仿真，本文提出的基于交互多模型的航迹信息提取结果与文献[2]所提算法的分析比较如图2～7所示。

图2为目标量测图，图3为ECEF坐标系下各机载雷达对目标的融合跟踪误差图。由图2、图3可以看出：机载雷达对目标实现了较为稳定的融合跟踪，跟踪误差可以收敛到50 m 以下，且本文所提出的ECEF坐标系下基于IMM的融合跟踪算法相对于文献[2]中的方法有着较好的跟踪效果。

图2 目标量测图Fig.2 Target measurements

图3 目标状态估计均值Fig.3 Means of target state estimate errors

图4～7分别为目标的航速信息、航向信息、角速度信息和角加速度信息提取图。可以看出：采用本文提出的基于交互多模型的航迹信息提取算法可得到较为精确的目标航迹信息；3 部机载雷达对目标的融合航迹信息相对于各机载雷达要相对较好，且相对于文献[2]中的方法具有更加稳定的提取结果。

图4 航速均方根误差Fig.4 Velocity RMSE

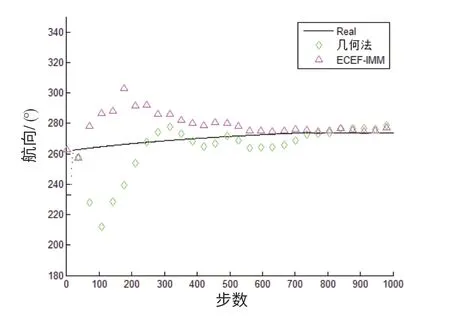
图5 航向均方根误差Fig.5 Course RMSE

图6 角速度均方根误差Fig.6 Angular speed RMSE

图7 角加速度均方根误差Fig.7 Angular acceleration RMSE

4 结束语

本文就远距离机动目标跟踪的问题进行了深入的研究，提出了一种ECEF坐标系下基于交互多模型的多机协同跟踪算法，并同单个机载雷达的跟踪结果相比进行了仿真分析。仿真结果表明，本文所提的ECEF坐标系下基于交互多模型的多机协同跟踪算法有着较高的目标跟踪精度和航迹信息提取精度。因此，研究ECEF坐标系下基于交互多模型的多机协同跟踪有着重要的意义。

[1]HE Y，WANG G H，LU D J，et al.Multisensor information fusion with applications[M].Beijing：Publishing House of Electronics Industry，2007：167-194.

[2]叶继坤，雷虎民，薛东风，等.基于几何关系的多弹协同跟踪算法[J].系统工程理论与实践，2012，32（10）：2332-2334.

YE JIKUN，LEI HUMIN，XUE DONGFENG，et al.Multiple missiles cooperative tracking algorithm base on geometric relation[J].Systems Engineering Theory and Practice，2012，32（10）：2332-2334.（in Chinese）

[3]董蓉，李勃，陈启美.基于局部不变特征点数据集的目标跟踪算法[J].仪器仪表学报，2012，33（9）：2053-2055.

DONG RONG，LI BO，CHEN QIMEI.Object tracking algorithm based on dataset of local invariant feature points[J].Chinese Journal of Science Instrument，2012，33（9）：2053-2055.（in Chinese）

[4]陈金广，马丽丽.基于随机集理论的多目标跟踪研究进展[J].光电工程，2012，39（10）：16-18.

CHEN JINGUANG，MA LILI.Development of multi-target tracking methods based on random finite set[J].Opto-Electronic Engineering，2012，39（10）：16-18.（in Chinese）

[5]刘钦，刘铮，刘俊.一种多机动目标协同跟踪的博弈论算法[J].西安电子科技大学学报，2012，39（6）：50-54.

LIU QIN，LIU ZHENG，LIU JUN.Collaborative tracking algorithm for multiple maneuvering targets based on the game theory[J].Journal of Xidian University，2012，39（6）：50-54.（in Chinese）

[6]崔亚齐，熊伟，何友.基于MLR的动平台传感器误差配准算法[J].航空学报，2012，33（1）：118-128.

CUI YAQI，XIONG WEI，HE YOU.Mobile platform sensor registration algorithm based on MLR[J].Acta Aeronautica et Astronautica Sinica，2012，33（1）：118-128.（in Chinese）

[7]CHEN L，WANG G H，JIA SY，et al.Attitude bias conversion model for mobile radar error registration[J].Journal of Navigation，2012，65（4）：651-670.

[8]JENKINS K L，CASTANON D A.Information-based Adaptive Sensor Management for Sensor Networks[C]//Proceedings of American Control Conference.2011：4934-4940.

[9]THURAIAPPAH S，TAT J C，SANJEEV A，et al.A multiple hypothesis tracker for multitarget tracking with multiple simultaneous measurements[J].IEEE Journal of Selected Topics in Signal Processing，2013，7（3）：448-459.

[10]彭冬亮，郭云飞，薛安克.三维高速机动目标跟踪交互式多模型算法[J].控制理论与应用，2008，25（5）：831-836.

PENG DONGLIANG，GUO YUNFEI，XUE ANKE.An interacting multiple model algorithm for a 3D high maneuvering target tracking[J].Control Theory and Applications，2008，25（5）：831-836.（in Chinese）

[11]HE X F，THARMARASA R，KIRUBARAJAN T.Modified murty’s algorithm for diverse multitarget top hypothesis extraction[J].IEEE Transactions on Aerospace and Electronic Systems，2013，49（1）：603-609.

[12]XU Z H，LI Y，RIZOS C，et al.Novel hybrid of LS-SVM and Kalman filter for GPS/INS integration[J].Journal of Navigation，2010，63（2）：289-299.