基于粒子滤波的跟踪算法研究

， ，

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

非线性滤波问题是运动目标跟踪研究领域的关键问题，近年来引起越来越多研究者们的关注。在目标模型为非线性时，通常采用扩展卡尔曼滤波器(EKF)[1-2]对其进行跟踪。它的基本思路是对运动目标的非线性模型在状态向量的邻域内做Taylor展开，取其一阶或二阶近似。然而，该算法需要计算模型的Jacobian矩阵，因而计算复杂，实现起来较为困难。而且，在模型的非线性较强以及系统噪声非高斯时，EKF的估计精度严重降低，并可能造成滤波器的发散[3]。基于上述EKF在非线性系统中的问题，近年来提出了粒子滤波[4-5]跟踪算法。粒子滤波也叫做贝叶斯滤波(Bayes filter)或蒙特卡罗滤波 (Monte Carlo filter)，它是一种蒙特卡罗方法[6]。该算法通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差分布。本文通过仿真实验研究了噪声协方差与粒子数对PF的影响，并将PF与EKF进行了对比。实验结果表明，当运动模型为强非线性时，PF比EKF具有更小的均方根误差( RMSE)和更高的目标跟踪精度。

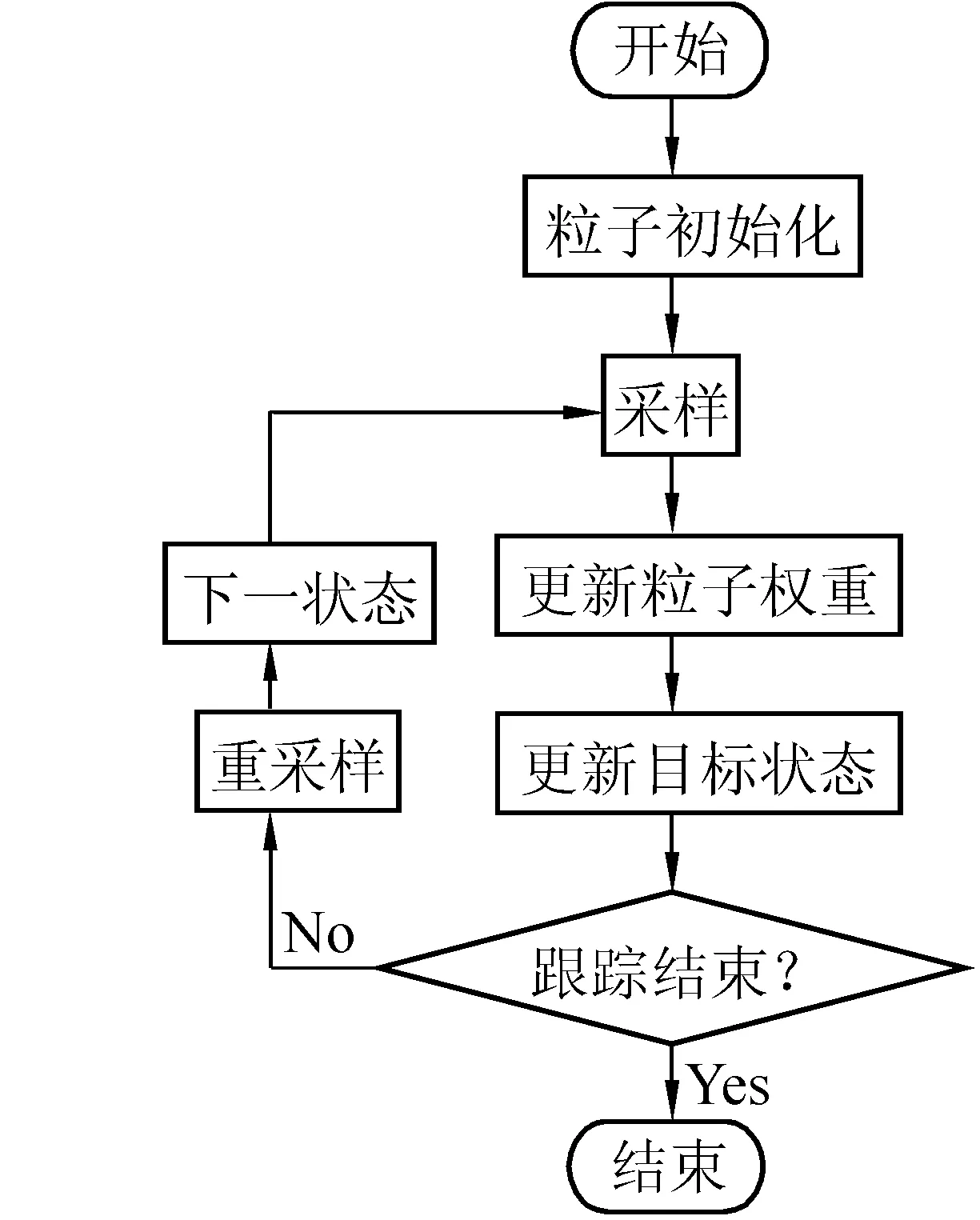
图1 粒子滤波跟踪算法流程图

1 粒子滤波跟踪算法

粒子滤波跟踪算法可用于强非线性系统。其流程图如图1所示。

粒子滤波跟踪运动目标的具体算法如下[7]：

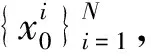
第二步：采样。通过系统状态转移方程

xk=f(xk-1,uk) (1)

(2)

式中，q(xk|x0:k-1,uk)为概率密度分布近似目标函数p(xk)。

第三步：更新粒子权重。通过观测方程

yk=h(xk,vk) (3)

(4)

式中，yk表示k时刻实际观测值。然后将粒子权值进行归一化处理

(5)

此时可以通过式(2)近似计算出后验概率密度分布

(6)

(7)

第六步：下一状态重复第二步并循环迭代。

2 目标跟踪仿真实验及分析

2.1 扩展卡尔曼滤波器和粒子滤波器性能对比

采用广泛使用的非线性模型，分别使用扩展卡尔曼滤波器和粒子滤波器完成了运动目标跟踪实验，实验结果和误差分析如图2所示。非线性模型

图2 EKF与PF状态估计仿真实验

(8)

式中，wk,vk均为零均值的高斯白噪声，其方差分别为Q=1和R=1。初始粒子分布为均值为0，方差为2的正态分布，时间步长数为50。粒子滤波的粒子数为100，蒙特卡洛仿真次数为200次。

由图2(a)可以看出，当运动模型是强非线性时，扩展卡尔曼滤波器对目标跟踪的偏差非常大，在时间长度为50 s的蒙特卡罗迭代中，几乎有1/5的目标估计状态与真实状态有明显偏差，有的甚至与真实状态完全相反。而粒子滤波器基本上可以准确估计目标的状态，没有出现估计状态与目标真实状态相反的情况，仅仅与真实值有很小的偏差。为了从定量的角度来对比EKF和PF在强非线性下的运动目标跟踪误差，本文进一步计算了两种方法的状态估计均方根误差RMSE及其均值。图2(b) 为仿真过程中两种方法的状态估计均方根误差曲线，并求得出EKF的RMSE均值为4.828 3，PF的RMSE均值为0.775 32。从以上分析结果可以看出，PF中的RMSE相对于EKF得到了显著地降低，PF中的RMSE均值降低为EKF的16%，PF的估计性能明显优于EKF。

2.2 粒子数和噪声协方差对粒子滤波跟踪算法的影响

在粒子滤波跟踪算法中，过程噪声与观测噪声协方差分别影响着目标预测和观测值，进而影响算法中每个粒子的权值，最终使滤波结果受到影响；粒子数代表着算法中样本的大小，样本越多，越能够反映运动目标的真实状态。本实验通过调整噪声协方差的值与粒子数的大小，来观察这些因素对粒子滤波跟踪算法的影响。非线性系统模型如式(1),式(2)所示，用粒子滤波跟踪算法对上述非线性系统的状态进行估计。图3是过程噪声与观测噪声协方差均为1，粒子数分别取值N=20、50、100、200时，用PF进行目标状态估计的实验结果。

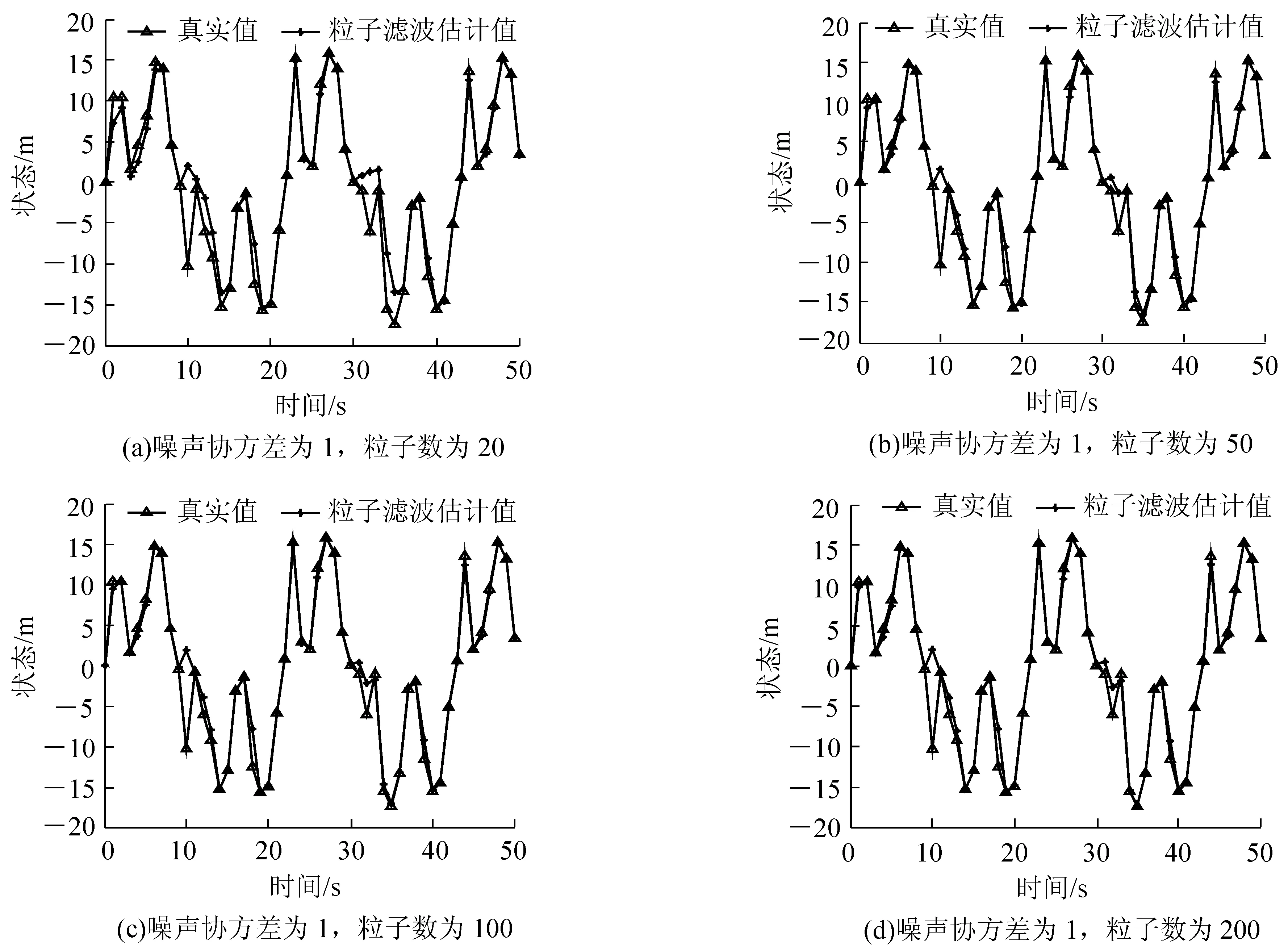
图3 噪声协方差为1，粒子数分别取20,50,100,200的仿真实验结果

图4是过程噪声与观测噪声协方差均为0.1，粒子数分别取值N=20、50、100、200时，用PF进行目标状态估计的实验结果。表2为不同噪声协方差情况下，粒子数分别取值N=20、50、100、200时的RMSE均值。

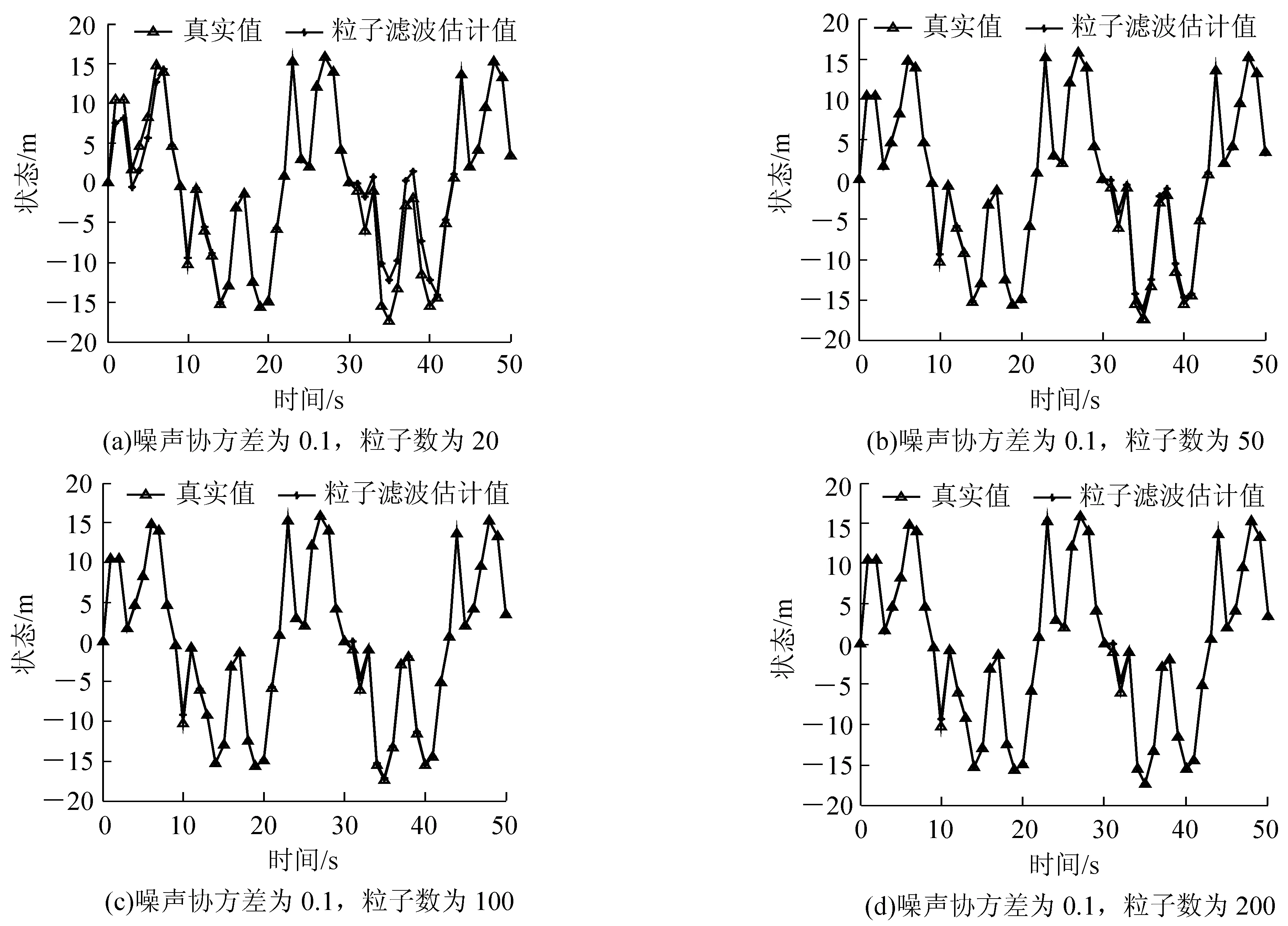
图4 噪声协方差为0.1，粒子数分别取20,50,100,200的仿真实验结果

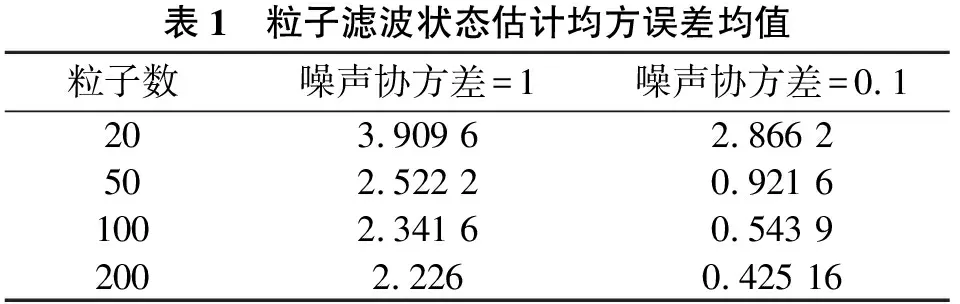
表1 粒子滤波状态估计均方误差均值粒子数噪声协方差=1噪声协方差=0.1203.909 62.866 2502.522 20.921 61002.341 60.543 92002.2260.425 16

由图3、图4均可以看出，噪声协方差值一定时，随着粒子数的增加，粒子滤波状态估计值与实际值的差值减小，粒子滤波状态估计值越能真实地反映系统真实状态。对比图3和图4以及由表1可知，降低噪声协方差的值，能够降低粒子滤波估计的误差，提高PF在目标跟踪中的跟踪精确度。

3 结论

通过仿真实验，对比了PF与EKF两种算法在强非线性条件下的运行目标跟踪的性能，并研究了噪声协方差与粒子数对PF跟踪算法的影响。实验结果表明：

(1)在强非线性条件下，PF能够准确的对目标的状态进行估计，相比于EKF有更高的精确度。

(2)随着噪声协方差的降低，粒子滤波的跟踪精度明显提高。

(3)在噪声协方差一定的条件下，粒子数的增加能够使粒子滤波的跟踪误差降低。

但是，粒子滤波跟踪算法也存在一些问题，比如：增大粒子数在降低运动目标跟踪误差的同时，会导致计算量迅速增加；在重采样环节会出现样本枯竭的问题等等，这些都会影响跟踪性能。对于前一问题，可以在保证跟踪误差较低的前提下，尽量减少粒子的数目；对于样本枯竭的问题，可以采用重采样-移动算法(Resampling-Move Algorithm)[8]等改进算法来解决，但改进算法有时会出现计算量大和收敛判断难等问题，所以这些问题都还需进一步研究。

参 考 文 献

[1]Haykin S Ed. Kalman Filtering and Neural Networks [M]. New York: John Wiley & Sons, 2001: 16-20.

[2]Barshalom Y, Li X R, Kirubarajan T. Estimation with Applications to Tracking and Navigation: Theory, Algorithms, and Software [M]. New York: John Wiley & Sons, 2001: 381-395.

[3]程水英，张剑云.粒子滤波评述[J]. 宇航学报, 2008, 29(4):1099-1111.

[4]Arulampalam M, Maskell S, Gordon N, Clapp T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Trans. on Signal Processing, 2002, 50(2): 174-188.

[5]Doucet A, Gordon N, Krishnamurthy V. Particle filters for state estimation of jump Markov linear systems[J]. IEEE Trans. on Signal Processing, 2001, 49(3): 613-624.

[6]胡士强，敬忠良.粒子滤波原理及其应用[M].北京:科学出版社,2010:22-24.

[7]韩磊，郭晓金，齐威，等. 改进的粒子滤波算法[J].电视技术,2012,36(7):16-23.

[8]Chen Zhe. Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond[R]. Hamilton: McMaster University, 2003.