基于成本迭代与需求迭代的四阶段交通模型双重反馈算法研究
,
(1. 广州市交通规划研究所,广东 广州 510030;2. 华中科技大学 土木工程与力学学院,湖北 武汉 430074)
0 引言
交通需求预测四阶段模型从提出至今已有半个世纪,在我国城市交通规划中应用也有20多年的历史,目前仍是工程领域最为流行的交通需求预测模型。但四阶段模型有其显著的弱点,四阶段模型的每一阶段依序进行,上一阶段的输出作为下一阶段的输入,在其序列步骤的不同阶段对于出行时间和交通拥挤效果的考虑并不一致,这必然会产生结果的不一致性。为克服这个缺点,学术界近年来提出并不断完善了交通需求预测组合模型。1993年TRB年会上Boyce提出了在四阶段模型中使用反馈的概念[1],通过多次迭代不断更新出行成本,将更新后的成本带入下一次循环,并重新计算出行分布和方式划分,直至模型收敛。Willumsen[2]在《Modelling Transport》中所给出的标准四阶段模型结构,也引入了迭代反馈的概念。Boyce et al[1, 3]对交通模型反馈算法进行了研究,利用CDTC(The Capital District Transportation Committee)交通模型研究了模型反馈迭代中不同权重对的模型收敛和计算时间的影响。南加州交通模型[4]也采用了基于成本迭代的反馈模型,并设置了最大迭代次数为5次。国内屈云超 等[5]对反馈四阶段法的计算过程进行了研究并将其运用到不同规模网络进行求解,着重研究权重系数、交通分布参数、出行总量对计算效率和计算结果的影响。Feng et al[6]对反馈迭代中的常数权重、MSA及改进MSA算法进行了研究。这些反馈算法的引入虽然解决了四阶段模型的不一致缺陷,但模型收敛的迭代次数仍比较多,耗时较长。 就如何改进模型结构,通过设计反馈算法并选择合适的交通分配方法,加快模型的收敛速度、减少模型运行时间做进一步研究。
1 基于成本迭代与需求迭代的双重反馈算法结构与模型
反馈算法在1993年被引入四阶段交通预测模型,一般而言是在出行分布、方式划分和交通分配3个模块之间进行反馈,即上一步的输出作为下一步的输入,循环迭代直至收敛或达到模型最大设定循环次数。BOYCE等人的研究成果对反馈算法做了进一步研究,在循环计算过程中引入了出行成本的迭代计算,即从第二次循环开始在出行分布和方式划分中使用的出行成本是考虑了上次一次迭代的出行成本和当前迭代的加权。出行成本迭代反馈算法在满足改进四阶段模型不一致性的前提下有效的提高了模型的计算效率,但对于目前城市交通系统日趋复杂,交通分区更加精细,特大城市的综合交通模型运行时间仍就难以接受,特别是在快速反应方面问题尤为突出,为此有必要对交通模型结构进一步优化,以寻求更高的模型效率。
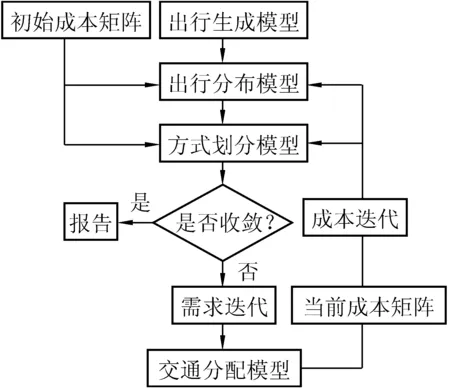
图1 成本+需求双重迭代模型结构
成本迭代与需求迭代双重反馈[7]的四阶段交通模型结构(以下简称“双重迭代模型”)是成本迭代反馈模型结构的改进情形。在该模型结构中首次循环使用自由流交通条件下的出行成本作为初始阻抗矩阵,从第二次循环开始,使用前一次迭代所得出行OD矩阵和当前迭代所得矩阵之和的1/2作为全有全无分配的输入矩阵,计算当前出行成本,并将当前出行成本与上次迭代出行成本之和的1/2作为新的出行成本矩阵,模型结构见图1。
模型中的成本主要应用于出行分布模型和方式划分模型。综合交通模型中的出行分布常用重力模型,其表达式如下
Tij=kijPiAjf(dij) (1)
式中,Tij为OD点对i,j之间的出行量;kij为OD点对i,j之间的社会修正系数;Pi为交通小区i的出行产生量;Aj为交通小区j的出行吸引量;f(dij)为OD点对i,j的出行阻抗,dij为OD点对i,j的出行成本,这里常用出行时间、出行矩阵、广义成本等,研究中使用出行时间。
对于方式划分,机动方式和非机动方式采用的模型不同。对于非机动方式而言常用转移曲线,变量为距离;而对机动方式则常用logit模型,变量为基于出行成本计算的各交通方式综合效用,数学模型如下
(2)
式中,pm交通方式m的出行比例;Um为交通方式m的效用函数;n为系统中的机动化交通方式总数。
对于非公交机动方式而言
U=αTTME+βCOST+const(3)
式中,TTME为出行时间;COST为之间的出行费用;const为交通方式的使用偏好;α,β为交通模型参数。对于公共交通方式而言
U=aIVT+bOVT+cNTR+dDWT+eTRTM+fCOST+const(4)
式中,IVT为车内时间;OVT为车外时间;NTR为换乘次数;DWT为等待时间;TRTM为换乘时间;COST为之间的出行费用;const为交通方式的使用偏好;a,b,c,d,e,f为交通模型参数。效用函数中所使用的各类时间和费用均为迭代成本。
模型结构中的成本迭代的数学模型如下
Miter=(Mcur+Mlast)/2 (5)
式中,Miter为本次循环出行分布与方式划分出行成本矩阵;Mcur为当前迭代计算所得出行成本矩阵;Mlast为上一次循环计算所得出行成本矩阵。
模型结构中的需求迭代的数学模型如下
Dm,iter=(Dm,cur+Dm,last)/2 (6)
式中,Dm,iter为本次循环交通方式m交通需求矩阵;Dm,cur为当前迭代交通方式m交通需求矩阵;Dm,last为上一次循环交通方式m交通需求矩阵。
2 案例分析
为了测试双重迭代模型的有效性,研究使用通用案例验证了模型可行性,并使用定制案例对其可靠性进行了进一步验证。通用案例选择了商业软件自带的案例,定制案例选择了广州、义乌、增城三个城市的综合交通模型。
2.1 通用案例
为了便于验证,算法测试以美国Citilabs公司开发的Cubetown[8]为测试平台。Cubetown模型包含25个交通小区,473个节点、1 145个路段,5条公交线路和5种交通模式(小汽车、小汽车合乘、小汽车接驳公交、步行接驳公交和步行)。以此为基础实现了基本迭代模型(M1)、成本迭代模型(M2)和双重迭代的模型(M3),并从模型的计算过程和结果两个方面对3种模型进行比较。从模型的效率来评价计算过程的合理性,从需求矩阵计算结果来分析模型的差异性。
2.1.1 效率分析
模型的效率更主要体现在计算时间消耗。减少计算时间消耗主要有2种途径,优化模型结构和算法设计,减少迭代次数;选择消耗时间较少的计算方法。这也是前述3种算法的设计的基本前提。
p=|Mcur-Mlast|/Mlast(7)
式中,p为变化比例;Mcur为当前矩阵;Mlast为上次迭代矩阵。

表1 模型收敛进程及需求矩阵变化 %
如表1和图2所示,从模型迭代次数和需求变化趋势来看,有以下特点:
(1)同时考虑需求迭代和成本迭代的模型结构收敛速度更快。
(2)仅考虑需求的更新迭代,需求矩阵变化虽然总体呈收敛趋势,但存在波动;同时考虑需求迭代和成本迭代的模型结构收敛趋势更加稳定,且不存在波动。
2.1.2 结果差异分析
算法的改进能够有效的提高模型的运算效率,但不同算法对应结果也存在一定的差异,为了分析成果的差异性,这里通过比较需求矩阵对应单元格数值来阐述。

图2 模型收敛变化

表2 不同算法小汽车出行矩阵单元格相关系数
从表2和图3来看,不同模型的计算结果有以下特点:
(1)在满足需求总量差值在1%以内作为约束条件的前提下,各算法计算结果总体差异较小,相关系数都在0.98以上。
(2)双重迭代算法与成本迭代算法的结果更为接近。
总体来说,在模型约束条件达到一定程度,不同模型结构计算所得结果差异较小。
2.2 定制案例
由于模型采用的是启发式算法,为了进一步验证算法的有效性研究采用了广州综合交通模型、增城综合交通模型、义乌交通模型进行测试,并比较了迭代次数与成本迭代(M2)和双重迭代(M3)的相关系数指标,结果见表3。

表3 其它案例测试结果比较
表3的结果表明研究提出的成本迭代+需求迭代的双重迭代四阶段模型结构能够适用于不同规模的交通网络模型,在保证模型计算结果的前提下,减少四阶段模型循环迭代次数(28%~40%),有效提高模型的运行效率。

图3 不同算法小汽车出行矩阵单元格相关关系
3 结论
本文提出了成本迭代+需求迭代的双重迭代四阶段模型结构,并通过案例与基本四阶段模型结构和成本迭代四阶段模型结构进行了比较。结果表明,与成本迭代算法相比,本文提出的“需求迭代”+“成本迭代”的双重迭代反馈算法在保证计算结果变化不大的前提下,能够减少模型循环迭代次数(28%~40%),减少系统运行时间,显著提高四阶段模型的效率且收敛过程更加稳定。此外,案例分析结果表明,双重迭代四阶段模型结构在不同规格的交通网络均有效。
参 考 文 献
[1]Travel demand modeling and network assignment models[R]. WASHINGTON, D.C.:Transportation Research Board/national Research Council,1994.
[2]De Dios Ortúzar J, Willumsen L G. Modelling Transport[M]. 4th ed. Hoboken, New Jersey:J. Wiley, 2010.
[3]Boyce D, Neill C R O, Scherr W. Solving the sequential travel forecasting procedure with feedback[J]. Transportation Research Record,2008, 2077: 129-135.
[4]Scag regional travel demand model and 2008 model validation[R]. LSA Associates, Inc., 2012.
[5]屈云超,徐猛.求解交通出行预测的反馈四阶段法研究[J]. 中国科技论文在线,2008,3(10): 725-730.
[6]Feng X, Mao B, Sun Q. Comparative evaluations on feedback solutions to the feedback process of a new Model for urban transport study[J]. International Journal of Urban Sciences,2010,14(2): 164-175.
[7]陈先龙.基于反馈算法的四阶段交通模型研究[D]. 武汉: 华中科技大学, 2013.
[8]Citilabs. Discover Cube 5.0 Tutorial[M]. Lafayette, California:Citilabs,2009.

