基于仿真的铁路车轮不圆度安全限值研究

, ,

(1.石家庄铁道大学 交通运输学院,河北 石家庄 050043；2.石家庄铁道大学 大型结构健康诊断与控制研究所,河北 石家庄 050043)

0 引言

安全和高速是高速铁路建设首先要考虑的核心问题，各种轮轨不平顺现象将引起车辆轨道系统一系列动力响应的变化，对行车稳定性和安全性以及车辆轨道系统各个部件使用寿命有很大影响[1-2]。特别是在高速行车条件下，车轮不圆顺现象如不及时发现将会继续发展，不但严重影响乘车舒适度而且危及行车安全。有关车轮非圆化的试验检测和数值模拟一直是国内外学者研究的热点问题。Nielsen J. C. O. et al[3]就轮轨表面不规则磨耗及其对车辆轨道系统动力学行为的影响进行了评述，包括Ahlbeck和Hadden分析的北美走廊高速线上车轮非圆化所引起的冲击荷载，Zacher和Pallgen研究的德国ICE高速列车车轮周期性不圆顺问题，以及Muller等在Gotthard专线进行的相关试验研究。Johanssonp A. et al[4]通过数值模拟、现场试验和跟踪检测，对车轮非圆化的产生原因、动力学效应以及车轮型面的发展趋势进行了分析，提出了波长固定机理。翟婉明[5]、郑伟生[6]对车轮踏面局部不圆顺如车轮扁疤、擦伤剥离问题进行了研究。张雪珊 等[7]对车轮椭圆问题对车辆横向稳定性的影响进行了理论研究。陈光雄 等[8]对车轮多边形磨耗机理进行了有限元分析，并提出了相应的控制对策。我国高速铁路发展较晚，如何确定高速铁路车轮不圆顺量化管理标准，确保乘车舒适度与行车安全，还有待深入研究。建立考虑车轮非圆化状态的车辆轨道空间耦合动力学仿真模型，研究高速情形下车轮不圆顺的波长、幅值、类型等因素与轮轨动力学特性之间的关系，探讨车轮不圆度控制问题。该研究可为基于轮轨作用力检测的车轮不圆顺状态识别提供理论指导。

1 仿真模型

常见的铁路车辆车轮不圆顺现象包括局部非圆化和全周非圆化两大类，前者如扁疤、剥离、长波长局部非圆化等，主要指车轮踏面局部出现的车轮径向偏差；后者主要指车轮多边形现象，即车轮半径相对整个圆周方向出现周期性的不圆度偏差。为了研究高速车轮非圆化问题对轮轨动力学行为的影响，采用翟婉明教授提出的车辆轨道垂横向耦合动力学理论[5]，基于ADAMS/Rail动力学仿真平台，建立车辆/轨道空间耦合系统动力学仿真模型。

图1 车辆系统动力学仿真模型

车辆系统以我国具有二系悬挂的CRH2型高速动车组为建模对象，采用整车模型，由1 个车体、2 个构架、4 位轮对和8个轴箱、一系悬挂和二系悬挂组成的多刚体系统(如图1所示)。车轮踏面采用LMa磨耗型踏面，车体、转向架和轮对三大构件之间的连接简化为弹簧和阻尼单元，设定了弹簧单元纵向和横向的上下限。转向架为两轴无摇枕式H型构架之转向架，一系悬挂装置采用转臂式轴箱定位方式，安装垂向减振器和轴箱弹簧；二系悬挂安装有抗侧滚扭杆、空气弹簧系统、二系横向减振器、二系垂向减振器、横向止挡、抗蛇行减振器等。空气弹簧采用Krettek空气弹簧模型进行简化。非线性比较明显的单元都考虑了非线性特性，如弹簧和减振器的刚度和阻尼都考虑了非线性特性，横向止挡的刚度随挠度的增加逐渐提高。车体、构架、轮对均考虑纵向、横移、浮沉、测滚、点头、摇头6 个自由度，每辆车共42 个自由度。

轨道系统采用钢轨-轨枕-道床-路基弹簧阻尼简化振动模型，钢轨视为连续弹性离散点支承基础上的无限长Euler梁，并考虑钢轨的垂向、横向和扭转振动。轨枕视为刚性体，轨枕与钢轨之间以及轨枕与路基之间在垂向和横向均采用线性弹簧和粘性阻尼连接，并考虑其垂向、横向振动及刚体转动。道床被离散为刚性质量块，道床块之间由剪切阻尼元和剪切刚度件相连，道床和路基之间由阻尼元件和线性弹簧连接，并且只考虑垂向振动。轮轨接触力计算基于Hertz非线性单向约束弹簧计算模型和Shen-Hedrick-Elkins非线性理论求解。

轮轨瞬态接触几何关系计算考虑了车轮瞬时滚动圆的不圆度偏差，如图2所示，车轮不圆度误差以增量Δr的方式表示为车轮初始名义接触半径滚动角φ的函数，给出了一个描述车轮非圆化的计算方法

(1)

式中，R0为车轮名义滚动圆半径，车轮滚动圆为距离轮缘70 mm位置处;φ(t)为t时刻车轮初始名义接触半径与水平轴的夹角，在0～2π之间;ω为车轮滚动角速度;Δt为积分时间步长。通过调整每一时间步的车轮初始名义接触半径Rw来计算轮轨接触几何参数。仿真计算过程中，在考虑同轴左右车轮非圆化状态的基础上，求解轮轨接触几何关系及轮轨力特性。

2 车轮不圆度安全限值的研究

2.1 车轮谐波不圆顺安全限值

车轮谐波不圆顺是指在车轮踏面局部形成的简谐波形式不平顺，如图3所示，有单次谐波不圆顺、双次谐波不圆顺、连续谐波不圆顺等几种类型。车轮不圆度Δr(φ)的数学描述如下

(2)

式中，a为不圆顺波深；L为不圆顺波长；n为谐波次数，如单次谐波不圆顺n=1，双次谐波不圆顺n=2。

根据现场试验调查，一些典型的车轮谐波不圆顺，波长范围L为400～800 mm，波深a为0.5～2.0 mm[3]。采用建立的动力学仿真模型，以单次谐波不圆顺为例，对车轮谐波不圆顺激扰作用下轮轨动力作用响应最大值与行车速度、不圆顺波深和不圆顺波长的关系进行了仿真计算。当车速为300 km/h，车轮单次谐波不圆顺波深为0.5 mm，车轮不圆顺波长与轮轨动力作用响应最大值的关系曲线如图4(a)所示。当不圆顺波长为500 mm，轮轨动力作用响应最大值与不圆顺波深和车速的关系如图4(b)所示。由仿真结果可以看出，车轮谐波不圆顺引起的轮轨冲击作用，随其波长的减小而迅速增大，随不圆顺波深和车速的增加而显著增大，且波深比速度的影响更为显著。如表1所示，在相同速度(v=300 km/h)下，波深由1 mm增至2 mm，最大轮轨力增大了76.1%；相同波深(a=1 mm)下，速度从250 km/h提高到350 km/h，最大轮轨力增加了27.0%。由此可见，需要对车轮踏面局部谐波不圆顺的不圆度进行限制，以保证行车安全性和舒适性。根据仿真计算，采用轮轨动力作用响应峰值是衡量车轮不圆顺所引起的轮轨动力学效应强弱的最直观指标，根据GB 5599—85,将轮轨作用力最大许用值定为[Pmax]=250 kN，计算结果表明：车速为250 km/h、300 km/h和350 km/h时车轮不圆度的安全限值分别约为0.95 mm、0.8 mm和0.7 mm，如图4(b)所示。

图2 车轮不圆顺示意图 图3 车轮谐波不圆顺示意图

图4 车轮谐波不圆顺的动力学效应

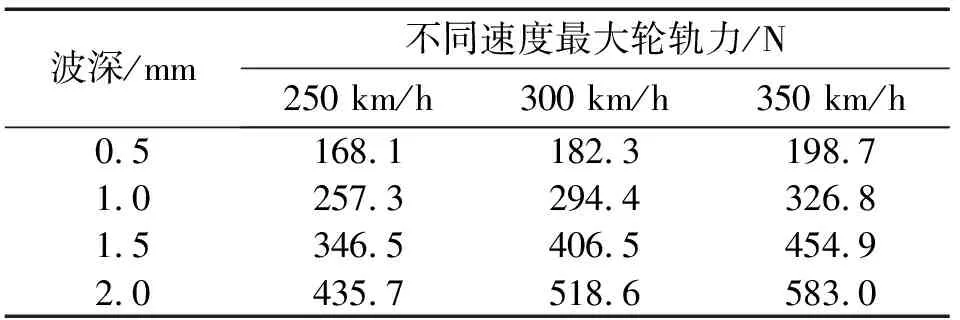
表1 车轮局部谐波不圆顺产生的轮轨动力响应最大值

2.2 车轮多边形磨耗安全限值

车轮多边形磨耗是车轮踏面不圆顺的一种特殊表现形式，在车轮表面呈现出一种周期性不圆顺，其波数(或称边数)以θ表示，磨耗幅度为mm量级左右，根据文献[4]，发现车轮多边形波磨的波长分布在0.1 m到整个滚动圆周长之间，波数在1～20之间。车轮多边形磨耗的波长λθ和波数θ符合“波长固定机理”，Δr(φ)可表示为

Δr=aθsin(θφ) (3)

式中，aθ为不圆顺波深;θ=1,2,3,…。

一阶车轮多边形化即车轮偏心(θ=1)，相当于一类连续周期性激扰源，它以车轮离心激振力作为输入，其所产生的轮轨系统附加动作用力与车速和偏心距 的关系如图5所示。由图5可知，轮轨作用力随车速和偏心距的增加而增强，当偏心距为1.5 mm，车速增加到350 km/h时，车轮与钢轨还会出现瞬间脱离的现象，因此，高速机车车辆的轮对应进行严格的动平衡试验。

图5 冲击荷载与车速和偏心距的关系

图6 椭圆车轮激励下轮轨动力作用响应

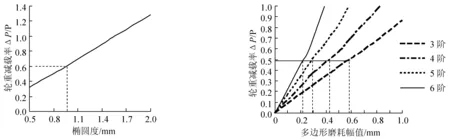
图7 车轮椭圆度安全限值 图8 车轮多边形磨耗幅值安全限值

对于三阶以上的车轮多边形化，同椭圆车轮的激扰性质相同，均是引起车辆轨道系统产生周期性的强迫振动。引起车辆侧滚，导致轮重减载率增大。仿真计算了车速为300 km/h，3阶～6阶车轮多边形化激扰作用下车辆轨道系统的动力学效应，其中轮重减载率随车轮多边形磨耗幅值变化的关系曲线如图8所示，根据GB 5599—85,轮重减载率安全限值为0.6。由图8可知，当车速在250 km/h至300 km/h之间时，车轮“三角形化”(即3阶车轮多边形化)的不圆度安全限值为0.25 mm，车轮“四边形化”(即4阶车轮多边形化)的不圆度安全限值为0.35 mm，车轮“五边形化”(即5阶车轮多边形化)的不圆度安全限值为0.5 mm，车轮“六边形化”(即6阶车轮多边形化)的不圆度安全限值为0.7 mm。对于6阶以上的车轮多边形化，根据轮轨动力作用响应峰值与车轮多边形磨耗幅值关系的仿真计算分析，其多边形化的不圆度幅值不应超过0.2 mm。

3 结束语

根据分析可以看出，车轮滚动圆非圆化会引发车辆轨道系统强烈的冲击振动，而且在高速情形下的危害远大于在常规速度时的影响，即使是幅值很小的高阶车轮多边形非圆化也有可能出现轮轨脱离进而导致强烈的冲击振动，是行车安全方面的重大隐患。基于不圆顺车轮激扰下的轮轨间动力作用与列车运行速度及车轮不圆顺状态的规律，结合仿真计算得出的各种车轮的不圆度安全限值与轮轨动力作用响应峰值的关系，可以通过轮轨作用力的监测识别车轮失圆的类型以及判断车轮不圆度与行车安全的关系。

因此，实时监测车轮多边形化所引起的轮轨力异常情况，对防止轮轨动力作用的恶化、保护轮轨免遭损害、以及预防车轮多边形化的发展具有积极意义。

参 考 文 献

[1]张新,李向国,王海云,等. 轨距不平顺激励下高速列车动力响应研究[J]. 石家庄铁道大学学报:自然科学版,2011,24(1):69-72.

[2]Nielsen J C O, Lunden R, Johansson A, et al. Train-track interaction and mechanisms of irregular wear on wheel and rail surfaces[J].Vehicle System Dynamics,2003, 40(1/3):3-54.

[3]Nielsen J C O, Johansson A. Out-of-round railway wheels-a literature survey[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2000, 214:79-91.

[4]Johansson A. Out-of-round railway wheels-A study of wheel polygonalization through simulation of three dimensional wheel-rail interaction and wear[J].Vehicle System Dynamics, 2005, 43(8):539-559.

[5]翟婉明.车辆-轨道耦合动力学[M].2版.北京： 中国铁道出版社, 2002.

[6]郑伟生.关于车轮擦伤剥离的若干问题与对策[J]. 铁道车辆, 2001, 39(2)：19-23.

[7]张雪珊,肖新标, 金学松. 高速车轮椭圆化对车辆系统行为的影响[J]. 机械工程学报, 2010,46(16):67-73.

[8]陈光雄, 金学松, 邬平波, 等. 车轮多边形磨耗机理的有限元研究[J]. 铁道学报, 2013,33(1):14-18.