基于PLC的流量累积误差及解决方法

华优基

(江西省萍乡钢铁公司，萍乡 337019)

0　引言

在工业计量中，流量累积就是将瞬时流量乘以时间而得到一段时间内的总流量，为实现由PLC对瞬时流量的动态累积，通常的方法是利用PLC的定时中断组织块OB35，对单位小间隔时间内的瞬时流量乘以单位间隔时间，得到单位小间隔时间内的流量，再把这些小流量累加起来，就得到了累积流量。计量所需要的通常就是累积量，对于一个由PLC做运算单元的流量测量系统来说，累积量的误差包括流量计本身误差、D/A误差、A/D误差和PLC流量累积误差，这其中PLC流量累积误差当属计量部门控制的误差，这也是本文阐述的主要内容。

1　矩形积分法和梯形积分法的累积误差

我们通常所做的流量累积程序，其实就是基于矩形积分的原理，如图1，把单位小间隔时间内的瞬时流量乘以单位间隔时间，得到单位小间隔时间内的流量，再把这些小流量累加起来，就得到了累积流量。图1的阴影部分是用矩形积分法做流量累积的误差。

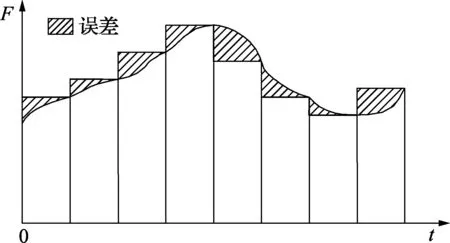
图1　矩形积分法误差示意图

梯形积分法就是以单位间隔时间的起始时刻和终了时刻的瞬时流量采样值作为梯形面积运算的上、下底,以单位间隔时间的梯形高度计算梯形的面积，得出累积流量，如图2。在用STEP7编程时，我们仍然采用OB35中断，只是上、下底分别为上次和本次采样的瞬时流量。

图2　梯形积分法误差示意图

从图1和图2的阴影部分可直观地看到，梯形积分法的累积误差明显小于矩形积分法；从文献[2]给出的比较结果看，梯形积分法的累积误差约为矩形积分法的一半。因此在做流量累积运算时，宜采用梯形积分法，而梯形积分法的运算并不复杂。

2　补偿浮点数的舍入误差

2.1　舍入误差的产生及实验

有限位数的二进制数不能精确表示所有十进制数值，当PLC系统不能精确表示一个数时，浮点运算和输入结果会被舍入到最邻近的表示值，产生舍入误差。浮点加法运算在对阶时,尾数要向右移位,被右移的尾数的低位部分会被丢掉,这种处理过程就会产生误差,这也是一种舍入误差，最终使运算结果不准确。

在PLC做流量累积时，需要不断地做累加运算，由于浮点数运算的舍入误差累计的结果，随着累加次数的增加最终结果的误差会相当大，我们用STEP7编程累积运算结果见表1。

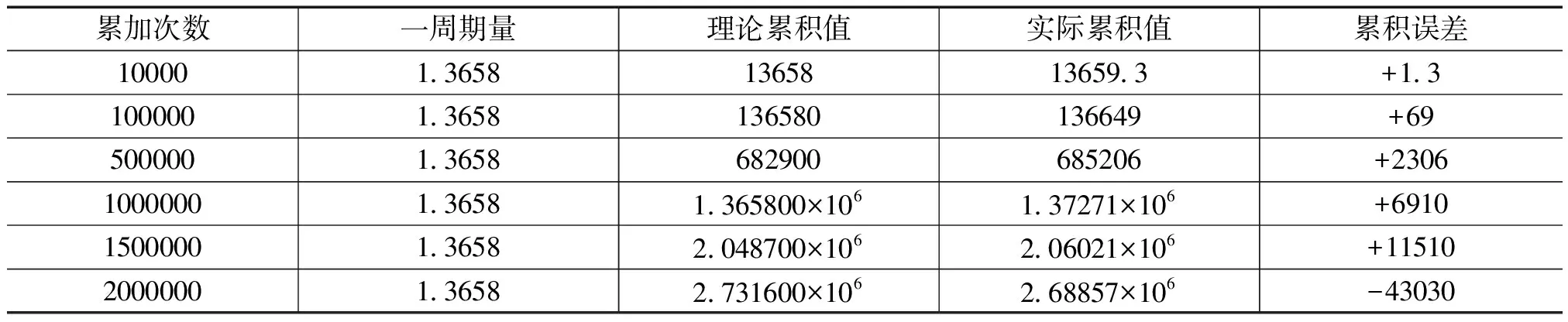
表1　浮点数累积误差测试

2.2　舍入误差的补偿及实验

由此可见，流量累积的误差必须预以补偿，其算法如下：

当前周期量=一周期量+以前计算误差

当前累积量=当前周期量+原累积量

当前计算误差=原累积量-当前累积量+当前周期量

算法中，误差主要出现在第二步，当前周期量与原累积量的累加，第三步当前计算误差，看似此式会等于零，但它恰恰得出了第二步的计算误差，得到的“当前计算误差”将作为下一周期的“以前计算误差”。通过用STEP7编程，实现上述补偿运算，得到的流量累积结果如表2。

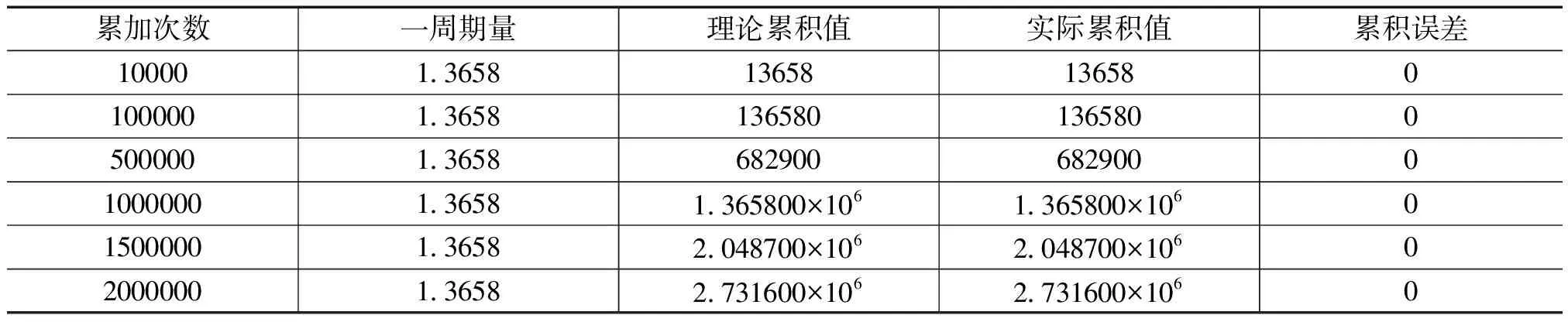
表2　经误差补偿的浮点数累积误差测试

表2中我们选择的累加次数都是后面有多个零，而一周期量的小数点后的位数有限，因此看到的累积误差均为零。但如果累加次数的后面几位不是零，实验表明累积误差就不是零了，这是由于STEP7浮点数只能精确到6位小数所致。实验还表明，当累积值达到108级时，对于周期量1.3658这样一个小数将被累积量这个大数“吃掉”，而这种补偿算法无法解决这样的问题。

3　避免“大数吃小数”

3.1　STEP7的浮点数表示法

STEP7中的浮点数符合IEEE754标准的单精度浮点数规范的基本格式，由符号位S、指数e和尾数m三部分组成，见图3。

图3　STEP7浮点数格式

3.2　“大数吃小数”的成因

浮点数的加、减运算，只有使两浮点数的指数值部分相同，才能将相同的指数值作为公因数提出来，然后进行尾数的加减运算。为此，必须对参与加减运算的两个浮点数进行对阶，使指数归齐。

当两个浮点数的数量级别相差太大时，例如7865932.3与0.426相加，首先进行对阶，结果7865932.3=7.865932e+6,0.426=0.000000426e+6=0.000000e+6。

由于STEP7中浮点数最多只能精确到6位小数，对阶的结果使小的那个数变成了0，最终体现为两数不累加，这就是通常所说的“大数吃小数”。

用PLC做流量累积，随着累积量的不断增大，而一周期量相对是个很小的数(特别是采样周期短时)，小数的有效位数丢失，累积的精度就越来越低，而后一周期量小到被对阶为零，这就形成“大数吃小数”，有瞬时量而流量不累积，失去流量累积功能。

3.3　“大数吃小数”的解决

解决“大数吃小数”的办法，就是实行多级累加，低一级的加法对一周期量做累加，流量累加到一定数值后，例如累计值超过10000，就把累积值减去10000，然后向高一级加法器进位。低一级的累加保证被加两数的数量级别相差不会太大，对阶时不会将一周期量变成零，选择合适的进位值还可以避免小数的有效位数丢失，保证累积流量有较好累积精度。

4　具有较高精度的流量累积程序

综合上述三项提高流量累积精度的措施，我们得到一个具有较高精度的流量累积程序，它采用梯形积分法，以本次采样和上次采样的瞬时流量作为梯形的上下底计算被测流量的一周期量；然后按浮点数累加的补偿算法计算并补偿上次累加的误差，可以使流量累积误差控制在一次累加误差的范围内，大大减少了舍入误差的影响；我们还设置了两级加法运算，浮点数累加的补偿算法属于低一级加法运算，当累积结果超过10000时向高一级加法运算进位，高一级加法运算采用双整数加法，避免了“大数吃小数”的发生。

综上所述，以STEP7编写的置于OB35的流量累积程序如下：

L#a；本次瞬时流量采样值m3/h

L#a1；上次瞬时流量采样值m3/h

+R

L7200.0

/R；一周期量

L#L；以前计算误差

+R

T#m；当前周期量

L#C1；原累积量

+R

T#C:当前累积量

L#C1

L#C

-R

L#m

+R

TL；当前计算误差

L#C

L10000.0

>=R;累积量大于10000，则高一级加法器加一。

JNB_003

L#C

L10000.0

-R

T#C

L#H;高一级累加量

LL#1

+D

T#H

_003A#Z；清零

JNB_001

LL#0

T#H

_001L#a

T#a1

5　结束语

本文对PLC流量累积的误差问题从梯形积分、浮点加法的舍入误差和大数吃小数问题三方面进行论述，用西门子STEP7编写相应程序并进行各项实验，由此形成了具有实用价值的高精度流量累积程序，较全面地解决了目前PLC流量累积误差的主要问题，对确保工业物料流量计量的准确性，实现高精度流量累积，提升企业计量水平具有重要意义。

[1]夏冰.PLC在流量显示和累积计量上的应用[J].计量技术，2009(10):68-70

[2]郑立飞，解小莉，王洁.关于定积分近似计算中矩形法的误差估计[J].高等数学研究,2011,14(1):5-6

[3]张泽宏，孟涛，胡鹤鸣.超声流量计积分方法检验软件的设计[J].计量技术，2013(1):10-13

[4]吴幼庸.电子皮带秤累计量计量数学模型[J].计量技术，2011(1):26-29

[5]廖常初.S7-300/400PLC应用技术[M].北京：机械工业出版社，2012

[6]张建勇，王克.测量氧气的节流装置在设计上的分析和探讨[J].计量技术，2013(6):34-36