大口径超声流量计延时误差的安装前校准*

曹　鹏　孟　涛　张　亮　胡鹤鸣　徐春荣

(1.河北大学，保定 071002；2.中国计量科学研究院，北京100029；3.南京申瑞电气系统控制有限公司，南京 210000)

0　引言

由时差法超声流量计原理可知，流量测量相关参数有管道直径D、声道长度L、声速C、声道角φ和时间差Δt。为减少各项参数给流量计算所带来的误差，需要保证D、L、C、φ、Δt每一项测量的准确性。因此，本论文针对超声流量计其中一项参数——传播时间进行研究，超声平均传播时间是参与流速计算的关键参数之一，其测量的准确性会直接影响流量测量结果的可靠性。流量计算的传播时间是指超声波由换能器的发射面发出穿过被测介质到换能器接收面接收为止，即超声通过两探头间固定声道长度的传播时间。而流量计实测时间还包括了电信号的线缆延时、软硬件电路运算延时以及超声波穿过探头前端的匹配层、保护层所产生的延时等[1]，这些延时会直接影响传播时间的计算。

由系统自身原因所产生的计时误差统称为延时误差，延时误差对流量测量准确度的相对影响与流量计口径相关，口径越小影响越显著。对大口径超声流量计来讲，通常认为延时误差量级相对较小，大部分流量计厂家采用相对粗放的理论计算方式进行修正。但实际使用中，由于线缆较长，软硬件电路运算延时等原因，延时可达几个微秒，在这种情况，计算本身误差较大，其结果必然不准确，会对流量测量产生明显影响。

在JJF 1358—2012《非实流法校准DN1000～DN15000液体超声流量计》[2]中已对延时误差的校准给出了实验方法。由于实验条件所限，三峡电站已安装的流量计只能采用现场声速校准的方法对流量计计时系统进行检查，但声速测量容易受系统、装配条件、环境等因素的影响[3]，检查所带来的不确定度较大，检查结果并不适用于对流量计的修正。在本实验项目中，恰逢溪洛渡电站流量计到货且准备安装，经流量计厂家协调配合，在实验室完成了溪洛渡9#机组流量计的延时校准。

1　延时误差校准装置及实验

1.1　延时装置基本原理

该延时装置基于水温恒定的静水中超声波声速基本保持一致，声波信号在整个系统中往返延时Δt相同的特点，把参与计算的时间参数作为变量，如图1，通过调节声道长度的变化，精确测量声波实际传播时间，得到系统带来的延时误差Δt。

图1　超声传播时间校准装置原理图

如图1所示，利用两个精确测量的传播距离L1和L2，分别测量得到声波在传播距离L1和L2上的传播时间t1和t2，而实际水域中的传播时间为t1+Δt和t2+Δt，因此，根据声速在相同环境和介质中的一致性得到：

(1)

若无法完全保证一长一短两次测量过程中温度完全一致，而温度的变化会对声速带来影响，因此，上式可进一步改为：

(2)

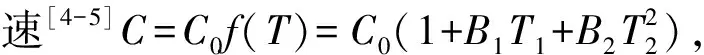
1.水槽；2.注水口；3.排水口；4.滑轨；5、6.被测流量计探头；7.流量计主机；8.滑动探头夹装机构；9.固定探头夹装机构；10.石英棒；11.温度传感器；12.温度采集器

1.2　延时校准装置

探头间距的选择及控制精度是装置设计中的关键因素，装置的测量精度与超声探头在装置上定位精度密切相关，如图2所示，装置对探头间距离控制机构进行了精心设计，使探头间距离控制精度可以达到0.05mm以内，大大提高了探头间距离测量不确定度水平。

本装置其它误差来源对延时误差的贡献量较小，通过温度修正可以降低由于两次测量中温度变化引起的误差，温度测量采用准确度优于0.1℃的铂电阻。

2　实验数据分析及处理

2.1　18声道超声流量计系统延时校准

该项实验选择了即将安装的溪洛渡电站9#机组流量计。流量计为18声道，按照Gauss-Jacobi方式[6]布置探头(如图3)， 每个换能器的电缆长度

图3　18声道超声流量计声道布置示意图

为90m，在实验开始前，流量计厂家已按照其技术规范计算得到其延时误差为8.4μs，并已置入流量计算机中。

将18对探头依次分别安装在延时校准装置上，延时校准装置共配备了3种长度的标准距，分别为1000mm、300mm及200mm，采用不同组合对每对探头测试3次，取平均值，实验结果的处理方法如式(2)所示。

声道长度按照18声道流量计安装管径为10m(设计值)，依据Gauss-Jacobi探头布置方法计算得到；理论传输时间是在静水状态下，水温为20℃，水中声速为1480m/s估算得到。如图4所示，黑色线表示理论传输时间，符合换能器探头布线方式，白色柱表示各声道平均延时的情况。各声道中最长声道长度为11.034m，理论传输时间为7455.4μs；最小为3.410m，理论传输时间2304.1μs；各声道平均延时误差绝对值最大为3.3468μs，绝对值最小为3.0430μs，平均值为3.2204μs。引入的流速测量误差最大值为-0.15%，出现在Path9；最小值为-0.04%，出现在Path4、Path5和Path14。

图4　各声道实测平均延时

经延时校准装置标定后，在满足设定的声道长度下，每一声道实测平均延时基本保持在-3～-3.35μs之间，由此对流量计流速测量造成的误差在0.1%左右，其贡献量是比较大的。相对于系统设定延时8.4μs偏差约38.1%，修正后，系统延时的设定值延时为5.0532～5.3570μs。

2.2　流量计安装现场实测数据分析

在相同的测量条件下，经过延时误差校准，各声道声速测量结果将趋于一致，在溪洛渡电站9#机组流量计安装好之后，调取现场声速测量数据对校准结果进行检验，数据如图5所示。

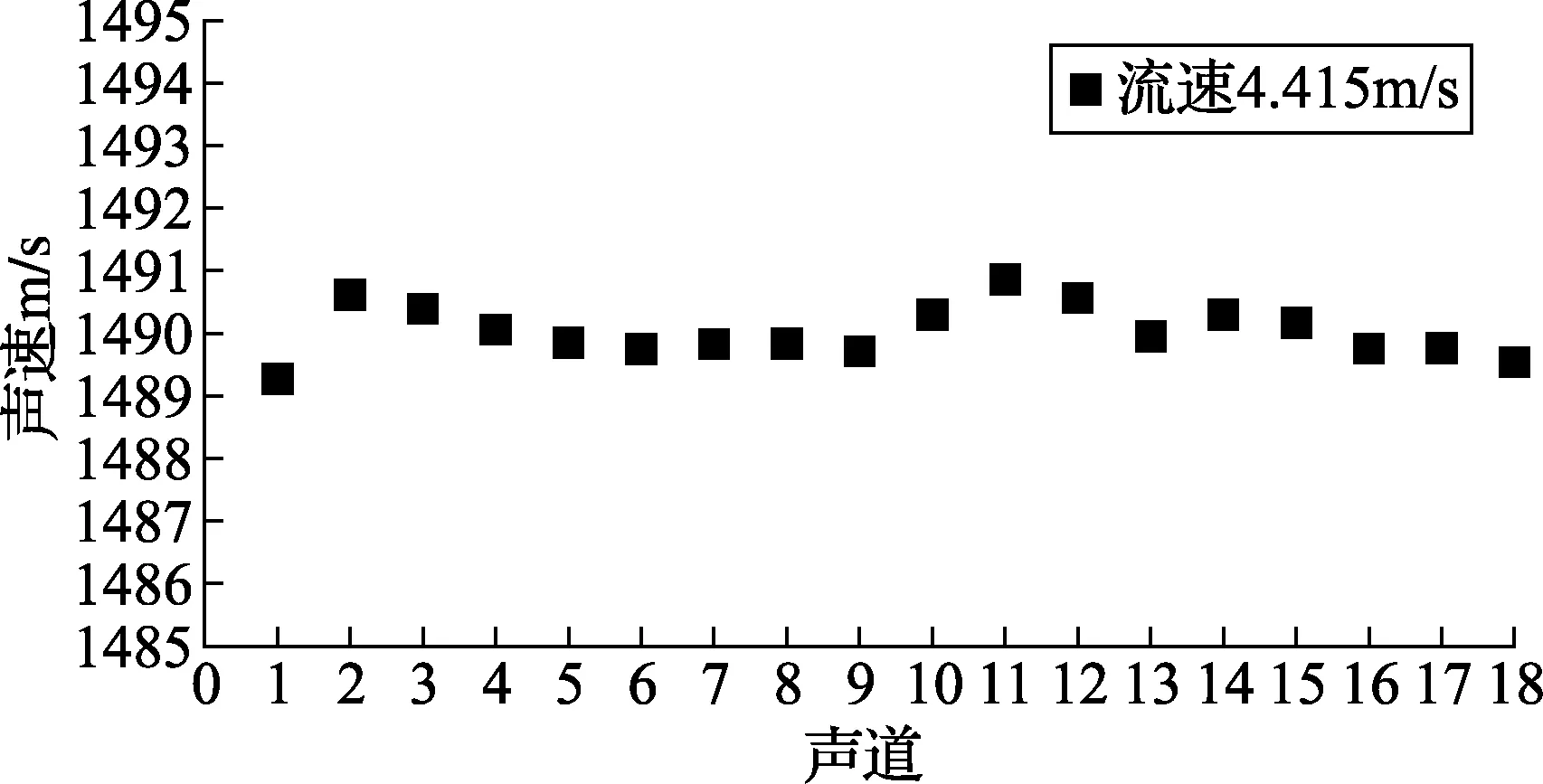
图5　9#机组流量计平均声速

如图5，各声道声速测量的一致性整体上是非常好的，根据贝塞尔公式计算得到，18条声道的一致性为99.97%。流速为4.415m/s状态下，各声道声速的标准偏差大约为0.089m/s，各声道声速基本保持在稳定的状态，验证了静水状态延时校准装置修正系统延时的有效性。

3　结论

由图4可以看到，每条声道的平均延时比较接近，说明每条声道的一致性较好；各声道平均延时平均值约为-3.2μs，其含义可以理解为流量计算机置入的8.4μs偏大了约3.2μs。用平均延时除以理论传输时间即可得到由于延时修正不准确引入单条声道流速测量的误差，该误差在管道边壁声道最大，达到0.15%，而管道中心声道误差约为0.05%；由于在计算流量时，各声道的权重系数不同，因此，在评估延时对流量测量影响时，也采用加权平均的方法，计算得到延时引入流量的误差约为0.06%，而为流量计重新置入延时修正值(校准后设定值)后，延时误差可被基本消除。由溪洛渡电站9#机组流量计实测数据分析得到，现场18声道超声流量计声速相对一致性较好，表明装置的系统延时得到了有效修正，满足大口径超声流量计的使用需求。

4　结束语

对于该流量计，若不对延时进行修正(流量计设置修正值为0)，延时误差将会引起流量超过0.1%的误差。由此可见，即便对于超大口径流量计，延时误差的有效消除也能明显提高流量计的准确度，而相比原有的延时计算方法，项目中使用的实验设备及方法亦不复杂。从上述的实验结果中进一步分析得到：若已知被测流量计各声道延时一致性较好，如换能器为同一批号、电缆材质长度相同、共用一套时间测量系统等，实验可简化为仅测几个典型声道延时即可，用典型声道的延时数据为每条声道进行修正，其引入的误差是完全可以接受的，实验量则得到进一步减少，增加了实验的可操作性。

本实验中反映出的另一个问题，需要流量计的用户和生产企业共同思考。近年来，流量计现场校准的需求越来越多，但实际情况是在流量计安装、投入使用后，很多校准项目开展非常困难，只能将校准变为检查，而有些项目则根本无法进行；若用户能将校准需求提前到流量计的安装前，甚至是设计阶段，并及时与相关的计量技术部门沟通，使得部分校准项目可以在实验室完成，再通过与现场检查相结合(本实验中溪洛渡电站9#机组流量计校准作为例证)，在实验室延时校准后，可在现场检查流量计各声道声速测量情况，对实验室校准结果进行核查，这将是解决流量计现场校准困难的一条有效路径。另一方面，对于流量计生产企业，也应切实加强产品的出厂检测以及现场安装后的调试，将操作方法规范到JJF 1358—2012《非实流法校准DN1000～DN15000液体超声流量计》上，这将为后续的现场校准及周期校准奠定良好基础。

[1]晁智强,盛锋,韩寿松.时差法超声波流量计误差分析与研究[J].液压与气动,2009(6):64-67

[2]JJF 1358—2012非实流法校准DN1000～DN15000液体超声流量计校准规范[S]

[3]孟涛,胡鹤鸣,王池,等.三峡电站流量计准确度评估实验模型设计[J].计量技术,2009(11):32-35

[4]V A Belogol’skii, S S Sekoyan, L M Samorukova, et al.Pressure dependence of the sound velocity in distilled water[J].Measurement Techniques, 1999, 42(4)：406-413

[5]张亮,徐益挺,孟涛,等.超声流量计系统延时检定方法研究[J].计量技术,2013(3):45-47

[6]胡鹤鸣,王池,孟涛.多声路超声流量计积分方法及其准确度分析[J].仪器仪表学报,2010(6):1218-1223