简支组合梁长期变形下混凝土收缩模式研究

李 达，牟在根

(1. 北京科技大学土木与环境工程学院，北京 100083； 2. 太原理工大学阳泉学院，山西阳泉 045000)

流态混凝土在固化过程中因失水、化学反应及温度降低等因素引起的体积缩小现象，称为混凝土的收缩。在长期荷载作用下，钢-混凝土组合梁会因翼缘混凝土的收缩而产生附加挠度变形。本文在前人研究的基础上，分析了不同收缩模式下附加变形的发展趋势和特点，建立了基于混凝土收缩的组合梁附加挠度计算模式。

1 常用混凝土收缩计算模式简述

影响混凝土收缩变形的主要因素有：水泥的品种和用量；水灰比；骨料的性质、粒径和含量；养护条件；使用期的环境条件；构件的形状和尺寸(体积与面积比)；添加剂、构件的配筋率，以及混凝土受力状态等等。基于上述因素，国内外学者提出了多种预测收缩变形的计算模式。

美国混凝土学会(ACI)209委员会推荐的混凝土随时间的收缩可以用下式[1]表示：

(1)

式中：f和a对给定形状和尺寸试件时为常数，ACI建议a取1，f取35(湿养护)或55(蒸汽养护)；βcp，βh，βα，βs，βp，βce，βac分别是干燥前养护时间、环境湿度、体积-表面积比、混凝土配合比、坍落度、骨料含量、水泥用量、混凝土含气量等因素的影响系数。

澳洲规范(简称AS3600-1988)[2]中混凝土收缩的计算公式为：

(2)

式中：εsh，obs为基本收缩应变，其值为500×10-6～1 000×10-6，文献[2]推荐可取中间值700×10-6；K1为与尺寸、温度和湿度有关的混凝土收缩系数，其取值详见文献[2]。

欧洲混凝土委员会制定的规范CEB-FIP MC90中[3]，混凝土构件的平均收缩应变用下式表示：

(3)

式中：εcso为名义收缩系数(极限收缩变形)；βs(t，ts)为随时间变化的系数，具体取值及适用范围见文献[4]。

我国学者王铁梦教授根据多年的工程实践得出了经历任意时间的混凝土干燥收缩计算公式[5]：

(4)

式中：3.24×10-4为标准状态下混凝土的最终收缩，M1，M2，…，Mn为考虑各种非标准条件的修正系数。

美国的Z.P.Bazant教授在总结前人大量试验数据的基础上，于20世纪70年代末80年代初提出了BP系列模式。1995年又提出了更为简化、理论性更强的B3模式，其中收缩应变的计算公式[6]为：

(5)

式中：εsh，∞为干燥收缩应变的最终值(与ACI模式不同，由混凝土配合比及抗压强度、弹性模量等因素决定，但不包含形状、尺寸、湿度等因素)；kh为湿度相关系数；S(t)为与干缩时间t有关的干缩过程函数。B3模式考虑了水泥品种、水灰比、水泥用量、骨灰比及混凝土抗压强度等的影响。

除了以上列举的几种计算收缩的模式外，还有GL2000，GZ(1993)等模式。

2 实例计算及分析

本文选取北京某大厦西塔楼(44层、186 m高钢筋混凝土、钢梁组合楼板混合结构)9层顶的两根典型组合梁10GL-1和10GL-2为研究对象，进行了收缩影响下的附加挠度计算和现场挠度测量，并采用有限差分模拟分析软件FLAC3D对组合梁收缩效应做了相应的模拟分析。组合梁数据如下：GL-1，跨度11.385 m，型钢H340×250×9×14；GL-2，跨度9.81 m，型钢H294×200×8×12；钢梁材料为Q345B。混凝土为C40，板厚均为70 mm。梁上布置两排直径19 mm的钢栓钉连接件，排距60 mm，纵向间距195 mm，熔焊后高度为90 mm。钢栓钉连接件为ML15，屈服强度标准值(σ0.2)320 N/mm2，抗拉强度标准值(σb)400 N/mm2，伸长率(δ5)14%。9层顶钢梁结构平面布置见图1。

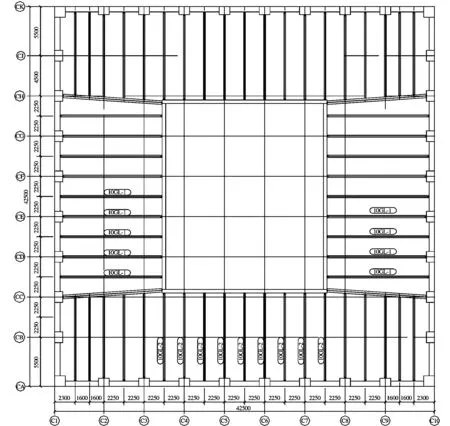
图1 9层顶钢梁平面布置Fig.1 Plan of 9-layer roof steel beam

2.1 收缩影响下的附加挠度计算及现场实测

基于文献[7-9]的推导，根据结构力学的方法，忽略剪切变形的影响，可得到考虑收缩应变εsh(t)影响的组合梁附加挠度计算式：

(6)

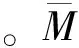
在现场对GL-1，GL-2进行了1年内9个时点的挠度测量。同时采用公式(6)对两根组合梁进行了一年内相应时点的挠度计算及1年后若干时点的挠度预测。计算结果及实测数据列于表1和2中。

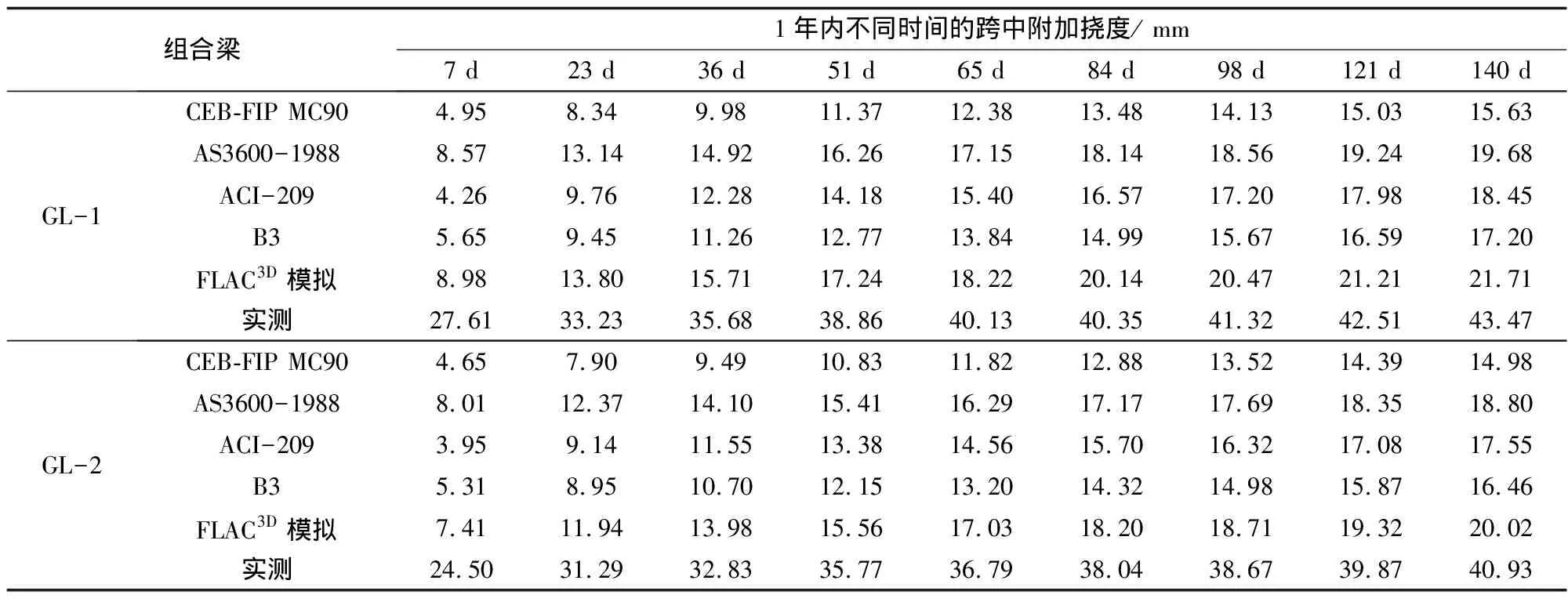
表1 组合梁(1年内)跨中附加挠度(收缩)计算及实测数据Tab.1 Calculated and measured data of additional mid-span deflection (shrinkage) (within one year) of composite beams

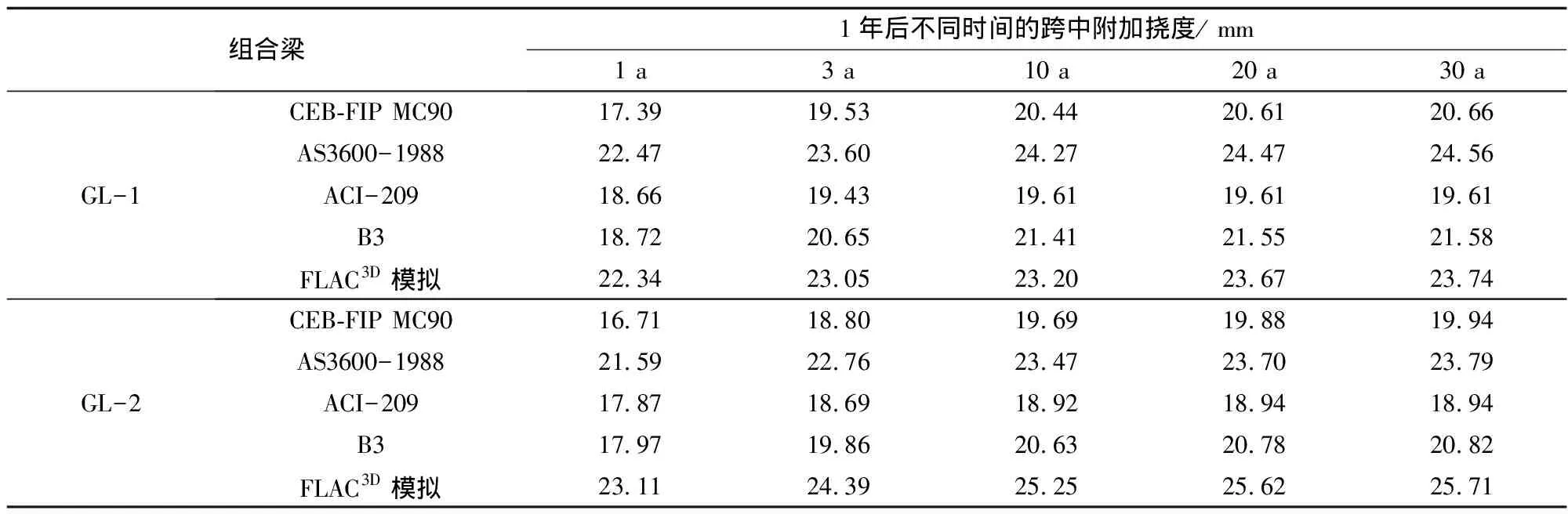
表2 组合梁(1年后)跨中附加挠度(收缩)预测数据 Tab.2 Predicted data of additional mid-span deflection (shrinkage) (one year later) of composite beams

2.2 FLAC3D数值模拟

本文采用有限差分模拟分析软件FLAC3D对组合梁的收缩附加变形进行数值模拟。FLAC3D利用显式有限差分方法为工程提供精确有效的分析，它提供了桩、杆、梁、壳等结构单元，可以解决诸多有限元程序难以模拟的复杂工程问题。FLAC3D软件还有内置的FISH语言，可以对软件进行二次开发，对计算过程进行交互式实时输入与控制；而且FLAC3D软件中还有非常丰富的塑性本构模型。

FLAC3D软件模拟组合梁混凝土翼缘的收缩时，考虑其泊松比和密度不随时间变化，根据不同时期的收缩应变εsh和其长期弹性模量Ecl，将收缩应变等效为相应的沿混凝土翼缘纵向的轴向力，在FLAC3D模型中进行代换即可得到不同时期的变形曲线。数值模拟中收缩应变按澳洲规范(AS3600-1988)选取。

组合梁附加挠度变形模拟见图2和图3。详细模拟数据列于表1和2中。根据表1和2的数据，给出GL-1和GL-2收缩附加挠度随时间变化图(见图4)。

图2 GL-1网格划分 图3 GL-1收缩附加挠度模拟 (84 d) Fig.2 GL-1 meshing Fig.3 GL-1 additional shrinkage deflection simulation (84 d)

(a) GL-1(1年内) (b) GL-2(1年内)

(c) GL-1(1年后) (d) GL-2(1年后)图4 GL-1和GL-2各模式收缩附加挠度及数值模拟挠度随时间变化 Fig.4 Time-varying curves of additional shrinkage deflection and numerical simulation of deflection of GL-1 and GL-2 in various modes

2.3 数据分析

根据以上图表信息进行数据分析可得：

(1)基于不同收缩模式的附加变形计算值和FLAC3D模拟值随时间的变化具有相同的趋势，并均在20年左右达到基本稳定。以20年为最终变形值，大部分收缩附加变形(70%～90%)均发生在龄期3～4个月内，与混凝土收缩的发展趋势相一致。且各模式30年收缩应变值均未超过700×10-6。

(2)由文献[7]可知，FLAC3D的模拟总值(考虑收缩、徐变、滑移)略大于实测值，但总体拟合程度较好。由前述图表可见，澳洲规范(AS3600-1988)模式的计算结果与模拟值最为接近，故AS3600-1988模式的计算结果与实测值也最为接近。

(3)采用CEB-FIP MC90模式进行计算时，计算过程较ACI-209和B3模式相对简单。但收缩开始时的混凝土龄期ts选择越早，其计算值越大。本文的计算数据为其最大计算值，但其计算值还是远小于其他几种模式的计算数据及模拟计算结果，其计算结果误差较大。

(4)ACl209模式收缩进程的时间函数采用双曲线函数表达式，其中的各参数均取为常数，未计入尺寸效应的影响，即该模式认为构件尺寸的变化仅对收缩终极值产生影响，这将导致对收缩值的低估。因此其计算精度也不够理想，且其计算过程中需考虑诸多因素，计算过程较繁琐。

(5)B3模式本质上也是双曲线函数表达式，且其收缩进程的时间函数式中计入了尺寸效应的影响。但其各项材料参数是建立在试验基础之上的经验公式，属于半经验半理论公式。要提高模式的预测精度，需将模式中各项材料参数的计算公式建立在一定的理论基础之上，这方面的研究尚待进一步开展。

(6)除AS3600-1988模式外，其他3个模式的计算中，要直接用到当地的平均相对湿度，该统计数据变异较大。以本文测量数据的时间段为例，在进行现场测量的140 d时间内，当地的月平均相对湿度的变化从36%到73%，使用该数据进行计算相对繁琐且难以准确。AS3600-1988模式采用相对简单统一的系数F1来考虑相对湿度的影响，计算简便易行。

(7)组合梁的长期变形主要由混凝土的收缩和徐变两部分引起。本文仅对影响组合梁长期变形的收缩因素进行了分析。式(6)中计算混凝土长期弹性模量Ecl时，采用按龄期调整的有效模量法，即降低弹性模量来考虑混凝土徐变的影响。

3 结 语

本文建立了考虑混凝土收缩应变的组合梁附加挠度计算式，计算结果表明，收缩附加变形引起的挠度可占到总挠度的近50%，且其影响主要发生在浇筑混凝土后的3至4个月内。因此，减小浇筑初期混凝土的收缩变形，是组合梁的长期挠度控制的有效手段。通过计算机模拟和各收缩模式下计算结果的对比分析，该计算式可用于组合梁的收缩附加挠度计算，收缩应变建议选用澳洲规范(AS3600-1988)模式。简化计算时，为充分考虑收缩对变形的影响，收缩终值可采用700×10-6。

在组合梁混凝土翼缘上部配置一定数量的钢筋，可增加翼缘板的刚度，还可以阻止混凝土的收缩，以减小混凝土收缩的影响。但这部分钢筋的作用很难准确计算，如何考虑这些钢筋的影响，是需要进一步研究解决的问题。

参 考 文 献：

[1]ACI209 R-82， Prediction of creep， shrinkage and temperature effects in concrete structures[S].

[2]AS3600-1988， Australian standard for concrete structures[S].

[3]Comite Euro-International du Beton. Ceb-Fip Model Code 1990(Concrete Structures) [S].

[4]朱伯芳. 混凝土的弹性模量、徐变度与应力松弛系数[C]∥水工结构与固体力学论文集. 北京： 水利电力出版社， 1988. (ZHU Bo-fang. The modulus of elasticity of concrete， creep and stress relaxation coefficient[C]∥Proceedings of the hydraulic structure and solid mechanics. Beijing： China WaterPower Press， 1988. (in Chinese))

[5]王铁梦. 工程结构裂缝控制[M]. 北京： 中国建筑工业出版社， 1997： 24-25. (WANG Tie-meng. Control of cracking in engineering structure[M]. Beijing： China Architecture & Building Press， 1997： 24-25. (in Chinese))

[6]林波. 混凝土收缩徐变及其效应的计算分析和试验研究[D]. 南京： 东南大学， 2006. (LIN Bo. Computing analysis and experimental study on shrinkage and creep of concrete[D]. Nanjing： Southeast University， 2006. (in Chinese))

[7]李达. 钢-混凝土组合梁在荷载长期效应组合下的变形研究[D]. 北京： 北京科技大学， 2006. (LI Da. Research on the deflection of composite steel-concrete beams under long-term load combination[D]. Beijing： University of Science and Technology Beijing， 2006. (in Chinese))

[8]樊健生， 聂建国， 王浩. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(Ⅰ)—试验及计算[J]. 土木工程学报， 2009， 42(3)： 8-15. (FAN Jian-sheng， NIE Jian-guo， WANG Hao. Long-term behavior of composite beams with shrinkage， creep and cracking (Ⅰ)： experiment and calculation[J]. China Civil Engineering Journal， 2009， 42(3)： 8-15. (in Chinese))

[9]樊健生， 聂鑫， 李全旺. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(Ⅱ)—理论分析[J]. 土木工程学报， 2009， 42(3)： 16-22. (FAN Jian-sheng， NIE Xin， LI Quan-wang. Long-term behavior of composite beams with shrinkage， creep and cracking (Ⅱ)： theoretical analysis[J]. China Civil Engineering Journal， 2009， 42(3)： 16-22. (in Chinese))

[10]潘立本， 张苏俊. 混凝土收缩与徐变的试验研究[J]. 河海大学学报， 1997， 25(5)： 84-89. (PAN Li-ben， ZHANG Su-jun. Prediction of shrinkage and creep in concrete[J]. Journal of Hohai University， 1997， 25(5)： 84-89. (in Chinese))

[11]胡狄， 陈政清. 从短期试验结果预测新建预应力混凝土梁收缩和徐变的长期效应[J]. 中国铁道科学， 2003， 24(3)： 44-49. (HU Di， CHEN Zheng-qing. Prediction of long-term effect of creep and shrinkage on newly-built prestressed concrete bridge based on short-term test results[J]. China Railway Science， 2003， 24(3)： 44-49. (in Chinese))

[12]聂建国， 刘明， 叶列平. 钢-混凝土组合结构[M]. 北京： 中国建筑工业出版社， 2005. (NIE Jian-guo， LIU Ming， YE Lie-ping. Steel-concrete composite structures[M]. Beijing： China Architecture & Building Press， 2005. (in Chinese))

[13]黄国兴， 惠荣炎， 王秀军. 混凝土徐变与收缩[M]. 北京： 中国电力出版社， 2012. (HUANG Guo-xing， HUI Rong-yan， WANG Xiu-jun. The creep and shrinkage of concrete[M]. Beijing： China Electric Power Press， 2012. (in Chinese))

[14]徐荣桥， 陈德权. 组合梁挠度计算的改进折减刚度法[J]. 工程力学， 2013， 30(2)： 285-291. (XU Rong-qiao， CHEN De-quan. Modified reduced stiffness method for calculating the deflection of composite beams[J]. Engineering mechanics， 2013， 30(2)： 285-291. (in Chinese))