基于ANSYS的压力容器表面凹坑缺陷安全评定分析

，,2，，

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.河北省交通安全与控制重点实验室，河北 石家庄 050043；3.石家庄铁道大学 土木工程学院，河北 石家庄 050043)

0 引言

在当代化工产业中，大型罐体常被用于化学腐蚀液体、气体的公路汽车车载运输。为了保证其安全运行，我国每年都需花费大量的资金对这种运输容器进行检修，对存在缺陷的罐体进行报废更新或者修复处理。

在所有罐体缺陷当中，凹坑是最为常见的表面缺陷。它可以由容器在制造、焊接和安装过程中产生的表面或近表面缺陷经打磨后形成，也可以由气体或液体腐蚀形成[1-2]。凹坑缺陷的存在，必然会降低容器的强度，威胁罐体的安全运行，处理不当极易诱发事故。但值得注意的是，并不是所有含凹坑缺陷的罐体都要进行补焊返修处理，不必要的补焊返修只会造成大量的人才、物力以及财力的浪费。在某些情况下，罐体上的凹坑缺陷是允许存在的，只需要将这些凹坑部位打磨光滑，这些罐体就可以继续使用，不会影响其安全运行[3]。可见系统地研究凹坑缺陷的评判标准,以判断具体条件下凹坑缺陷对罐体强度的影响程度,在保证罐体安全运行的前提下，减少大量不需要的补修，节约资源，不但是安全生产的要求也是经济建设的需要[4]。

以AC15-01-00型液氨槽罐车筒体作为研究对象。将筒体表面凹坑规则化处理成椭球形凹坑，建立轴向和周向凹坑缺陷的三维几何模型和有限元模型，施加边界条件和载荷后，调整凹坑几何参数，在综合考虑压力容器表面凹坑应力理论计算以及单元类型和网格尺寸所造成的仿真偏差基础上，将与许用剪切应力差量小于5%的最大剪切应力值作为仿真终止判据，得到凹坑各几何参量的阈值。最后利用最小二乘法处理阈值并绘制出两类凹坑缺陷的安全评估参考曲线。筒体的内径为2 180 mm，外径为2 212 mm，厚度为16 mm。

1 凹坑缺陷的规则化处理办法

筒体结构表面的不规则凹坑缺陷按其外接矩形将其规则化为长轴长度、短轴长度及深度分别为2A，2B及C的椭球形凹坑，凹坑底部曲线规则化为抛物线。其中，长轴2A为凹坑边缘任意两点之间的最大垂直距离，短轴2B为平行于长轴且与凹坑外边缘相切的两条直线间的距离，深度C取凹坑的最大深度(见图1)。

图1 凹坑缺陷表征示意图

2 筒体表面凹坑的应力计算

筒体内径Di和筒体厚度t已知，则在恒定内压p作用下筒体的轴向和周向薄膜应力分别为σa=pDi/4t和σc=pDi/4t。设经规则化处理后的凹坑长半轴为A，短半轴为B，凹坑深度为C，图2，图3分别为筒体轴向凹坑和周向凹坑示意图[5]。

图2 规则化轴向凹坑示意图

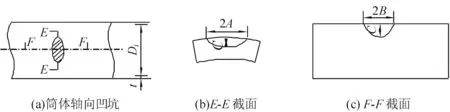
图3 规则化周向凹坑坑示意图

对于轴向凹坑，凹坑中心最大合成应力为[6]

{

σam=σabm+σamm+μσcbm

σcm=σcbm+σcmm+μσabm

(1)

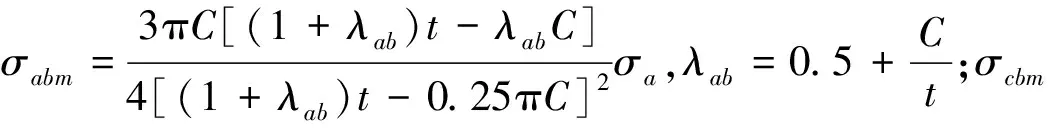
对于周向凹坑，同样可得到上述各应力的计算式，只需取：

3 计算机建模与仿真

在筒体外壁建立具有对称结构的椭球形凹坑。根据圣维南原理考虑筒体和凹坑结构的对称性，对带有表面轴向凹坑或周向凹坑缺陷的筒体进行分析时可取凹坑结构的四分之一,剖分面位于结构的对称面处,计算时在对称面上施加对称约束。

在建立筒体凹坑分析模型时，选用10节点SOLID187 4面体单元,采用自由网格的方法进行划分，同时添加区域网格尺寸控制，将凹坑附近的结构网格进行细化[7]。筒体材料为16MnR，密度为7 850 kg/m3，弹性模量为209 GPa，泊松比为0.28，材料屈服极限为345 MPa，许用应力为230 MPa。由于像低碳钢这一类的塑性材料，在单向拉伸试验时材料是沿斜截面发生滑移而出现明显屈服现象的，所以结构的最大剪切应力值是否达到许用应力可以成为有效的仿真终止判据。对模型内壁施加2.16 MPa的工作压力，对结构端面施加全约束，选择输出最大剪切应力值。

经试算，应力仿真结果一定程度取决于区域细化网格的尺寸。为确定区域网格的具体尺寸，任取一几何尺寸的凹坑，以筒体表面凹坑合应力计算式的理论值为依据，通过调整区域网格尺寸，使最大合应力仿真值与理论值的误差量不超过2%，取此时的区域细化网格尺寸进行后续仿真获得最大剪切应力。通过比较不同网格尺寸仿真算例得出：当区域细化网格的尺寸为0.3 mm时，最大合应力仿真值与理论值基本吻合。当A=50 mm、B=50 mm、C=13 mm以及网格尺寸为0.3 mm时，最大合应力的仿真解为457 MPa，理论解为465 MPa，误差为1.7%。

3.1 轴向凹坑仿真结果

轴向凹坑的有限元模型如图4(a)所示。在椭球凹坑的几何参量中，深度(C)与形状(B/A) 是影响筒体结构强度的两个重要因素。在恒定内压下，最大剪切应力的大小与C、B/A、A3个参量相关，采用特定参数法找出最大剪切应力与这些参量的相互关系，即选择C、B/A和A3个参量中的任意2个参量为恒量，另一参量为变量，获取最大剪切应力值与此参量的关系。当C=14 mm、B/A=1时，A取值90 mm、80 mm、70 mm、60 mm时，对应的最大剪切应力分别为689 MPa、579 MPa、488 MPa、385 MPa。当B/A=1、A=80 mm时，C取值15 mm、14 mm、13 mm、12 mm时，对应的最大剪切应力分别为302 MPa、294 MPa、273 MPa、265 MPa。当C=14 mm、A=80 mm时，B/A取值1、0.8、0.6、0.4时，对应的最大剪切应力分别为579 MPa、623 MPa、667 MPa、709 MPa。

图4 有限元模型

可以看出，最大剪切应力与A、C的随动关系为同增同减，而与B/A的随动关系则相反。根据随动关系，调整参量以获取与许用应力差量小于5%的最大剪切应力，具体数值如表1，表2所示。其安全区域为曲线，以及通过曲线右端点与纵轴的平行线，和两坐标轴所围城的区域。当凹坑的深度为9 mm、8 mm以及7 mm时，短长轴比为1时，A达到极限取值时，最大剪切应力也不超过230 MPa，由此可判定当凹坑的深度为9 mm、8 mm和7 mm时，B/A的最大取值是小于 1的某个数值。对C=6 mm的仿真结果显示，当B/A取极小值并且A取极大值时，最大剪切应力值始终小于200 MPa，由此可推断出，当凹坑深度C≤6 mm时候，凹坑缺陷对压力容器的结构强度没有太大的影响,封头在正常工作条件下是安全的。以B/A作为横坐标，A为纵坐标，绘制如图5所示不同深度轴向凹坑的安全评估曲线。由于当B/A<0.2时，凹坑演变为沟槽，在此不做研究，所以初始取值定为0.2。

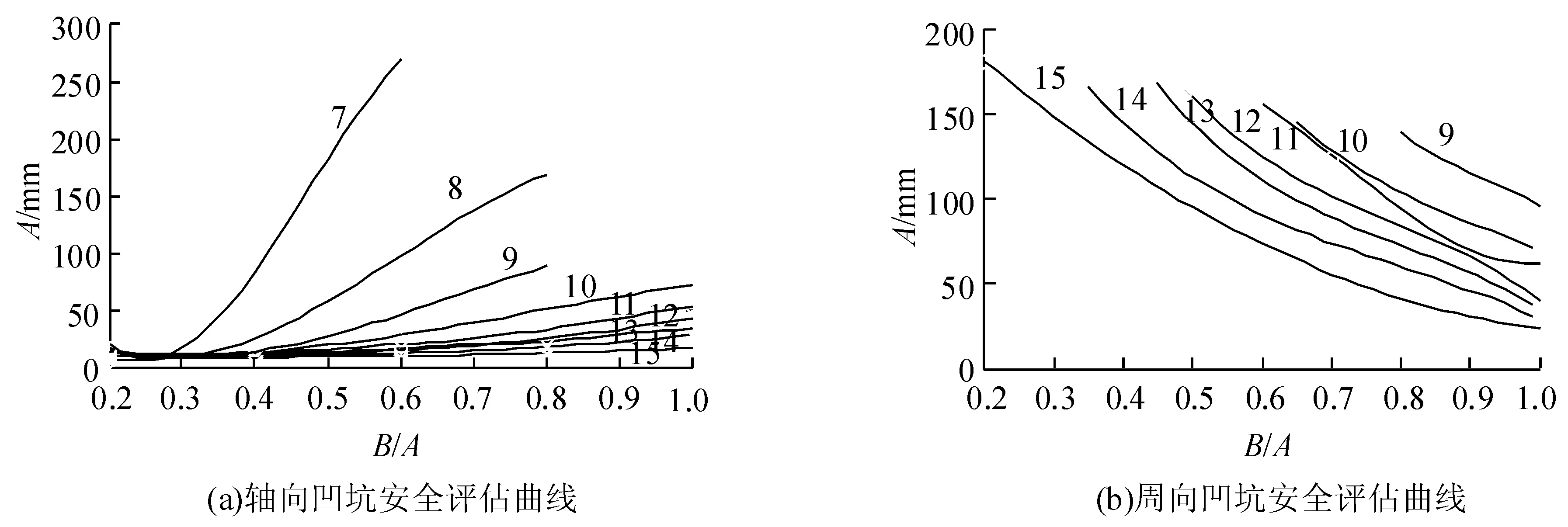
图5 凹坑安全评估曲线

表1 最大剪切应力与许用应力差量小于5%时轴向凹坑A、C、B/A的数值(a)B/AAC=15 mmC=14 mmC=13 mmC=12 mmC=11 mmC=10 mm11729354454710.81318242635570.61113141618250.4811121315160.27910111314

表2 最大剪切应力与许用应力差量小于5%时轴向凹坑A、C、B/A的数值(b)C=9B/AAC=8B/AAC=7B/AA0.8860.81680.62640.7770.71400.52000.6380.6950.4580.4170.4270.3350.2150.2160.217

3.2 周向凹坑仿真结果

周向凹坑的有限元模型如图4(b)所示，经仿真验证，最大剪切应力与A、C以及B/A的随动关系均为同增同减，最大剪切应力与许用应力差量小于5%时，A、C、B/A3个参量的具体数值如表3所示。由于凹坑A达到极大值时，B/A只需取一个较大的值就能满足仿真终止条件，此值即B/A取值的下限,按照均布原则选择B/A的取值。另外，对C=8 mm的凹坑仿真结果显示，当B/A和A都取极大值时，最大剪切应力始终小于200 MPa，由此可推断，当周向凹坑深度只有8mm的时候，筒体在正常工作下是安全的。根据表3所示的数据，建立筒体周向凹坑安全评估参考曲线(见图5(b))，其安全区域为曲线，以及通过曲线左端点与横轴的平行线，和两坐标轴所围城的区域。

表3 最大剪切应力与许用应力差量小于5%时周向凹坑A、C、B/A的数值C=15B/AAC=14B/AAC=13B/AAC=12B/AAC=11B/AAC=10B/AAC=9B/AA1231301351401611711960.8450.8560.8710.8830.9720.9830.951070.6680.6980.7920.71040.8910.81090.91160.41240.41330.61090.61230.71280.71240.851250.21810.351740.451680.51610.61550.651480.8139

4 结论

(1)对于AC15-01-00型液氨槽罐车筒体，当轴向凹坑和周向凹坑深度足够小，筒体都是趋于安全的。其中轴向凹坑的安全深度为6 mm，周向凹坑的安全深度为8 mm。

(2)周向凹坑对筒体结构强度的影响比轴向凹坑对筒体的影响小。原因是对于薄壁容器的圆筒部分，其纵截面上的应力较横截面上的应力大一倍左右，圆筒部分发生强度破坏将沿纵向发生破坏。

在工程实际应用中，相关工作人员合理规则化处理凹坑以后，根据凹坑位置、形状等因素选取合适的安全判定曲线对凹坑进行安全判定，能大大提高工作效率，节省工期，产生一定的经济效益。

参 考 文 献

[1]崔文勇，任巧贤，常晓军,等. 内压厚壁容器外壁表面凹坑应力场有限元分析[J]. 山西机械，1999,26(2):41-45.

[2]徐佩珠，李毅，周道祥. 压力容器表面凹坑应力集中的试验研究[J]. 压力容器，1999,10(2):42-45.

[3]陈钢. 含凹坑缺陷压力容器极限与安定性数值分析[D]. 北京:清华大学工程力学系，1994.

[4]潘清，白继钢. 关于压力容器壳体上存在凹坑缺陷评定方法的探讨[J]. 北京化工大学学报，2000,107(2):32-34.

[5]谢铁军，刘东学，陈钢,等. 压力容器应力分布图谱[M]. 北京:北京科学技术出版社,1994.

[6]李思源，温旭东，李祚成. 压力容器表面凹坑和沟槽的应力计算[J]. 石油化工设备，1995,24(5):26-31.

[7] 李兵，菜保青. 基于ANSYS 对压力容器管板的有限元分析[J]. 煤矿现代化，2008(2):44-45.