某大坝安全监测资料的反馈分析

王建国

（新疆伊犁河流域开发建设管理局，新疆 伊宁 830000）

某大坝安全监测资料的反馈分析

王建国

（新疆伊犁河流域开发建设管理局，新疆 伊宁 830000）

为了全面了解和监控枢纽的建设和运行情况，特别是拦河大坝的变形、渗流及应力发展，枢纽中埋设了大量观测仪器并进行了持续的监测，并取得了丰富的观测资料，这些资料为该坝的反馈分析提供了必要的基础。根据大坝监测资料整理及分析成果，对某心墙堆石坝进行了有限元变形渗流反馈，并预测和评价坝体今后的变形和渗流安全。

渗流反馈；变形；渗流安全；安全监测

1 工程概况

某水利枢纽拦河坝坝型为粘土心墙堆石坝，坝顶高程 1 003 m，最大坝高 108 m，坝顶长度 362 m，坝顶宽 12.0 m，上游坝坡 1∶2.5，下游综合坝坡1∶2.33，心墙防渗体顶高程 1 001.0 m，宽 6.0 m，心墙上下游边坡1∶0.3。

2 计算方法及参数

在心墙堆石坝的施工、蓄水过程中，坝体，特别是心墙内的土骨架变形和渗压之间存在比较复杂的耦合关系，基于 Biot固结理论的有效应力计算分析方法是最接近实际情况的分析方法。

在计算分析中选用国内比较通行的沈珠江双屈服面弹塑性模型（简称沈珠江模型），模拟土骨架的应力应变关系，并采用增量迭代法进行计算。计算中未考虑筑坝材料的流变和湿化。

沈珠江双屈服面模型采用如下弹塑性增量应力应变关系，按（1）-（2）式计算：

式中［］Dep为弹塑性模量矩阵，对于平面应变问题Ge和 Be分别为弹性剪切模量和体积模量，按式（3）～（4）计算：

v 为泊松比，可以取 1/3。Eur按照式（4）计算

Pd为大气压力 1.01×105kPa。A1和 A2为 2 个塑性系数，按式（5）-（12）计算：

式中：

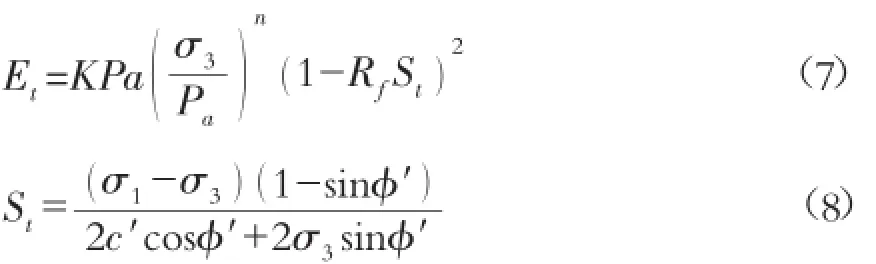
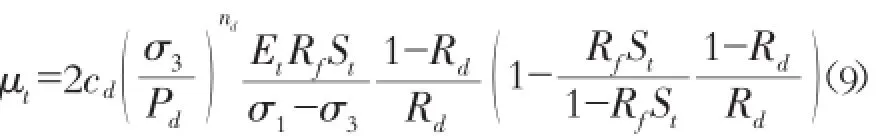
该模 型 共有 9 个 计 算参 数 c′，φ′，K，Kur，n，Rf和 cd，nd，Rd，可由一组不同围压下的三轴试验得出。模型采用以下双屈服面：

式（11）和式（12）同时成立表示全加荷，同时不成立表示卸荷，其中之一成立表示部分加荷。如果A1=A2=0，弹塑性矩阵将退化为弹性矩阵。

分析中假定土体中的孔隙气以气泡形式封闭或溶解在孔隙水中，把水气混合体当作一种可压缩的流体对待，认为流动服从 Darcy 定律，并取渗透系数为常量。含气水的压缩系数按式（13）-（14）考虑：

其中，ns为孔隙率；Sr为饱和度；c0为无气水压缩系数，其值为 4.7×10-7kPa-1，Pw为孔隙水压力。饱和度按 H ilf公式计算：

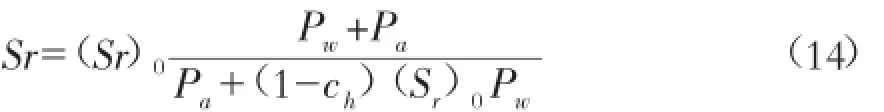
其中，（Sr）0为填筑时的初始饱和度；ch为亨利溶水系数，常温下可以近似取 0.02；Pa为大气压；Pw为孔隙压力。

3 计算概况

对拦河大坝的监测以河床最大 0＋175 m 断面为主监测断面，并以左岸 0＋123.5 m 断面和右岸0＋223 m 断面为副监测断面，两岸 0＋060 m 和 0＋270 m 断面的监测用于考察安排开挖较陡处的拱效应。

参考实际的施工和蓄水过程，计算过程模拟了实际施工、蓄水运行的全部过程（从 2003 年 10月开始施工，2005 年 6 月填至坝顶；同年 6 月 25日开始蓄水，一直到监测资料结束时，即 2006 年 1月），共计 36 个计算级，分为 3 个阶段。

第一阶段（1-5 级）：从 2003 年 10 月至 2004年 5 月，模拟了围堰档水的干填筑期，期间库水位保持为 920.70 m，坝体填高至 922.2 m。其中包括一个计算级，坝体填筑高程和库水位均不发生变化，为 2003 年底到 2004 年初约 3 个月时间的冬季停工期。

第二阶段（6-22 级）：从 2004 年 5 月至 2005年 6月，模拟坝体一边填筑一边蓄水的过程，期末，坝体填筑到顶（1 002.0 m 高程），水库蓄水至945.70 m。其中也包括一个计算级坝体填筑高程和库水位均不发生变化，为 2004 年底到 2005 年初约4个月时间的冬季停工期。

第三阶段（23-36 级）：从 2005 年 6 月至 2006年1月为蓄水期，模拟水库蓄水、水位上升的过程，该段时期内库水位自 945.70 m 上升至 986.63 m，6 月内水位上升超过 40 m。

第三阶段后，假定库水位按照原先的速度继续上升，直到达到正常蓄水位 995.0 m，这个阶段的模拟用 37～39 级的计算来完成。

为预估水位骤降、骤升条件下坝体的变形渗流情况，在第四阶段结算后，还增加了 2 段各 3 级针对虚拟情况的计算，以考察非常运用情况下坝体的变形渗流情况。每段分析前后均安排一段长2年的时间用以消散超静孔压，以得到比较稳定的计算初始状态。对于库水位的骤升骤降，国内尚无明确限制。但为了体现极限情况，模拟中假定7 d内水位发生骤升骤降，范围设定为死水位 964.0 m～正常蓄水位 995.0 m 共 31 m 的区间。

坝体填筑分期情况，及填筑过程与库水位上升的关系，见图 1。

图1 填筑过程与库水位上升关系

4 计算分析成果及其分析

4.1 填筑期的反馈分析

计算的反馈分析主要针对坝体填筑期进行，即上述第一和第二阶段。坝体填筑完成时的沉降分布，最大沉降发生在坝高 1/3～1/2 范围内，心墙沉降量大于坝壳沉降量，与实测一致。最大沉降发生的位置比一般土石坝中最大沉降发生的位置略低，原因在于堆石坝上下游坝坡均比较缓。坝体中不同高度处的计算沉降和实测沉降不仅在大小上符合较好，并且其沿深度的变化规律也非常接近。坝体实测最大沉降为 422 mm，计算最大沉降为450 mm，两者发生高程基本一致。坝体沉降率小于0.5%，说明该坝施工质量较好。沈珠江曾发现，对于狭窄河谷中的土石坝，三维计算值约为二维的 75%～80%，考虑心墙堆石坝坝址河谷宽度不太窄，可以认为上述计算和实测最大沉降之间的差异正体现了二维计算条件与实际三维条件的差异。

坝壳中有效大主应力最大值为 2.09 MPa，有效小主应力最大值为 1.10 MPa；心墙中有效大主应力最大值为 1.32 MPa，有效小主应力最大值为0.79 MPa。根据断面应力分布可见，由于心墙沉降大于坝壳，坝壳对心墙存在明显的拱效应，这一方面加大了坝壳所受竖直应力，另一方面则减小心墙的竖向应力。拱效应在较低高程处比较明显，而较高高程处逐渐趋缓。同时，由于心墙下游侧地形凸起，下游侧拱效应较上游侧更为明显，说明心墙上下游侧开挖地形的差异对心墙的应力状态会有较大的影响。尽管心墙两侧存在一定的拱效应，但是心墙中的有效应力仍然保持较高水平，因此，发生水平、竖直裂缝或水力劈裂的可能性很小。

坝体填筑完成时，坝体中应力水平分布比较均匀，这说明坝体设计合理，不会发生剪切破坏，整体稳定性比较容易保证。应力水平最高值为 0.5，发生在库水位线下的心墙上游侧，原因在于心墙透水性较低，受到库水推力作用时向下游发生弯曲变形，因而接近心墙的上游坝壳由于围压减小而应力水平增高。

4.2 蓄水期的模拟分析

末期（2006 年 1 月）坝体的沉降和孔压分布已有监测结果。假定保持原水位上升速度，首次蓄水至正常蓄水位时坝体的沉降和孔压分布。继续蓄水，直至蓄到正常蓄水位时，坝体的沉降较竣工时不会有大的变化，这与实测结果是一致的。同时，水位不断上升的过程中，心墙内孔隙压力没有明显积累，从上游侧到下游侧，孔隙压力沿着心墙迅速降低，该分布符合一般规律。

4.3 水位骤降、骤升预测

在模拟蓄水至正常蓄水位 995.0 m 后，采用反馈得到的参数预测了经历极限运用条件时坝体的安全性。

经过近5年的孔隙压力稳定后得到的孔隙压力分布，孔压分布非常接近，这说明在按照实际蓄水速度进行蓄水时，库水位上升造成的超静孔隙水压力消散较快，心墙中已明显形成稳定渗流。

水位在 7 d 内骤降、骤升 31 m 刚刚完成时坝体的计算孔隙压力分布。由于水位升降速度过快，心墙内出现了比较明显的孔压变化的滞后现象。但是，由于心墙中孔压没有大的累积和增长，孔压值比总应力小很多，同时，水力梯度较稳定渗流期增大不多，因此，心墙发生水力劈裂和渗透破坏的可能性不大。

骤升骤降发生后，坝体变形没有大的增长，应力水平略有提高，水位骤降后，应力水平达 0.5 以上的区域范围有所扩大，但仍局限于心墙下部及其上游侧。水位骤升后，应力水平较刚填筑完成时变化较多，主要体现在心墙上部及其下游侧应力水平下降，而心墙中下部及其上游侧，特别是心墙中部紧贴心墙的坝壳部分应力水平大幅上升，上游坝面附近应力水平也有较大上升。出现此现象的原因在于短期内水位上升时，心墙来不及透水而在水荷载作用下向下游弯曲，从而下游侧由于受到挤压而围压升高，剪应力水平下降；而上游侧则由于侧向释放而围压降低，从而导致剪应力水平上升。

5 结论

1）反演分析说明，大坝变形、孔压及应力分布符合土石坝的一般规律。

2）计算分析较好地反映了大坝的沉降变形及渗压分布，计算值与实测值均符合很好。在反演分析基础上的预测计算说明，蓄水至正常蓄水位后，坝体沉降变形较竣工期变化不大，同时，心墙仍能继续承担绝大部分水头。

3）无论竣工期还是蓄水期，坝体最大沉降均小于 0.5%；同时，坝体内部剪应力不高，且分布均匀，说明坝体设计合理，施工质量较好，变形已基本稳定，长期来讲不会出现坝体变形或坝坡稳定问题。

4）心墙内不会出现大幅度的孔压积累和增长现象，孔压整体水平较低，且消散比较迅速，不会对坝体安全造成影响。

5）坝壳对心墙存在一定拱效应，但不明显。心墙靠近下游坝底处坝壳与心墙相互作用较大，但心墙内绝大部分位置孔压水平较低，因此心墙中大、小主应力均能保持较高数值，坝体内不具备出现水力劈裂的应力条件。

6）在水位骤升、骤降条件下，心墙同样不具备发生水力劈裂的应力条件，心墙内水力坡降不大，不具备发生渗透破坏的水力条件。坝体没有明显大幅变形出现，虽然坝体部分区域剪应力水平增长较高，但区域较小，坝体的变形和稳定安全性均能基本保证。

7）变形渗流耦合的计算分析说明，心墙堆石坝的设计合理，在竣工期、蓄水期及极限运用条件下都能基本保证其安全性。

［1］李彦军，郭秀兰，等.大坝安全监测技术［M］.西安：西安地图出版社，2000.

［2］冯小磊，华锡生，黄红女.观测值序列的粗差探测方法［J］. 水 电 自动化 与 大 坝监测 ，2006，30（3）：56～59.

［3］陈龙，李婷婷，顾冲时.包络预测大坝监测值及监控指标研究［J］. 水电自动化与大坝监测,2004,28(5)：36～38.

［4］李庆扬.数值分析［M］.北京：清华大学出版社，2006.

TV698

B

1002－0624（2014）07－0059－03

2014-05-12