不确定条件下耦合 S-P 水质模拟的水资源管理模型建立研究
李淑玲,李贵阳
(1.辽宁省水文局,辽宁 沈阳 110003;2.辽宁省水文局沈阳分局,辽宁 沈阳 110003)
不确定条件下耦合 S-P 水质模拟的水资源管理模型建立研究
李淑玲1,李贵阳2
(1.辽宁省水文局,辽宁 沈阳 110003;2.辽宁省水文局沈阳分局,辽宁 沈阳 110003)
本文通过引入区间不确定性参数,并结合 S-P 一维水质模型,构建了改进的不确定水质预测模型,并将其预测结果作为考虑不确定参数的水资源管理模型的边界条件,以此形成不确定条件下耦合 S-P 水质模拟的水资源管理模型。 通过案例分析,具体描述该模型的应用条 件 和使 用方法 ,采用交 互式算 法对 建立的 耦合 ITSP-SP 模型 进行 求 解,得到 不确 定 参数的稳定区间解,从而为相关决策者制定水资源管理方案提供理论依据,同时通过约束条件,还可以核算出水量分配变化条件下相应的水质波动情况。
水质模型;水资源管理;S-P 模型
目前,在水资源管理中,主要利用数学模拟优化模型解决水资源管理中的水质水量问题,即通过对边界条件及模型参数的合理假设,然后进行优化求解,形成定量的水资源管理方案[1-2]。然而,在现实水资源管理中,模型中的参数往往具有不确定特征,对不确定参数进行定值假设往往使得水资源管理决策者在管理过程,不能有效地判断需水用户需水量、污染物排放和经济效益可达范围,从而导致由确定性模型得来的单一决策与实际情况产生偏差[3-4]。因此,本文在传统的水资源管理优化模型基础上,通过引入区间不确定性参数,并结合 S-P 一维水质模型,构建基于水质模拟的不确定水资源管理模型,为相关决策者制定水资源管理系统提供理论依据。
1 模型构建
1.1 改进的水质预测模型
河流中化学需氧量(COD)、溶解氧(DO)和生化学氧量(BOD)是反映河道内水体污染的重要指标,BOD 代表一定时间周期内可生物降解的有机物含量,COD 则表示在一定时间周期内包括 BOD以及不可生物降解的有机物和无机物含量。由此可知,河道的自然耗氧主要与河道内 BOD 指标成显著正相关关系,而河流 COD 浓度高则可能由其它无机还原性物质所致,因此,BOD 和河流的水质状况息息相关,更能反映河流的有机污染情况。
基于所研究区域水功能区设计流量较小、枯水期水面较窄的实际情况,同时该区域各用水单位水体污染物排放主要以有机物为主,用 BOD 指标可以更好地实现企业污染排放和河道内的水质监测,同时还满足 S-P 模型的应用条件[5]。在综合考虑BOD衰减和 DO 复氧的基础上,具有 m 个废水排放源的传统 S-P 氧亏值和 BOD 模拟预测模型可表述为:

其中,j代表第 j个河段;L0为河段的背景 BOD 值,mg/L;Ln-1和 Ln分别代表河段 n-1 和 n 起始处的BOD 负载;kd为河流中的耗氧速率常数(d-1);ka为复氧速率常数(d-1);Dn-1和 Dn分 别为河段 n-1 和n 处的氧亏值;tj是河流流过河段 j的时间单位;∂i是区域 i处的 BOD 去除效率;BODi是区域 i处的BOD 排放总量。考虑到现实中的模型参数如 BOD去除率、河流流动时间和背景 BOD 值等由于人为影响、自然因素和监测手段等不确定因素影响,呈现不确定特征,而这些参数通过观测获取数据进行概率分布或模糊隶属度表征较为困难。因此,本文利用区间参数对模型中的不确定参数进行表征,由此可得改进的 S-P 模型(ISP)为:
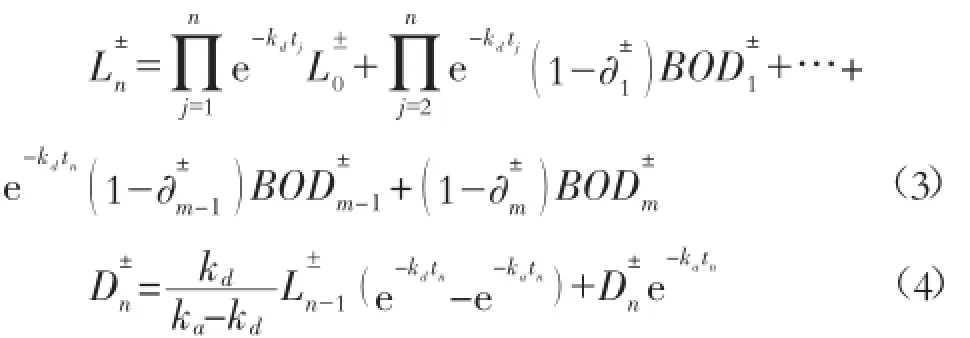
其中,L±n,L±
0,∂±
j,BOD±
j和 D±n分别为相应的区间参数。
1.2 水资源管理优化模型
考虑到小流域水资源管理决策者从水源地给多个用户供水,而这些用户在制定年度计划过程中需要知道他们能获得多少水量(水量对他们的计划产生影响:如果不能被供给足够的水量,他们就必须缩减扩展计划)。为求得该区域济活动利益最大化问题(所要建立的规划的目标函数)。先给每一个用户许诺一个水量,如果满足了用户,则会产生净利润;否则,要么从更贵的水源地调水来满足用户需要,要么用户缩减计划以减少用水量,但是两个方案都会损害该地区的经济利益。同时考虑现实水资源系统中的不确定问题,以此建立区间不确定两阶段优化模型(ITSP)为:
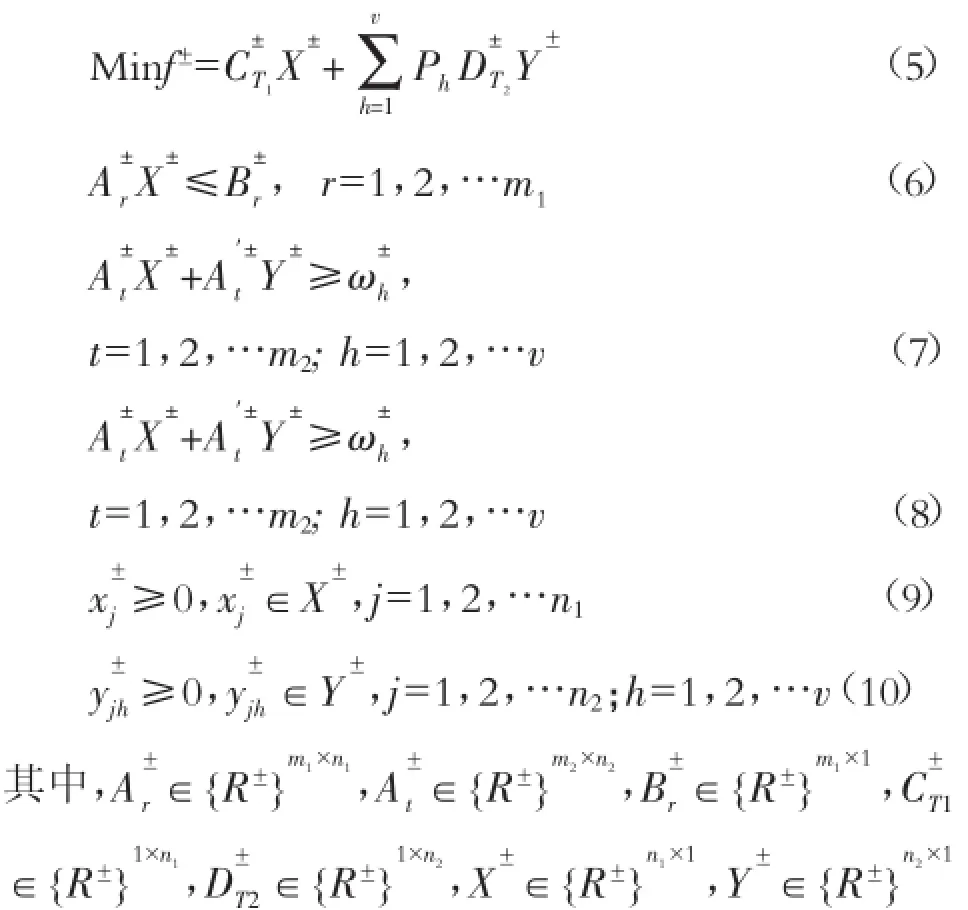
和{R±}代表以区间数表示的模型参数矩阵或决策变量。
2 实际案例分析
2.1 模型建立
某区域水资源管理者负责将具有随机特性的上游来水分配到两个需水用户(主要排放污染物均为有机污染物),每个用户在河道上分别设置一个排污口,并假设污染物瞬间均匀稀释。为了满足排放要求,每个用水区域所产生的一部分废水必须经集中处理后排放。引入前面所述模型在满足各段水质要求的条件下实现水量合理分配,并使系统收益最大。根据所给条件,将 ISP 作为 ITSP 模型的边界条件进行耦合,得到如下 ITSP-SP 模型:
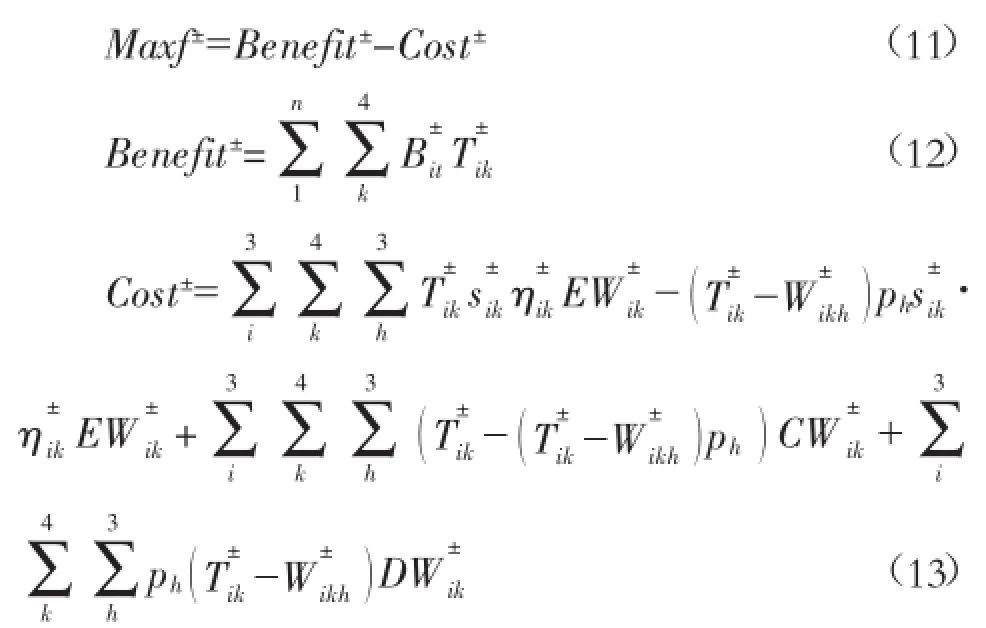
目标函数:其 中 :T±ik为 第 k 时 期 、第 i区 域 计 划 分 配 的 用 水 量(第一阶段的决策变量,计算过程中用 y 表示,T±
ikh=T-ikh+y△Tikh),W±ikh为当总水量为 Q 时(ph概率)第k 时期、第 i区域的实际分配水量(随河水流量变化,第 二 阶 段 的 决 策 变 量);B±ik为 第 k 时 期 、第 i区域每 单 位 用 水 量 所 获 得 的 利 润 ;CW±ik为 第k时 期 、第 i区 域从 河 流中 取 水 所 花 费 的 费 用 ;DW±ik为 第k时期、第 i区域每减少单位水量所减少的利润(DW±ik>B±ik);EW±ik是 第 k 时 期 、 第 i区 域 每 单 位 污 水 的 处理 费 用(达 到 排 放 标 准);s±ik为 第 k 时 期 、第 i区 域每单位用水量的污水产生率;ηik为第 k 时期、第 i区域污水的集中处理率。
约束条件:
1)用水总量约束:
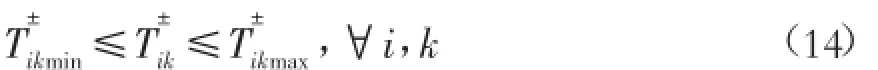
2)河流最大取水量约束:
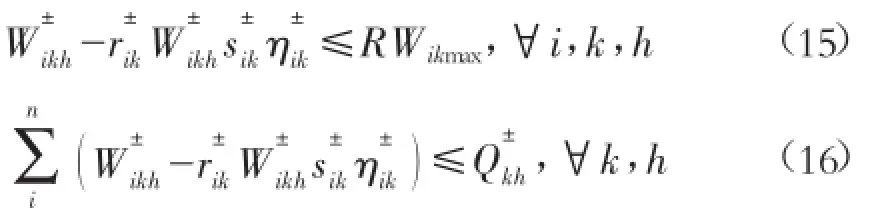
其中 :Tikmin为计划最低用水 量 ;Tikmax为计划 最 高 用水量 ;RWikmax为第 k 时期、第 i区域所允许的最大河流取水量;Qkh为第 k 时期在 h 水平下的河流总流量。
3)污染物排放总量约束:
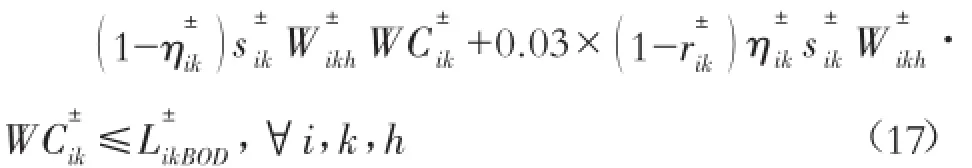
其 中 :WC±ik为 第 k 时 期、 第 i区域 每 单 位 污 水 的 原始 BOD 浓度 ;L±为第 k时期、第 i区 域 的 BOD
ikBOD排放限制,排放的污水浓度要求满足《污水综合排放标准》中的二级标准 30mg/L。
4)第 i区域所在监测断面处的 BOD 浓度约束:

其中,tj为河流流经河段 j的时间单位,BOD0为河流 的 本底 BOD 浓 度 。R±jkBOD是河 段 j 的 尾端 所允 许的 最大 BOD 值,R±jkBOD≤6mg/L。BOD±i是第 i区域排入河流后的 BOD 浓度。
5)所允许的最大氧亏值约束:
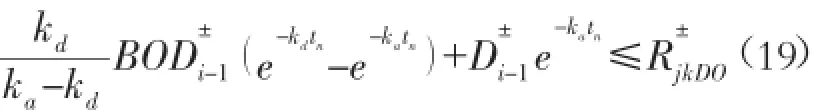
其 中 ,R±jkDO是 河 段 j 的 尾 端 所 允 许 的 最 大 氧 亏 值 ,R±
jkDO≤3mg/L;BOD±i-1是 第 i-1 区 域 排 入 河流 后 的BOD 浓 度 ;D±i-1是 河 段 j-1 尾 端的 氧亏 值。
6)产品产量约束:
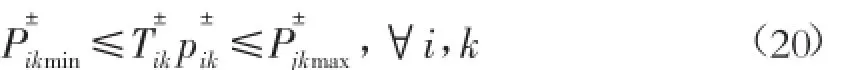
其中:P±ik是 第 k 时 期、 第 i区域 每单 位用 水量 所 生产 的 产量 ;Pjkmin是 第 k 时 期、 第 i 区 域 所 必须 达 到的 最 低 产 品 总 量 ;P±jkmax是 第 k 时 期 、 第 i 区 域 所 能达到的最高产品总量。
2.2 模型求解
通过交互式算法[6]将 建 立 的 ITSP-SP 模型转化成两个分别对应上界和下界期望目标函数的子模型,进而获得稳定的区间解,从而在潜在波动区间内,为决策者提供水资源分配方案,同时通过约束条件,还可以核算出相应的水质波动情况。
3 结 语
该研究将改进的水质模型(ISP 模型)与不确定两阶段模型(ITSP 模型)相耦合,构建形成了基于 S-P 模拟的水资源管理(ITSP-SP)模型。其中:
1)模型充分考虑现实水资源系统中参数不确定性问题,将改进的水质模拟模型结果作为水资源优化配置的边界条件,有效地实现水资源管理中兼顾水质水量的目的。
2)该模型可以有效地处理水资源分配过程中以区间参数表征的不确定性问题,决策者可以在满足水质环境约束的前提下,根据个人偏好调整水资源分配方案,并最终实现系统利益最大化。
3)该模型还可以根据具体湖泊、河流情况,改变作为边界条件的水质预测模型,使得所提出的模型具有更为广泛的适用性,为水资源合理分配提供科学的参考和依据。
[1] LiYP,HuangGH.2006.Aninexacttwo-stagemixedinteger linearprogrammingmethodforsolidwastemanagementin theCityofRegina[J].JournalofEnvironmentalManagement,81:188-209.
[2]ImranM,HuangGH,HuangYF,etal.2005.Aninterval -parametertwo-stageoptimizationmodelforstochastic planningofwaterresourcessystems[J].StochEnvironRes RiskAssess,19(19):125-133.
[3]FuDianzheng,LiYongping,CuoheHuang.2013.Afactorialbaseddynamicanalysismethodforreservoiroperation underfuzzy-stochasticuncertainties[J].WaterResources Management,27:4591-4610.
[4]FuDianzheng,LiYongping,CuoheHuang,etal.2014. DevelopmentofaFuzzy-Markov-BasedIntervalStochastic DynamicProgrammingModelforReservoirOperation Management[J].EnvironmentalEngineeringandManagement Journal,13(3):517-530.
[5]颜凡尘,兰荣华,刘元亮.辽宁省辽河流域水功能区纳污能力分析[J]. 东北水利水电,2006(07):54-55.
[6]HuangGH,LoucksDP.2000.AnInexactTwo-StageStochasticProgrammingModelforWaterResources ManagementunderUncertainty[J].CivilEngineering andEnvironmentalSystems,17:95-118.
TV213.4
A
1002-0624( 2014)06-0033-03
2014-02-12

