基于小波变换的水电机组振动故障分析和特征提取

冯源，葛新峰，潘天航，郑源

(1.云南电网公司电力研究院，昆明 650217；2.河海大学能源与电气学院，南京 210098)

特约稿件

基于小波变换的水电机组振动故障分析和特征提取

冯源1，葛新峰2，潘天航2，郑源2

(1.云南电网公司电力研究院，昆明 650217；2.河海大学能源与电气学院，南京 210098)

通过小波变换的手段对国内某水轮机组的振动异常进行故障分析，详细的阐明了小波奇异性检测的原理以及小波基函数选择的要求。采用Mallat算法，选用Db4小波在多分辨分析下对机组摆度信号进行处理成功提取出故障点的位置，并结合不同的频率分析出机械因素和水力因素造成故障的原因。最后运用连续小波变换的模极大值与尺度的对数关系进行图像拟合，计算出奇异点的Lipschitz指数，以此作为故障信号的特征。通过比较两种不同因素影响的奇异点处的Lipschitz指数，证明其作为故障信号的特征参数对衡量机组故障程度有指导意义。

水轮机组；小波分析；故障分析；Lipschitz指数；特征提取

0 前言

水电站的规模和水轮发电机组的容量越来越大，保证水电机组的安全运行是水电站的首要任务，传统的定期检修方式已经逐渐满足不了高效和准确的要求。近年来状态检修模式正逐渐替代传统的按时检修模式，这种检修方式更加安全可靠但也对状态监测和故障诊断的手段有了更高的要求。水轮机组工作环境复杂，振动受到水力、机械、电磁等因素联合影响，通常在故障出现初期，在振动摆度幅值上很难表现出来，通过常规的在线监测系统根本无法及时发现碰磨故障。

小波分析能够在多尺度分解的情况下同时反映时域和频域的信息，这使得小波分析从频域分析出故障特征时还能在时域给出精确的位置，这种时频结合优越性是传统频域分析法所不具备的。因此近几年来小波分析理论在工程应用的领域中得到极大的发展也在水电机组故障诊断中被越来越广泛地应用。在文中，结合国内某电站的水导轴承摆度信号用小波奇异性分析的方法，准确分析了故障原因并计算出Lipschitz指数，以此作为特征参数的意义。在水轮机组信号处理中目前还没有相关研究出现。

1 小波变换与信号奇异性

1.1 小波变换和分解算法[1]

小波基函数表示为ψa，τa为伸缩因子，τ为平移因子。

小波变换是将信号在小波基函数上进行投影，数学表达如式1所示：

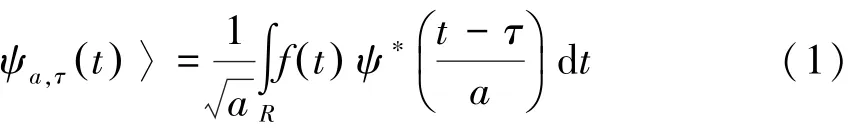
WTa，τ( )=〈f t()，

WTfa，τ( )为小波变换系数。

在线性空间L R()2中，函数f t()，其频谱为f ω()，实际信号的频谱总是有限的，可以选择足够大的m使得f t()∈Vm+1，则f t()可以用Vm+1空间中的标准正交基来表示即

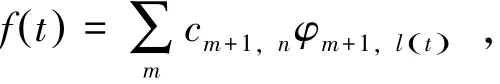
其中cm+1，n=〈f，φm+1，n〉。Mallat算法通过下一级空间Vm+1中的系数Cm+1，k时，来对上一级子空间Vm和Wm中的系数cm，k和dm，k进行计算。以此类推，如图1所示。

图1 Mallat分解算法示意图

1.2 信号的奇异性

当机组运行发生故障时，则在测试信号上往往会表现出奇异性。信号的奇异性表现为两种[2]，一种是幅值上出现明显的突变或不连续，另一种是信号的高阶导数时间断的，尽管这种类型的信号时域上表现光滑，在小波域则表现出有很强的奇异性。

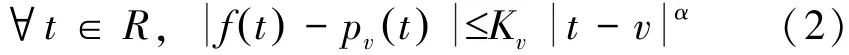
如果存在常数Kv＞0和m次多项式pv(m为小于α的最大整数)使得式 (2)成立称函数f在点v∈R为Lipschitz α(α≥0)。如果与v无关的正数K使式 (2)成立，则函数f在区间 a，b[ ]上是一致Lipschitz α≥0的，Lipschitz α中所有α的最大值称为f t()在v点的Lipschitz指数。式2中Pvt()是f t()在v点的泰勒展开级数的前m+1项构成的多项式，即：

其中，fk()v()表示f t()在v点的k阶导数。

2 故障点的定位

2.1 小波奇异性分析原理

选择不同波形、支撑长度的小波分析结果是有差异的[3-5]。因此，利用小波变换进行信号奇异点检测存在小波基的选择问题。

则称ψ x()具有m阶消失矩。

如果函数如果函数R t()在t0点不可导，在其它点可导，则表示t0为f t()的奇异点。M+l阶的双正交小波φMt()具有M阶消失矩，一个函数f t()∈CN+a(N为整数，a＜1)而言，具有N阶导数，将f t()用泰勒公式展开并进行小波变换得：

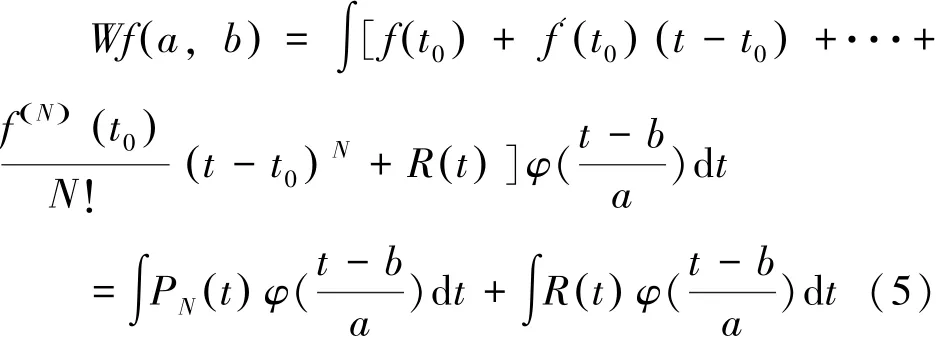
由以上推导可以看出对于导数有限的函数而言，选择小波消失矩大于函数可导的阶数即M＞N，可以使函数在奇异点的领域内小波变换为非零，在远离奇异点的地方变换结果为零，因而可以确定奇异点的位置。相反，如果小波的选择是不合适的，于是式 (5)的第一项不为零，意味着将在远离奇异点的地方也不为零，因而无法定位奇异点。

2.2 仿真分析

用Matlab仿真一个出一个有2阶导数的光滑信号f t()，由于导数不连续在500点出有强奇异性，如式 (6)。分别用Db1、Db2和Db3小波分解式构造的函数 f t()结果如图 2所示。由于f t()具有2阶导数，而Db1和Db2小波的消失矩分别为1和2，所以小波分解的细节系数在远离奇异点500的位置也不为零，无法精确定位出奇异点。Db3小波对函数f t()进行3层分解只在奇异点处系数不为零，其他地方都为零，所以能够很好的定位奇异点。仿真结果也表明只有小波基的消失矩大于信号导数阶数才能成功检测出奇异点。

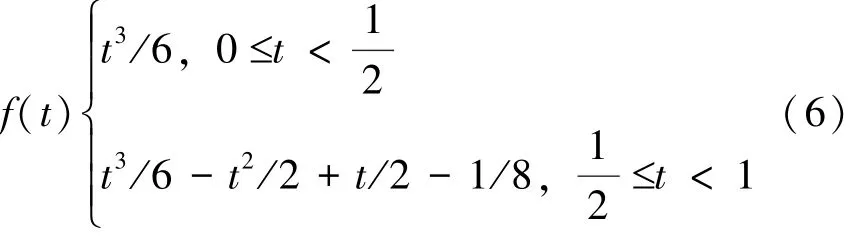
图2 函数f t()图像Db1、Db2、Db3小波分解系数

2.3 实例分析

该水轮机组的转速为136.4 r/min，即转频为2.273 Hz，信号的采样频率为500 Hz。选用Db4小波对水导轴承的摆度信号进行4层分解，原信号和分解细节系数d1～d4如图3所示。

从高频细节 d1看出在点 70、190、290、410、510、630、730、850、950处发生明显畸变，从低频细节d3和d4只有在70、290、510、730、950的采样点奇异性很强。说明这些奇异点是机组运行中不同原因造成的，结合发生频率可将故障的振动频率范围提取出来。采样频率为500 Hz，所以适合研究250 Hz以下的信号。由多分辨分析，细节系数d1频率集中在125～250 Hz，细节系数d4集中在16～31 Hz之间。水轮机组振动故障通常由机械部分、水力部分和电气部分的联合影响所造成，本文研究的水导轴承处的故障主要考虑机械因素和水力因素。经过研究[6]机械因素和水力因素造成振动故障的原因及其频率如表1所示。

由表1看出，机械因素引起的振动频率一般为转频的整数倍，表现为低频，所以频率集中在16～31 Hz细节系数d4所反映的故障点70、290、510、730、950是由机械因素造成的。经过现场检修发现是主轴的碰磨所引起的振动信号的突变，这些故障点周期都是220，换算成时间约是0.43 s，即每转一圈，主轴摩擦一次。而频率主要集中在125～250 Hz的细节系数d1所反映的点190、410、630、850处的奇异性主要是由于卡门涡在绕流体后部产生交变激振力，引起绕流体周期的振动。可以进一步检测，在190起始点处，如果每次振动时间较短且很快恢复，则此处水力因素引起的信号异常可不列为故障。主轴的碰磨故障已经在时域信号中表现的非常明显，需要尽快维修。

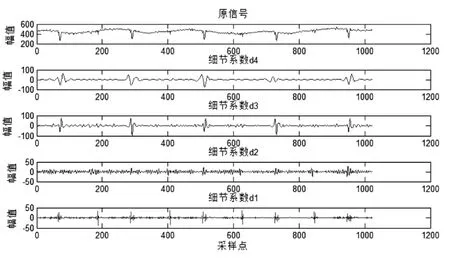
图3 水导轴承去噪后的摆度信号和小波分解系数

表1 振动故障的机械和水力因素及频率

3 奇异性特征指数的提取

3.1特征提取算法

Mallet等人证明[7]：在f t()的某个区间内，如果收敛于v的所有模极大点都包含在锥≤Cs中，函数f t()在v点Lipchitz α，当且仅当存在常数A＞0，使得模极大值点(s，u)满足

即

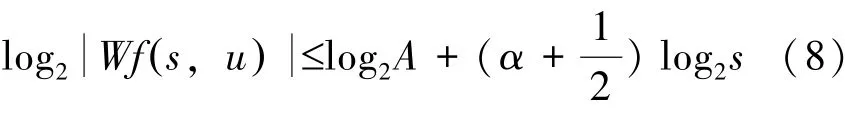
由此可以给出Lipschitz指数的算法：

1)选取适当的阀值对信号去噪。

2)计算连续小波变换。

3)计算小波变换的模极大曲线。Wf( s ，ui)表示信号在s尺度下ui点的小波系数，若在s尺度下ui为局部模极大值点，则满足：

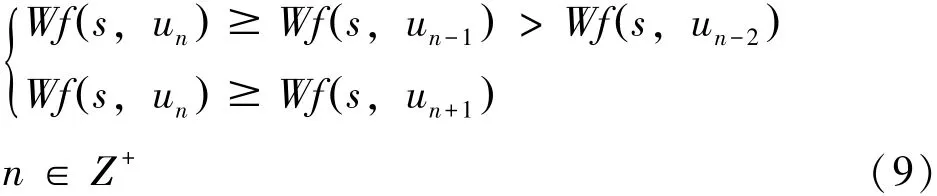
4)选择收敛于v的斜率最大的极大曲线，作出log2与log2s的图像，此斜率的值减去1/2得到Lipschitz指数。

3.2 实例分析

对去噪后的水导轴承摆度信号用Db4小波进行连续小波变换，分析尺度最大为64，连续小波变换的系数和局部模极大值线如图4所示。分别找到奇异点70、290、510、730、950和奇异点190、410、630、850处的模极大值衰减线，作出其log2、log2s()图像。由于篇幅制，且奇异点具有周期性，只给出奇异点70和190处的拟合图像，如图6。

图4 信号的连续小波系数 (上图)和局部模极大值线(下图)

由图5可以计算出70处拟合图像的斜率分别约为1.029，所以奇异点70处的Lipschitz指数α为0.529；奇异点190处拟合图像的斜率分别约为1.203，所以奇异点190处的Lipschitz指数α为0.703。同理求出290、510、730和950奇异点处的Lipschitz指数α分别为0.488、0.513、0.558和0.509，奇异点410、630和850处的Lipschitz指数α分别为0.719、0.745和0.701。

图5 70处 (左图)和190(右图)处李氏指数拟合

研究表明[8-9]，α与信号的奇异性成负相关。通常当α小于1时，认为信号是有奇异性的。因为以上奇异点都是有周期性的，在同一个地方产生故障，故由同一种因素造成的奇异性是差不多的，反映在Lipschitz指数上也是基本相等的。而由不同因素造成的奇异性则是明显不同的，Lipschitz指数也相差较大。碰磨造成信号奇异的α约为0.5，故奇异性较大，所以在时域信号中就发生突变。水力因素造成信号奇异的α约为0.7，故奇异性较小，在时域信号中突变很不明显，但通过小波变换即可以检测到。综上所述，Lipschitz指数的大小可以表征机组故障的程度。

4 结束语

1)理论推导了小波域突变来表示信号奇异点的原因以及小波变换时对小波基选择的要求，基小波基的消失矩要大于信号导数的阶数。通过Matlab信号仿真，证明了上述的推导。

2)用Db4小波对国内某水轮机组水导轴承的摆度信号进行4层分解，结合多分辨分析发现在不同的频率范围内是不同的原因造成机组的振动异常。频率集中在16～31 Hz内的奇异点是由于主轴的摩擦造成，而频率在125～250 Hz内的奇异点主要是由于卡门涡交引起绕流体周期的振动造成的。

3)通过模极大值衰减理论和图像拟合的方法求出信号奇异点的Lipschitz指数，并依此作为机组运行的特征参数。通过分析该机组摆度信号，求出碰磨故障时Lipschitz约为0.5，卡门涡水力脉动引起振动异常的Lipschitz指数约为0.7。表明将Lipschitz指数α作为故障信号的特征参数对衡量机组故障程度有指导意义。

[1] 刘涛，曾祥利，曾军.使用小波分析入门 [M].北京：国防工业出版社，2006.

[2] 孙延奎.小波分析及其应用 [M].北京：机械工业出版社，2005.

[3] 王旭慧，江琦.小波分析在汽轮机振动故障诊断中的应用研究 [J].电力学报，2014，29(1)：80-83.

[4] 王绥瑜，邢铀，蔡渊.基于小波分析的变压器在线故障诊断探究 [J].电子测试，2014，1：4-9.

[5] 胡晶，范铮.小波算法在旋转机械故障诊断系统中的应用[J].工业仪表与自动化装置，2014，1：46-50.

[6] 梁武科，张彦宁，罗兴绮.水电机组故障诊断系统信号特征的提取 [J].大电机技术，2005，4：53-56.

[7] Stephane Mallat，Wenliang Hwang.Singularity Delection and Procession with Wavelet[R]， Courant Institute of Mathematical Science，New York University，1992.

[8] 郑源，张飞.基于连续小波变换的泵机组主轴径向摆度信号处理 [J].2009年全国大型泵站更新改造研讨暨新技术、新产品交流大会论文集.

[9] 王东，丁宣浩，陈利霞.信号奇异性的Lipschitz意义 [J].桂林电子工业学院学报，2003，23(5)：9-12.

Research on Vibration Fault Diagnosis and Feature Extraction of Hydraulic Turbine based on Singularity Detection with Wavelet

FENG Yuan1，GE Xinfeng2，PAN Tianhang2，ZHENG Yuan2
(1.Yunnan Electric Power Research Institute，Kunming 650217，China；2.School of Energy and Electric，Hohai University，Nanjing 210098，China)

By means of wavelet transform to analyze the abnormal vibration of domestic turbine units and combining theoretical derivation and Matlab simulation to illustrates the principle of wavelet singularity detection and the requirements of selecting wavelet basis function.Under the multi-resolution analysis，using Db4 wavelet to decompose the shaft vibration signal with the algorithm of Mallat and in different frequency range，the analysis shows that the causes of abnormal vibration are mechanical and hydraulic factors.Finally，make the image of modulus maxima of wavelet continuous transform and scale's logarithmic relationship to calculate the Lipschitz index of singular points，which is as the characteristic of the fault signal.Comparing the Lipschitz index of singular points caused by two different factors，it proves that as a fault signal's characteristic parameters，the Lipschitz index has a guiding significance to measure unit fault degree.

hydraulic turbine unit；wavelet analysis；vibration fault diagnosis；Lipschitz index；feature extraction

TV73

B

1006-7345(2014)06-0001-04

2014-06-06

冯源 (1983)，男，硕士，工程师，云南电网公司电力研究院，研究方向为水电机组状态监测和故障诊断 (e-mail) fengyuan1678＠163.com。

云南电网公司科技项目 (K-YN2012-452)和江苏省博士后基金 (1102072c)