尾气静电传感器空间灵敏度有限元仿真研究

白　杰，孙　伟，吴延松，王　伟

(中国民航大学民用航空器适航与维修重点实验室，天津　300300)

0　引言

发动机故障在飞机故障中占相当大比例，而气路部件故障占发动机故障的90%以上。航空发动机在不同的工作状态下会产生浓度、大小不同的碳烟颗粒；而发动机吸入外物会造成损伤，产生颗粒物；另外当发动机发生故障时，如叶片烧蚀、涂层剥落、叶片与机匣间的碰摩等都是尾气中异常颗粒物的可能来源。基于气路颗粒荷电信息的航空发动机尾气静电监测是一项新的监测技术，它是根据发动机尾气中电荷量的变化来实现对气路部件状态的监测，从而获得发动机的工作状态和健康状况[1]。

航空发动机尾气静电检测技术的核心元件是尾气静电传感器。静电传感器主要分为环状和棒状两种，由于环状的传感器对中心区域的颗粒不敏感，只适合于管道口径较小的环境中，因此面对航空发动机这一大管径输送系统采用棒状传感器。传感性能的优劣直接影响系统的准确性和快速性。衡量传感器的优劣以及检验和使用传感器的依据是其性能指标，判断传感器的好坏可以通过建模来实现。目前，国际上对静电传感器数学模型的研究几乎均建立在大量假设条件的基础上，进而实现机理建模，如Gajeski模型[2]、Yan模型[3]、Mumane模型[4]等，但这些模型建立过程中存在着较多的假设条件，要获取解析结果较困难。有限元法在数值计算中应用广泛，为解决复杂的分析计算与设计提供了有效的途径。文中首先建立点电荷在静电传感器灵敏空间的数学模型，然后采用ANSYS有限元分析软件对静电传感器敏感元件建立有限元模型，对不同几何形状的尾气静电传感器空间静电场进行数值分析，进而获得传感器空间灵敏度分布情况。

1　尾气静电传感器数学模型

当带点颗粒经过测量电极时，会在电极的近段和远端产生大小相等、正负相反的电荷，感应电荷量的大小是所有带点颗粒产生的感应电荷总和。这里可以把带点颗粒当作点电荷，点电荷所产生的静电场与电极上感应电荷相互作用，导体达到静电平衡，此过程在极短的时间内完成(10-19s)，因此，移动点电荷与静电传感器之间的相互作用可以用静电场来描述。点电荷在传感区域内，静电场满足以下泊松(Poisson)方程和狄利克雷(Dirichlet)边界条件：

·(φ)=ρ/ε0

(1)

φ(Γe)=0∪φ(Γf)=0∪φ(Γn)=0

(2)

式中：φ为场域内电势；ρ为场域内体电荷密度；ε0为空气介电常数；Γe、Γf、Γn分别是管线、绝缘层、电极构成的边界。

上式求解得到空间电势后，由高斯定理可以得到电极上的感应电荷密度。电极为导体，是一个等势体，其表面的电场强度沿着导体变面的法线方向，感应电荷面密度表示为：

σ=B=ε0E=-ε0·φ

(3)

式中：σ为电极上感应电荷密度；B为电极表面的电位移矢量；E为电极表面的电场强度。

将感应出与施感电荷异号的电荷，而在接地外壳包围的部分可以看成是远端，主要感应出同号电荷。因此，在这里对电极近端的外表面s的感应电量Q，可以通过下式获得：

(4)

上述的数学模型可以看出电传感器数学模型的边界条件较为复杂，要获得上述数学模型的解析较为困难，一般采用数值求解的办法实现上述感应电量的计算过程。因此选用ANSYS有限元法分析软件对静电传感器的传感特性进行仿真分析[5]。

2　建立有限元模型

选择静电传感器的轴向作为整体坐标系的z轴，径向作为x轴，切向作为y轴。静电传感器的电极是一个圆柱形导体，灵敏度与电荷到探极表面的距离有关，根据对称性，选取探极的中心轴为轴线，荷电颗粒到感应探极的距离是绕轴线旋转对称的，因此可以把点电荷所形成静电场简化为二维静电场，从而简化了模型。单位点电荷在任一位置上，其在电极上的感应电量均可求得。

进行二维静电场有限元分析，根基结构形状和精度要求选取8节点2-D四边形或三角形轴对称单元PLANE121。通过以下参数建立有限元模型：电极的半径R、轴向长度L和电阻率；绝缘介质的厚度D和相对介电常数εr；施加电荷载荷的空气域长度Kl、宽度Kw和相对介电常数ε0；电极在空气域部分L1、在传感器外壳中部分L2、电极下端面距离空气域底端为LH．图1为有限元网格划分图，由于电极附近电势变化剧烈，为了精确计算结果，所以网格进行局部细化。电极为导电性良好的镍基合金，各点电势相等，因此不需要进行网格划分，只需将电极边界节点自由度进行耦合使其电势相等[6]。

图1　静电传感器有限元网格划分图

对模型施加边界载荷，将传感器外壳和管线设置为零电压。电荷是集中载荷类型，在空气划分的网格节点上施加电荷作为载荷。利用ANSYS波前求解器直接求解即可精确获得结果。AYSYS求解获得的是节点电势。下一步分析的需要求得电极上的感应电量。因此需要对计算结果进行后处理，利用式(3)和式(4)即可获得电极上的感应电量。

3　尾气静电传感器空间灵敏度分析

灵敏度特性是反映静电传感器感应性能的一个重要参数。静电传感器空间灵敏度定义为：在敏感空间某一位置上，单位点电荷作用下，电极上感应电量的绝对值。静电传感器敏感元件的灵敏场分布在一个较大的三维空间中，灵敏度分布受到静电传感器的结构尺寸和材料属性等因素的影响。静电传感器有限元分析模型可知，点电荷在敏感空间某一位置上，电极上的感应电量仅仅与点电荷距离电极表面的径向坐标x和沿着电极的轴向坐标z有关，所以静电传感器敏感元件空间灵敏度可表示为：

s(x，z)=|Q/q|

(5)

式中：q为施感的点电荷；Q为在点电荷q作用下，电极上的感应电量。

因此，改变点电荷在空间的位置，通过上述有限元模型分析，即可获得特定结构静电传感器的灵敏度空间分布特性。

模型中首先设定半径为5 mm，绝缘介质厚度为D=10 mm，相对介电常数为2.25。在6个不同位置(x，z)施加不同电量的施感电荷，分析感应电荷大小随施感电荷大小变化情况，由图2可以看出，感应电荷大小随施感电荷大小线性增加，其斜率即为传感器在该点的灵敏度，测量点的位置不同，传感器探极在该点处灵敏度也不同。

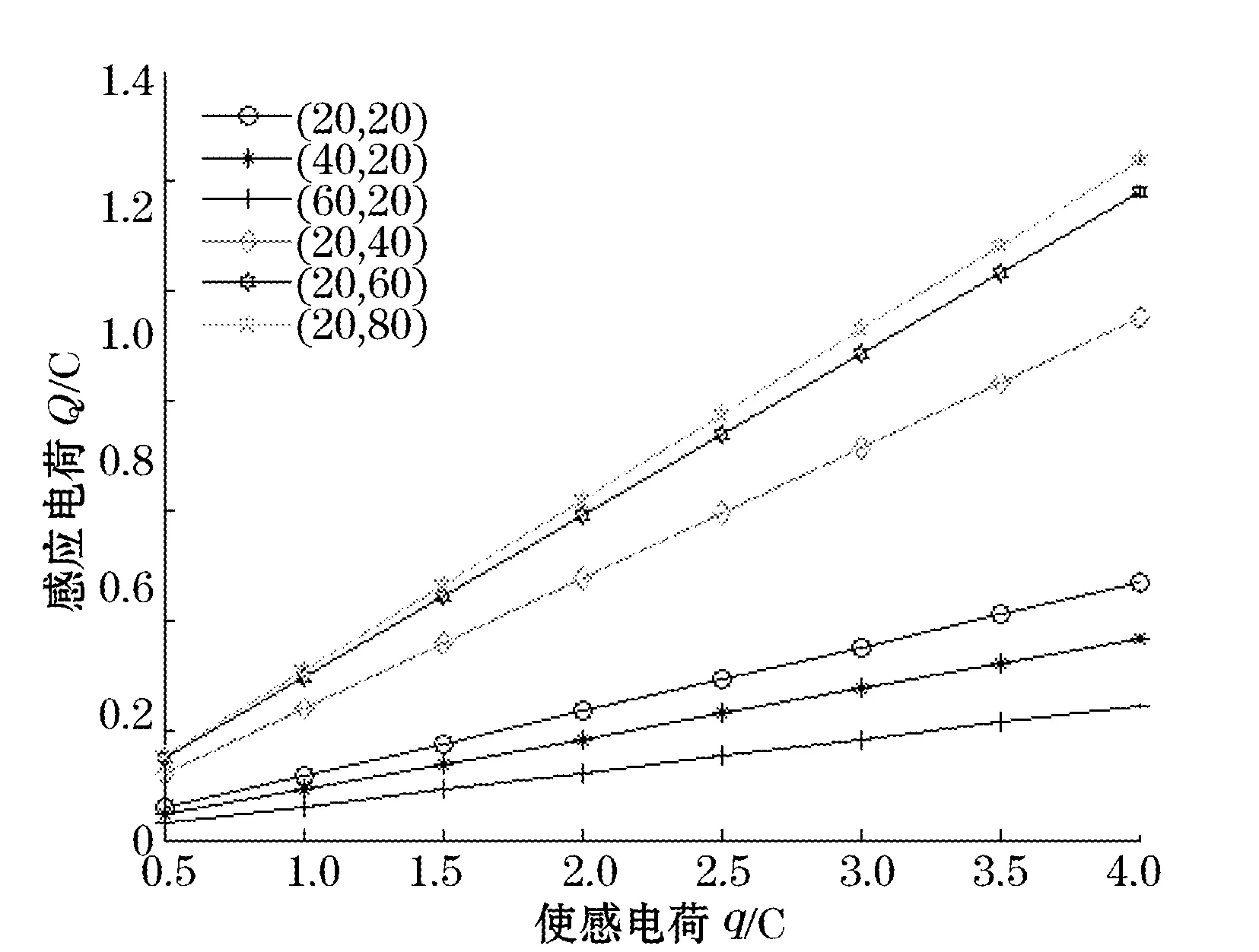
图2　静电传感器感应电荷随使感电荷变化图

为了分析当施感电荷位于探极周围不同位置处时，传感器空间灵敏度变化，设施感电荷为1C，保持一定的轴向坐标z，让点电荷随经向坐标移动，获取静电传感器的空间灵敏特性，如图3所示，可以看出，当轴向位置z一定时，灵敏度s随|x|变大而减小，且随距离电极位置边缘，减缓趋势逐渐减弱，直至衰减到可以忽略。在不同的轴向位置敏感度也不同，如图4所示，为当径向位置x一定时，灵敏度随轴向位置z的变化图。当径向位置x不同时，沿静电传感器轴向位置的空间灵敏度是不同的，当|x|值较小时候，空间灵敏度沿着轴向方向变化比较明显，这是因为电极结构对电极周围附近的灵敏场具有较大影响；随着|x|值的增大，空间灵敏度随轴向位置的变化趋于平缓；随着电极轴向z值的增大，即越靠近传感器探极根部，空间灵敏度变小，其主要原因是静电传感器外壳以及其相连接的管体的影响。

图3　灵敏度随径向位置变换曲线

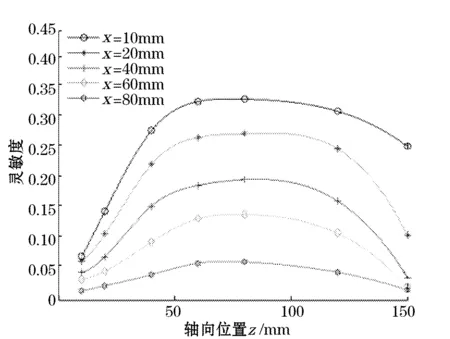
图4　灵敏度随轴向位置变换曲线

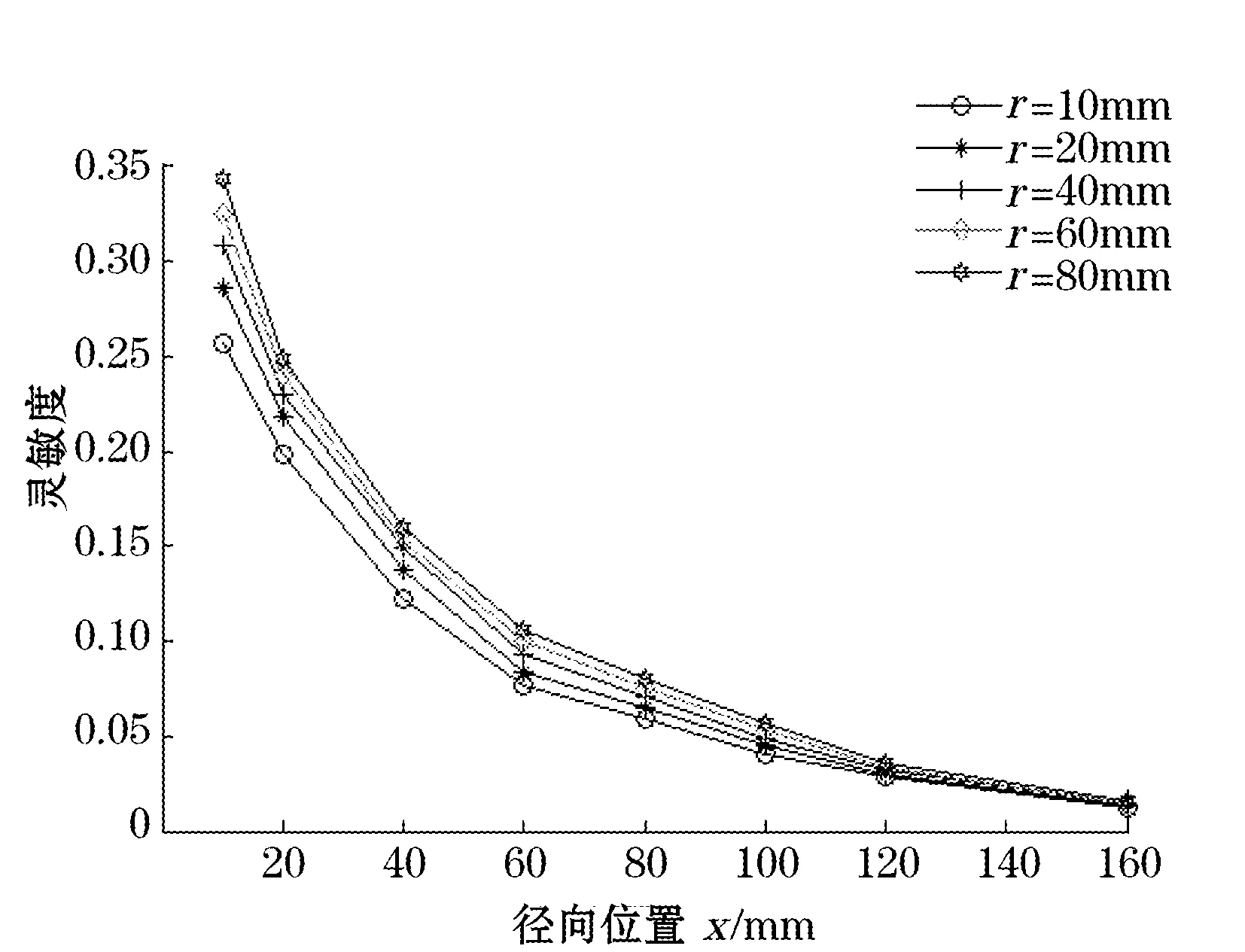
图5　不同径向位置半径对灵敏度的影响

在保证模型的其它参数不变的前提下，依次计算了不同半径(r=1 mm，3 mm，5 mm，7 mm，9 mm)的探极在空间不同位置处的灵敏度。图5为轴向位置相同(z=60 mm)，不同半径的感应探极灵敏度沿着径向位置分布的情况，沿x轴向分布上，随着x的增加，电极半径对静电传感器敏感元件灵敏度的影响逐渐减小。图6为在探极轴向位置z=60 mm处，不同半径的探极在相同的径向位置时的灵敏度比较图，由图可以看出随半径增加灵敏度略有增加，半径对灵敏度影响不大。

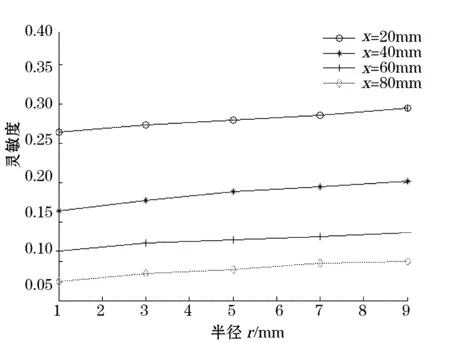
图6　z=60 mm处半径对灵敏度的影响

考虑到尾气静电传感器的实际用途，需要将静电传感器安装于高温的航空发动机尾气中，由于静电传感器探级与放大电路连接，考虑到连接引线过长导致的信号失真，需要将放大电路与探级设计为一体，因此需要耐高温的绝缘材料包裹部分电极和放大电路，并与传感器外壳进行隔离。在静电场的作用下，绝缘介质发生极化，形成束缚电荷，从而影响静电传感器敏感空间电场分布和传感器的空间灵敏度。下面就绝缘介质的介电常数和绝缘介质厚度对传感器的空间灵敏度的影响进行分析。

保证其他相关参数不变，依次计算了不同介电常数(εr=1、2.55、3.75、6、10)时探极在空间不同位置处的灵敏度。图7为同一半径的探极，在轴向位置为z=40 mm时，在不同径向空间内，介电常数对灵敏度分布的影响，从图中可以看出，随着介电常数的增加，灵敏度有所增加。图8为同一半径的探极，在同一径向空间内，在不同轴向距离，介电常数对灵敏度大小的影响。综合图7和图8来看，说明介电常数增加，其灵敏度值均会略有增加，且变化幅度随介电常数的增加而减小。

图7　不同径向位置灵敏度随介电常数的变化曲线

图8　不同轴向位置灵敏度随介电常数变化曲线

保证其他相关参数不变，依次计算了不同介质厚度(D=5 mm、10 mm、15 mm、20 mm)时探极在空间不同位置处的灵敏度。图9为不同厚度的绝缘层，灵敏度沿径向x的分布曲线。图10为不同厚度的绝缘层，灵敏度沿轴向z的分布曲线。由图可见，起初随着绝缘层厚度的增加，静电传感器敏感元件灵敏度下降较为明显，但随着绝缘层厚度的增加，其下降趋于缓和。因此，绝缘层厚度的增加，静电传感器敏感元件灵敏度空间分布更为均匀，但导致了灵敏度的降低。

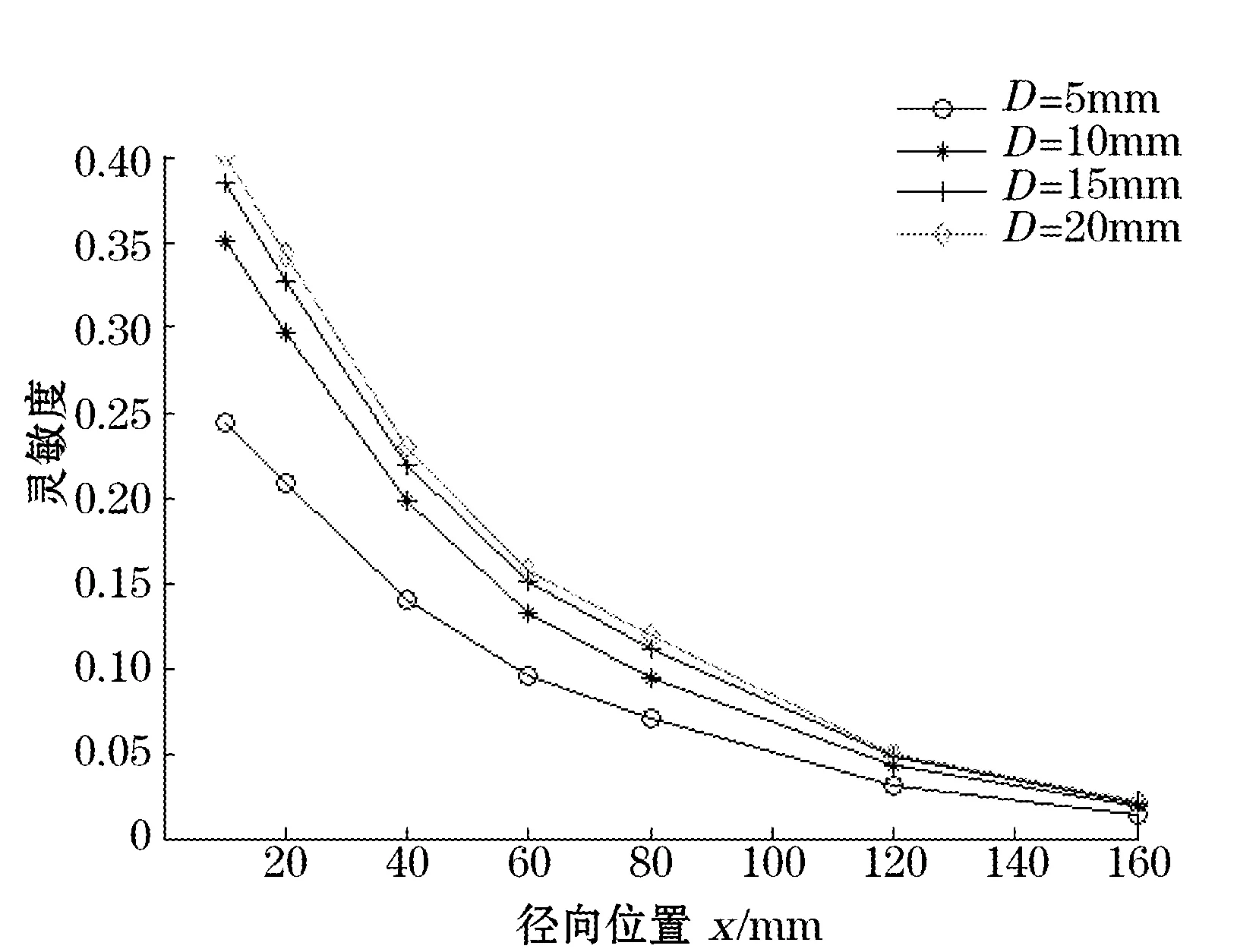
图9　厚度对径向灵敏度分布的影响

图10　厚度对轴向灵敏度分布的影响

4　结论

增加传感器半径对增加灵敏度空间的大小影响不大，但在一定径向距离范围内，探极半径大的传感器灵敏度高。但是探级半径过大，将阻碍尾气的排放，影响发动机的正常运行；探极半径过小，传感器空间灵敏度降低，并且探极输出电量变小，信噪比降低，检测难度增加。绝缘材料选用介电常数为2.55和3.75，分别对应着聚四氟乙烯和陶瓷，尽管增加绝缘材料的厚度，可以增加探极的灵敏度空间，但势必造成传感器的体积增大许多，况且为了根据传感器设计的空间需求，绝缘材料陶瓷的厚度也要根据需求做适当调整。所采用的绝缘材料的介电常数和厚度对灵敏度分布都有着类似的影响。文中的计算结果忽略了部分影响因素，仅为理论结果，在实际工程应用中，还需要考虑传感器实际设计时候的空间、装配以及传感器所处高温环境因素的影响。在进行实际运用时，还需要多次进行发动机台架试验，对测试数据反复分析论证，不断修改传感器尺寸参数，以确保传感器满足使用要求，并且具有较高的性价比。

参考文献：

[1]马敏，张钊，侯敏，等．航空发动机气路监测系统静电传感器仿真研究．河南科学，2013，31(3)：307-313．

[2]GAJEWSKI J B．Mathematical model of non-contact measurements of charges while moving．Journal of Electrostatics，1984，15(1)：81-92．

[3]YANY，BARNES R N，WOODHEAD S，et al．Velocity measurement of pneumatically conveyed solids using electrodynamic sensors．Mea．Sci．Technol，1995(6)：515-537．

[4]MURNANE S N，BARNES R N，WOODHEAD S R，et al．Electrostatic modeling and measurement of airborne particles concentration．Proc．IEEE Conf．Instrumentation and Measurement Technology，1995：762-765．

[5]许传龙，王式民，孔明，等．静电传感器空间灵敏度特性研究．计量学报，2006，27(4)：335-338．

[6]文振华．基于静电感应的航空发动机气路监测技术研究．南京：南京航空航天大学，2009．