利用伪随机斩波技术的微弱MEMS信号检测电路

何　鑫，王玮冰，祖秋艳，宋冬雪，孙业超

(1．中国科学院微电子研究所，中国科学院微电子器件与集成技术重点实验室，北京　100029；2．江苏物联网研究发展中心，江苏无锡　214135)

0　引言

MEMS传感器前端读出电路因为其具有高线性度、电路结构简单和温度系数小等优点，正受到更多的关注和研究。然而MEMS前端读出电路位于处理电路中引入噪声和失调的重要位置，这些噪声和失调必须通过电路处理技术将其消除。常用减小噪声和失调的技术有相关双采样[1](CDS)、自稳零技术(auto-zero)和斩波放大技术[2](chopper)等。通过比较，在连续时间放大电路中，斩波放大技术可以更好地减小低频噪声和失调，但是由于调制解调过程中引入了开关尖峰和电荷注入，所以在斩波频率附近产生纹波即残余失调。为了消除残余失调，提出了采用伪随机频率[3]斩波，即利用伪随机频率信号的自相关性[4]，减小剩余的残余失调[5]和残余的波动幅度。

1　伪随机频率斩波检测原理

1．1斩波放大原理

图1为一个传统MEMS斩波放大电路[2]的简图，调制器S1和解调器S2同时受到斩波频率时钟CLK控制，左侧是一个典型的可变MEMS电容电桥电路，中间的运算放大器A1能够将传感器的输出信号进行放大处理，通过解调器S2将失调和噪声调制到高频，最后低通滤波器P1将高频的噪声和失调滤除，被解调器S2解调的低频信号则无衰减地通过低通滤波器P1，得到放大后的传感器信号。

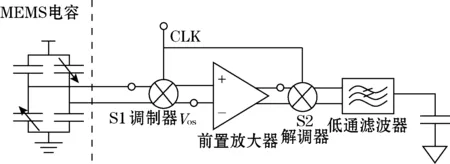
图1　传统MEMS斩波放大电路简图

采用斩波技术后，运算放大器A1中的失调电压VOS被消除，但是调制器S1和解调器S2的开关尖峰和电荷注入效应会产生额外的残余失调电压。在斩波信号CLK的频率比较低的情况下，可以忽略解调器S2的失调贡献，所以等效输入残余失调约为：

Vos，residual≈2Vinjτfchop

式中：Vinj和τ为输入斩波开关的尖峰信号的幅度和时间常数。

过高的斩波频率fchop将引起残余失调电压的显著增加。另一方面，经过解调器S2后，放大器A1的初始失调VOS，static和1/f噪声被调制到斩波频率fchop附近，形成高频波动，不能被低通滤波器P1完全滤除，残余的波动幅度为：

式中：gml为放大器的输入管的跨导；CLP为输出端低通滤波器电容。

1．2伪随机调制自相关性原理

伪随机调制信号[6]是一种周期信号，若观察小于一个周期，其与真随机二进制序列一样，它是一种在一定范围内频率呈现伪随机变化的信号。文中提出的伪随机调制自相关检测原理如图2所示。

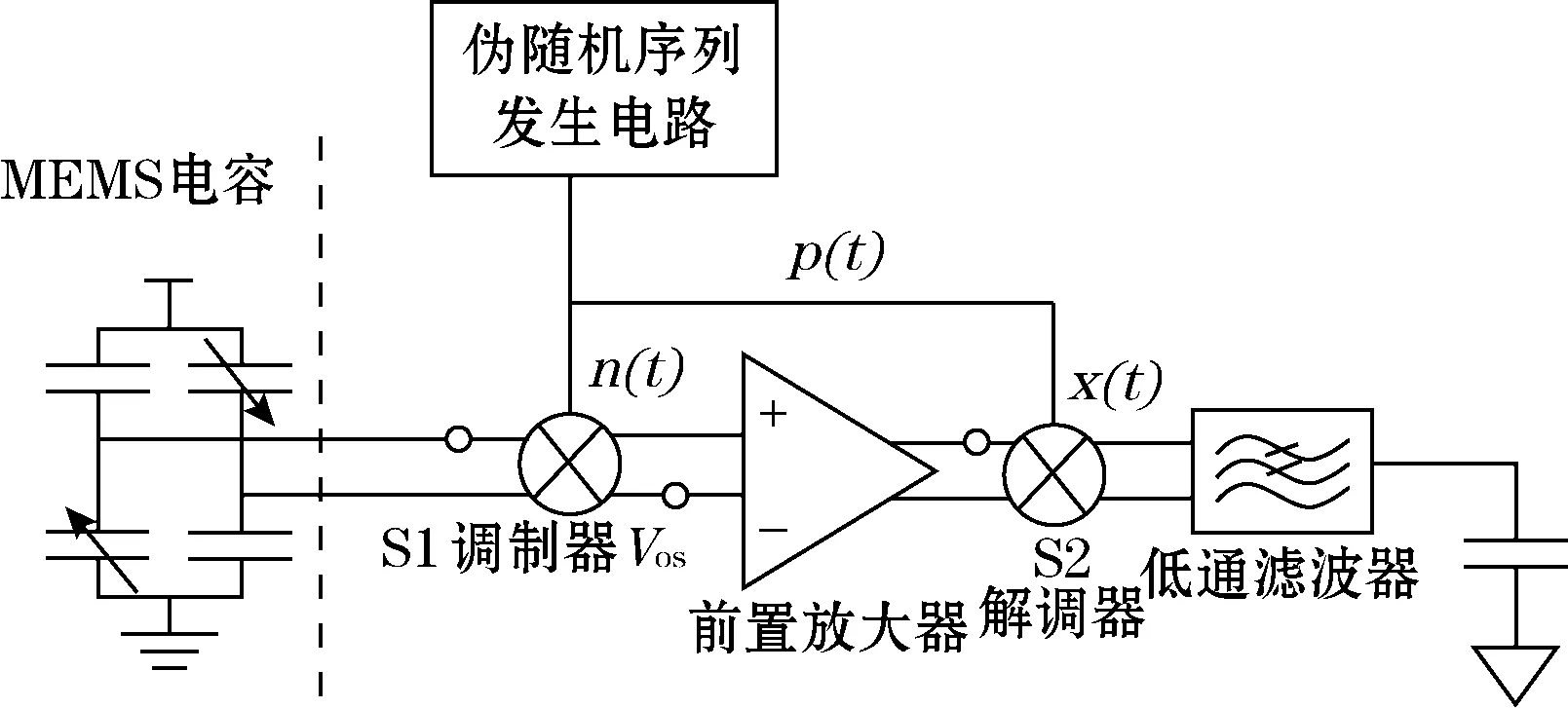
图2　伪随机调制自相关检测电路

前端伪随机序列p(t)由反馈移位寄存器电路产生，用p(t)代替之前斩波放大电路中的斩波频率信号CLK，经过运算放大器A1放大后的信号同时引入了放大器的噪声和失调n(t)，如果用x(t)表示放大器输出的信号，那么有

x(t)=A[s(t)+n′(t)]+n(t)

式中：A为放大器的放大倍数；s(t)为经过调制器S1调制的传感器信号；n′(t)是上一节提到的Vos，residual和Vripple，residual时域序列。

x(t)作为放大器放大后的信号包含了与p(t)相关的信号s(t)和与p(t)不相关的随机的噪声失调信号n(t)和n′(t)，因此，x(t)将同发送端的伪随机序列p(t)进行互相关运算，互相关函数为：

化简为：

ARPP(τ)+Rnp(τ)+ARn′p(τ)

由于信号s(t)是自相关的，所以

Rpp(τ)=δ(τ)

式中δ(τ)为脉冲函数。

而伪随机序列与噪声、干扰不相关，故有Rnp=0和Rn·p=0，从而可以得到总的互相关函数Rxp=aδ(τ)，此互相关式子表示混杂在信号中的失调[7]和噪声[8]以及Vos，residual和Vripple，residual可以通过互相关运算消除。

2　实验仿真

为了验证实验电路的降噪效果，利用软件Cadence Virtuoso/Spectre仿真工具对伪随机斩波放大电路[9]在华润0.5 μmDPTM工艺下进行了设计和仿真。图3为实验电路的版图，面积为430 μm×420 μm．

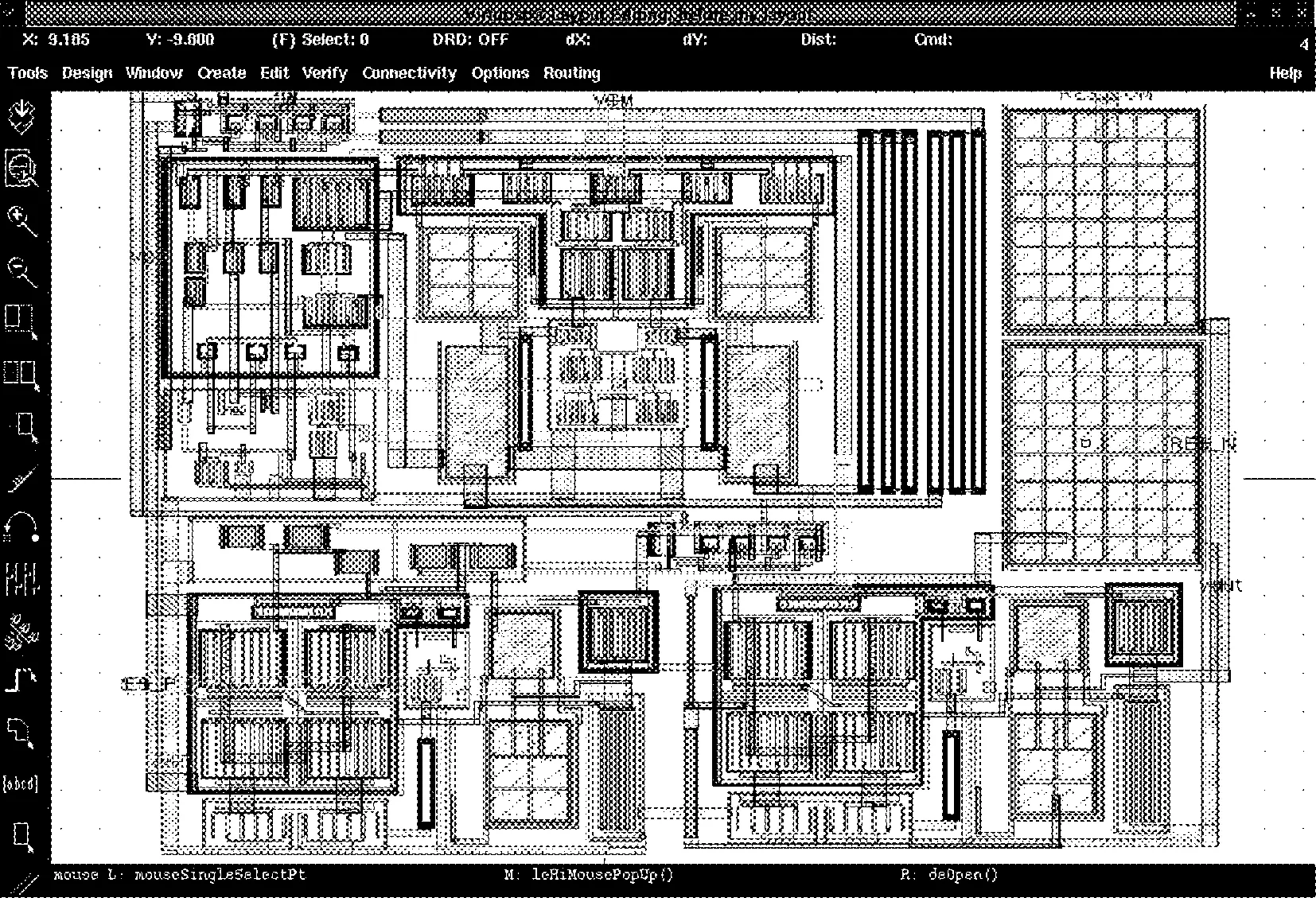
图3　实验电路版图结构

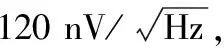
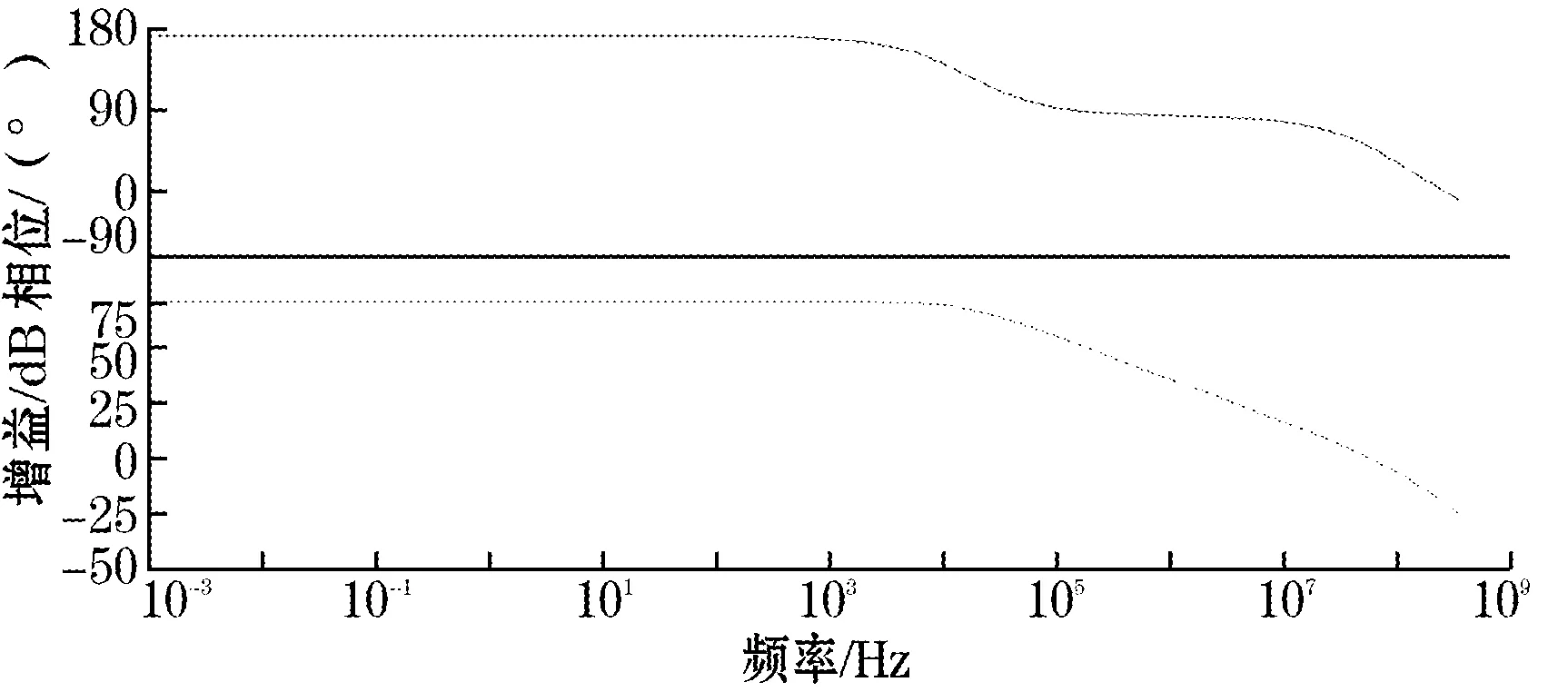
图4　运算放大器的幅频、相频响应

为了验证伪随机频率斩波相关性对噪声的滤除作用，采用了模拟信号阵列模仿伪随机斩波频率，分别取伪随机频率变化个数为n=2，n=4，n=8，n=16，对放大后的信号进行DFT变换，得到图5，分析信号幅值和残余失调的大小，如表1所示，可以看出伪随机频率个数与输出信号之间的关系，即随着伪随机频率变化的个数的增加，对残余失调减小的效果越明显。

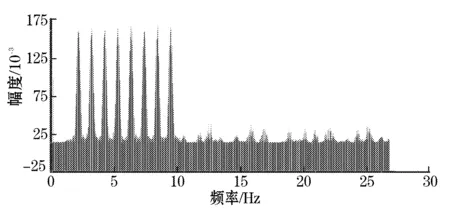
(a)　n=8

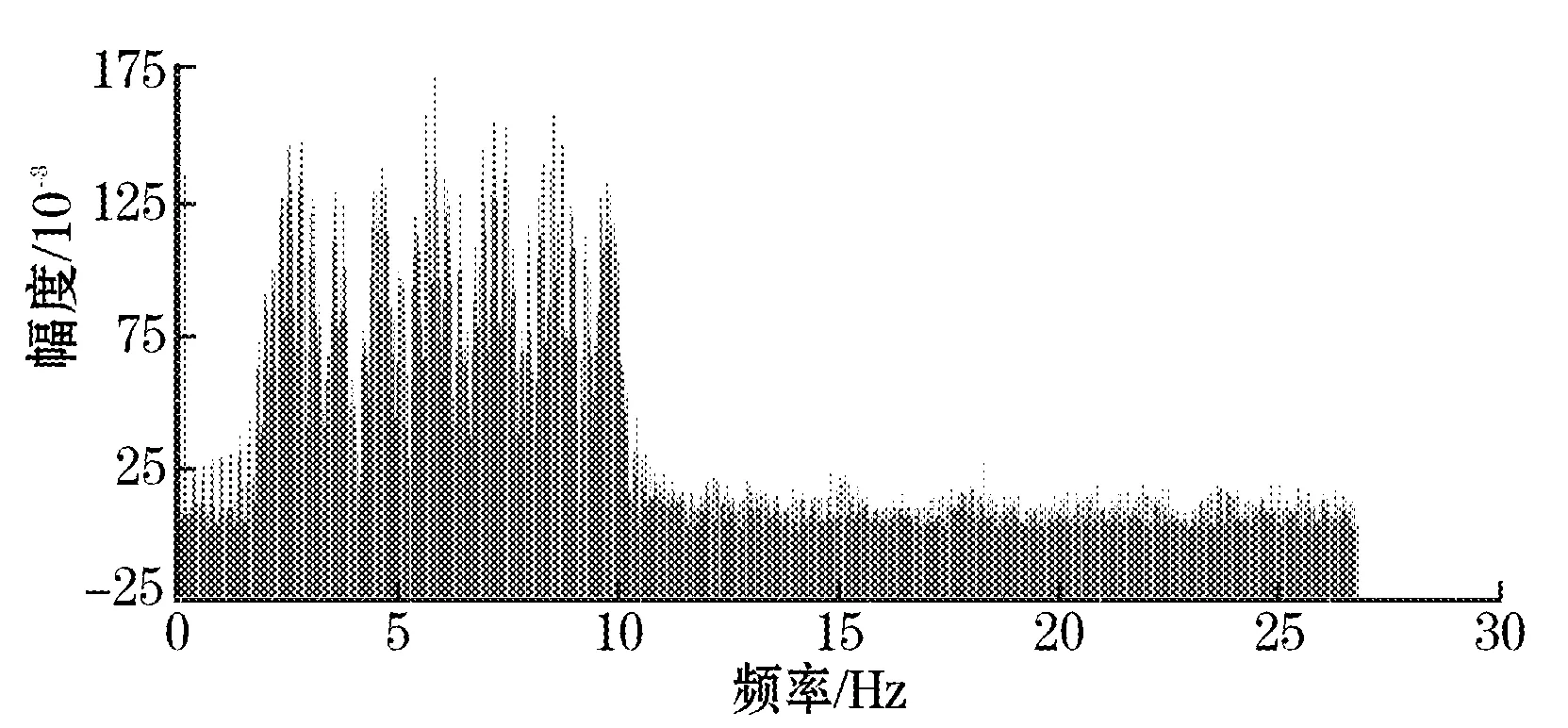
(b)　n=16

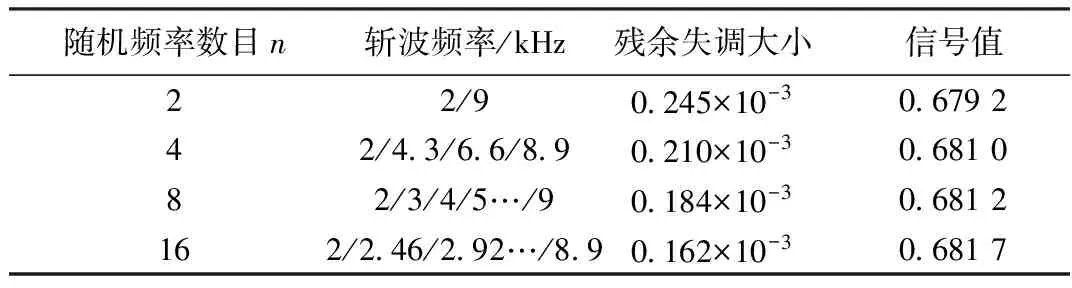
表1　伪随机采样个数与输出残余噪声关系

3　结论

从原理和实验两个角度对随机斩波电路做了解释和分析，通过分析上述的数据和电路可以了解到伪随机频率斩波电路可以降低失调和噪声。如果伪随机频率的个数n更大，将会降低更多的残余失调。表2是对相关双采样、自稳零[10]等技术与该方法进行对比。

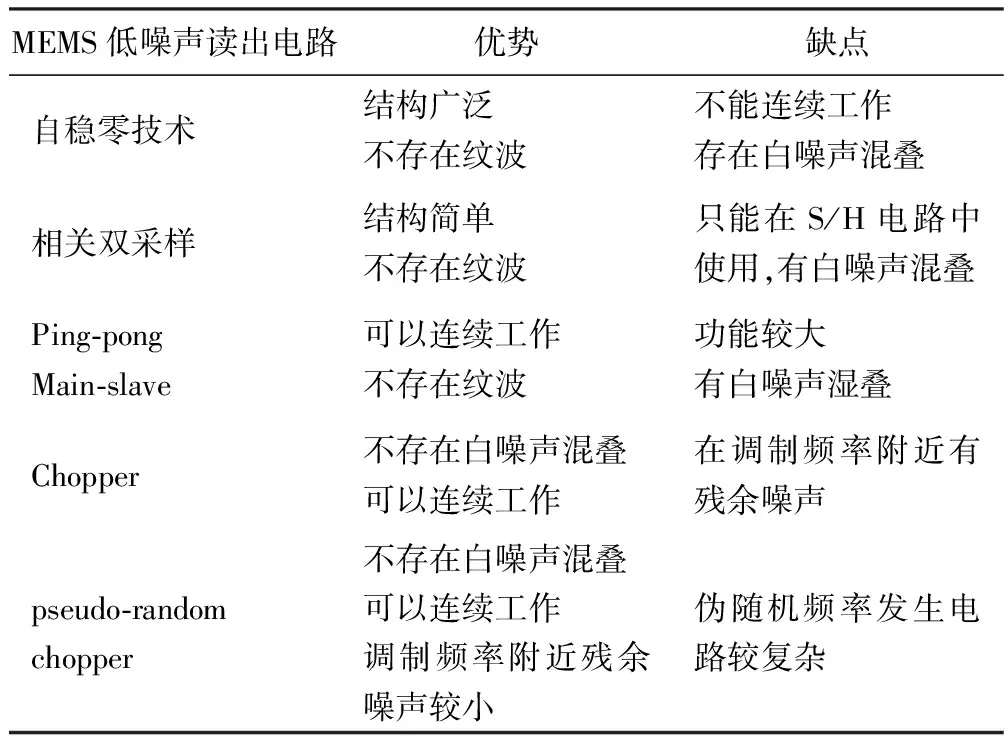
表2　几种降低噪声和失调的方法

由表2可见作为消除环境干扰和噪声的技术，伪随机斩波调制电路适合于MEMS传感器读出电路的设计和研究。

参考文献：

[1]CARUSONE T C，MARTIN D A．Analog integrated circuit design．2012 John Wiley & Sons，2012．

[2]PHILLIP E A，HOLBERG D R．CMOS analog circuit design．2ed．冯军，译．北京：电子工业出版社，2010．

[3]NOJDELOV R，NIHTIANOV S．Capacitive-sensor interface with high accuracy and stability．IEEE Transactions on instrumentation and measurement，2009，58：1633-1640．

[4]高晋占．微弱信号检测．北京：清华大学出版社，2002．

[5]尹韬，杨海刚，刘珂．一种适用于微传感器读出电路的低噪声低失调斩波放大器．半导体学报，2007，28(5)：797-801．

[6]张宝荣，郑德忠，孙长伟，等．基于伪随机序列的微弱光信号检测．电子学报，2009，(9)212-214．

[7]BRRACKE W，PUERS R．Ultra low power capacitive sensor interfaces．Springer，2007．

[8]毕查得·拉扎维．模拟CMOS集成电路设计．陈贵灿，程军等译．西安：西安交通大学出版社，2002．

[9]何鑫，王玮冰．应用于MEMS读出电路的伪随机调制解调斩波电路：中国，201210254637．4．2012．

[10]ENZ C C，TEMES G C．Circuit techniques for reducing the effects of op-amp imperfections：auto-zeroing，correlated double sampling，and chopper stabilization．IEEE，1996，84(11)：1584-1614．