基于亚像素边缘检测的PCR芯片参数测量系统
刘 勇,王卫华,李志刚,张 文,夏营威,孙 淼,张 龙
(中国科学院安徽光学精密机械研究所,安徽合肥 230031)
0 引言
PCR(Polymerase Chain Reaction)芯片是运用MEMS(Micro-Electro-Mechanical Systems)技术在硅片或玻璃片等基片材料上加工的一系列微管道、微反应腔等空间结构,提供了DNA聚合酶链式反应的物质条件。工作时,试剂在管道区间中连续流动实现PCR扩增,对其流速控制具有较高要求。根据流体力学[1]相关理论,对微管道反应腔宽度尺寸的精确测量是流速控制的关键。
该文设计了基于机器视觉的PCR芯片反应腔宽度测量系统。系统获取待测图像后,通过边缘提取算法获得图像待测边缘信息,最后计算出宽度值。但传统边缘检测算法[2-4]如Sobel算子、Robert算子等,虽然易于实现,但是定位精度还停留在整像素级别,已不能满足PCR芯片反应腔测量的需求。为了提高测量精度,决定采用目前较为成熟的亚像素边缘检测算法。
目前亚像素边缘检测算法主要有以下3类:插值法、拟合法和矩方法。相关研究[5-6]表明:插值法运算量小,计算时间短,重复性好,抗干扰能力较强,但定位精度较低;拟合法抗干扰能力强,定位精度较高,但抗干扰能力和检测复杂形状边缘之间存在矛盾;矩方法定位精度较高,但运算量较大,计算时间较长。该文所做的边缘检测是对PCR芯片的管壁图像进行处理,边缘形状简单,综合考虑上述几种方法的优缺点和测量实际情况,决定选用基于拟合法的高斯拟合边缘检测算法。
1 测量系统结构
机器视觉系统通常由照明系统、图像采集系统、图像分析系统等组成。其基本原理是对采集的图像进行形态学处理,通过一定图像处理算法计算出所需数据,这种方法避免了机械式测量所产生的操作误差,特别适合微小几何量测量。该系统以机器视觉系统为基础,由精密测量平台、照明系统、图像模块组成,测量系统结构如图1所示。

图1 系统结构框图
进行测量时,首先将PCR芯片放在载物台上,控制二维电动平台将PCR芯片移动至相机视场中心位置。图像模块采集到芯片图像后用改进的亚像素定位算法提取出图像边缘并计算出待测参数,最后存储并输出测量结果。
1.1精密测量平台
精密测量平台由样品及夹持装置、动力及传动装置、增量式线性编码器及其他位置传感器、运动控制卡所组成的闭环运动控制系统。精密测量平台及其控制系统是整个测量系统的核心,完成多种控制指令和信号处理、传输等任务。控制系统包括2个单片机控制子系统,一个对测量平台的移动进行精确控制,另一个是光栅尺数据采集与处理的控制系统。
1.2照明系统
照明系统是图像测量技术关键部件之一,其主要目的是以合适的方式将光线投射到被测芯片上,突出被测特征部分的对比度。合适的照明系统可使后续的图像处理算法变得简单可靠。该文照明系统包括前场照明光源和后场照明光源。
1.3图像模块
图像模块包括图像采集和图像分析2部分。图像处理研究表明:经过图像采集卡采集的图像,对其特征边缘灰度值求导,所得到的梯度值近似呈高斯曲线分布,高斯曲线的极值点即为边缘点。根据梯度值的这种特点,定位算法首先选用LOG(高斯-拉普拉斯算子)算子对CCD获取的图像进行边缘初步定位,然后在图像边缘粗定位的基础上划定一个窗口,最后对窗口内的边缘像素梯度值用高斯曲面拟合算法进行进一步的精细定位。
2 边缘定位算法分析
2.1像素级边缘定位
像素级边缘定位的目的是通过使用单像素级别的边缘检测算法,对图像边缘目标进行初步定位,从而获得单个像素的定位精度。
LOG算子相对传统的边缘检测算子具有较好的尺度特性,与一阶导数算子相比,搜索极值更加容易,同时能抑制图像的噪声。二维高斯平滑函数G(x,y)由下式给出:
(1)
式中:x,y是图像坐标;σ是高斯分布的标准差。
该函数对原始图像f(x,y)卷积后,采用Laplacian算子获取图像的二阶方向导数图像h(x,y),如下所示:
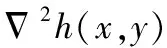
(2)
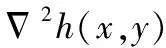
(3)
2.2亚像素边缘定位
2.2.1高斯曲线拟合原理
由于图像边缘灰度梯度近似为高斯曲线分布,用边缘检测算子检测后,可得到灰度变化最大像素的坐标。然而,灰度值变化最大的像素点却不一定是该曲线的极值点,而且往往不是极值点。如图2所示,灰度变化最大像素的坐标是Pmax,很明显该点不是图像的边缘点,实际边缘位置点应该是梯度最大值Fmax对应的点。为了提高芯片测量精度,通过采用亚像素算法精确定位边缘点。对紧挨的3个梯度值F1,F和F2拟合成一条高斯曲线,求出该曲线的均值,就可以精确定位亚像素边缘坐标。

图2 边缘灰度值的变化
2.2.2传统的高斯拟合算法
高斯曲线的表达式如式(1),若直接对其拟合很困难,故作变换,两边取对数得到下式:
(4)
式中:μ为均值;σ为标准差。
上式形如y=ax2+bx+c,是一条典型的x的抛物线,这样求出抛物线顶点坐标即可,使计算大大简化。
设拟合边缘的函数为:
y=ax2+bx+c
(5)
式中:x为像素坐标值;y为像素x处梯度大小的梯度值;a,b,c为曲线参数。
根据最小二乘法原理(误差平方和S最小),有:
(6)
由最小值条件可知S对a,b,c的偏微分都为0,求得:
(7)
式中:
(8)
在上述的求解过程中,应注意到二次曲线是由原高斯曲线取对数得到的,因此式中的y应该用其对数值代替,求的μ和σ:
(9)
式中μ值即为极值点。
利用式(9)的求解结果只能运用于特定的水平、垂直和对角线方向,然而实际检测过程中图像的边缘可能为任意方向,传统算法的定位精度势必受到影响,因此必须对该算法进行优化。
2.2.3算法优化
使用LOG算子进行边缘粗定位后,得到每个边缘像素点的位置。然后使用Hough变换[7]便可以得到边缘切线的斜率,从而得到各个边缘像素点的梯度方向。假设梯度方向与水平轴的夹角是θ,取一定精度像素点的边缘位置为坐标系中心点,旋转该坐标系,使梯度方向和边缘方向分别为x轴和y轴。沿x轴做高斯曲线拟合,便能够得到更精确的亚像素位置。
理论上而言该算法能达到较高精度,但是数字图像的像素是离散分布的,像素的坐标值经旋转后可能不是整数,而像素本身的灰度值又必须明确。为了解决该问题,引入一种灰度值插值[8]的方法。
假设已有像素的灰度值为f(m1,n1),f(m2,n2),…,f(mn,nn),则新坐标系下新的像素灰度值可以表示为:
(10)
式中:h(mi-m0,ni-n0)为插值函数;f(mi,ni)为权重系数,i=1,2,…,n.
插值函数的选择直接决定算法的精度和计算量。考虑到待检测图片所需达到的精度,决定选用拉格朗日插值算法。根据高等数学理论,如果函数f(x)在点x0的某个领域内有从1到(n+1)阶导数,那么该函数在该点附近可以展开为泰勒级数:
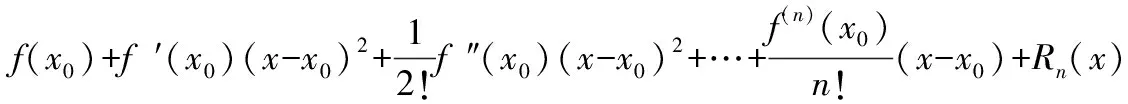
(11)
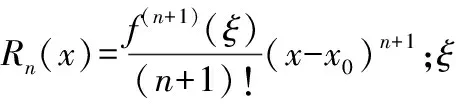
一般情况下,二阶泰勒级数就能满足检测要求。如图2所示,单个像素被一周的4个像素包围,任选其中的3个做拉格朗日插值,求所得数据的平均值,作为像素的新灰度值。

图3 单像素附近点示意图
假设图中点(1,0),(1,1),(0,0),(0,1)的灰度值分别为y1,y2,y3和y4,现以前三项为插值点,对f1(x,y)做二阶泰勒级数展开:

(12)
同理可求f2(x,y),f3(x,y)和f4(x,y),四者的平均值即为插值后的亚像素边缘点f(x,y)。
(13)
3 试验结果及分析
试验中,以实验室标准PCR芯片为检测对象,在Visual Studio 2008平台上,采用ImageSource面阵CCD,12 mm的Computar工业镜头和环形贴片LED前景照明光源,利用该文方法进行定位检测。
3.1旋转不变性试验
为了验证从不同角度检测的亚像素值情况,利用文中系统通过试验验证该算法。首先在芯片图像某一边缘点,求120°处像素值,结果为139.37。然后以该点的亚像素坐标值为中心点,依次旋转直线如表1所示角度,分别求出梯度值和亚像素值。表1中各角度亚像素值不变,证明该算法具有旋转不变性,不影响芯片通道宽度的测量结果。

表1 不同角度直线得到的亚像素值
3.2标准芯片测量试验
PCR芯片通道宽度的理论值为0.450 mm,利用文中系统进行实际测量,处理前后图像和测量软件界面如图4所示。



图4 处理前后图像和测量软件界面
首先利用棋盘标准件对文中系统进行标定,计算出每个像素的实际尺寸为0.013 657 82 mm.使用该系统对芯片通道宽度进行测量,得到八组数据,如表2所示,取该组数据的平均值可得到精确的芯片通道尺寸为0.449 5 mm.与理论值相比,测量偏差极小,精度达到了0.05个像素。
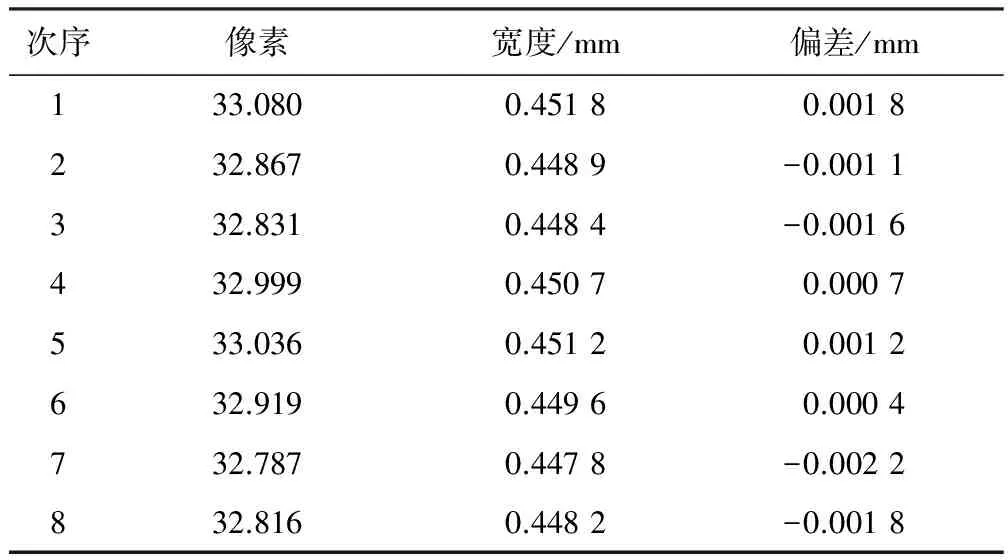
表2 对宽度为0.450 mm的PCR芯片通道测量值
4 结论
面向PCR芯片几何关键参数精密测量的实际需求,在LOG算子粗定位的基础上,在一定窗口内对梯度幅值进行高斯曲线拟合,提出利用Hough变换和灰度插值的方法来解决高斯拟合只能在特殊方向上运用的局限性。试验结果表明:该算法具有旋转不变性,待测芯片放置角度对测量结果没有影响;达到了较高的测量精度,能精确到0.05个像素。
参考文献:
[1]谢定裕.流体力学.天津:南开大学出版社,1987:122-187.
[2]GHOSAL S,MEHROTRA R.A moment-based unified approach to image feature detect.IEEE Transactions on Image Processing,1997,6(6):781-793.
[3]马艳,张治辉.几种边缘检测算子的比较.工矿自动化,2004,1 (2):54-56.
[4]赵芳,栾晓明,孙越.数字图像几种边缘检测算子检测比较分析.自动化技术与应用,2009,28(3):68-72.
[5]杨滨峰,李亚文,赵杰.物体形状检测的亚像素细分算法综述.计算机与数字工程,2011(11):17-20.
[6]屈玉福,浦昭邦,王亚爱.视觉测量系统中亚像素边缘检测技术的对比研究.仪器仪表学报,2003,24(4):460-462.
[7]陈洪波,王强,徐晓蓉,等.基于改进Hough变换的符号线段特征提取.光学精密工程,2003(06):632-636.
[8]胡卫军,万琳,陆永亮.基于灰度插值的MNAM图像表示方法.小型微型计算机系统,2010(8):1558-1561.

