基于稀疏表示的B 型超声图像超分辨重建算法

李斌 李德来 张琼

1 汕头市超声仪器研究所有限公司 （汕头 515041）

2 广东省汕头大学工学院 （汕头 515063）

0.引言

超声由于其实时、安全、廉价等特点，已经成为目前三大主流医学影像设备之一[1]。超声仪器受系统成本和超声本身特点的限制，成像区域相对较小，在检查过程中或者后期的查看中常常需要对图像进行放大处理，更清晰地显示图像中的边缘和细节。为此，如何超分辨率重建放大后的图像成为一个热门的研究课题。

超分辨率技术始于20 世纪60 年代Harris 和Goodman 的研究工作[3～4]，他们将带限信号外推的方法运用于光学图像超分辨重建。由于其应用前景十分广阔，这种技术马上引起了学术界的重视。传统超分辨率重建的是利用低分辨率图像恢复高分辨率图像的逆问题。很多信息在高分辨率图像到低分辨率图像变化的过程中丢失，使得重建问题变成一个严重欠定问题。针对传统超分辨率算法的不足，人们提出了不同的改进算法[5～11].文献[4]提出基于Markov 随机场的学习策略，虽然取得了良好的结果，但是为了获得有足够表达力的数据库，需要大量的图像。在[6]中，作者运用文献[7]中的思想，把低分辨率块空间的局部几何影射到高分辨率块空间，以获得高分辨率块的邻域线性组合。不过，用固定K 值邻域重建会因为过拟合或欠拟合而产生模糊效应。文献[8]提出了一种基于超完备字典求解的图像超分辨率算法，得到较好的实验结果，但是实验参数需要凭经验取得，对噪声比较敏感。

本文为得到更好的重建效果，提出基于稀疏表示的B 型超声图像超分辨率重建算法。对于存在稀疏性的信号，稀疏表示可以得到信号的最优重建效果。为了确保稀疏性，在对B 型超声图像进行深入分析的基础上引入了一种可以快速地构造超完备字典的稀疏编码算法，实现B 型超声图像快速有效的超分辨率重建。

1.稀疏表示理论

近几年基于超完备稀疏分解的信号表示理论得到广泛关注。基本思想是用超完备字典中的冗余基取代传统方法中的正交基。信号的稀疏分解即从超完备字典中选择具有最佳线性组合的若干原子来表示信号，实际上是一种逼近过程[10]：

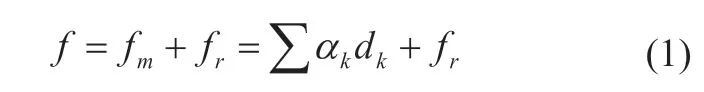
式中：fm为f 的逼近，fr为残差，dk为给定超完备字典D 中的一个原子，αk为稀疏矩阵α 的原子。我们希望在fr方差有限的情况下得到α 最稀疏的解。即：

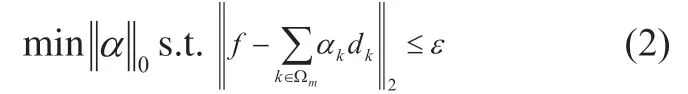
式中：||.||0是零范数，ε 为方差上限。如何求取上式的惟一解是一个典型的NP(Nondeterministic Polynomial)问题。为此，众多学者提出了多种有效的稀疏求解算法，主要有MP（Matching Pursuit）、OMP(Orthogonal Matching Pursuit)及BP(Back Propagation)等。

2.B 型超声图像超分辨率重建算法

通过上面的介绍可知稀疏表示的重建算法包括超分辨率重建和超完备字典的建立两个关键问题，为此，下面分两部分来分别论述。

2.1 基于稀疏表示的超分辨率重建过程

假设低分辨率图像Y 中的每一小块y，在低分辨率字典Dl中存在稀疏表示：

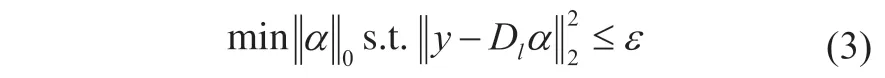
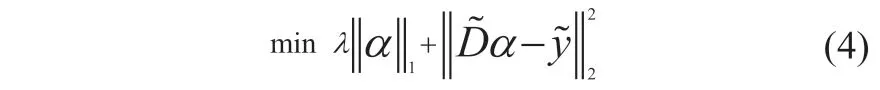
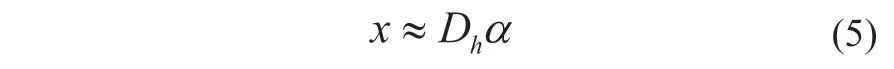
至此，超分辨率重构问题的关键转化为如何构造超完备字典Dh，Dl以及在已知超完备字典的情况下如何快速求解系数α。

2.2 字典的构造

超完备表示中字典D 由一组函数构成，并且至少能张成整个空间。如果要想得到图像最稀疏的表示，则要求所用字典具有有限冗余性[11]。

对任意给定信号 ，可以表示成：

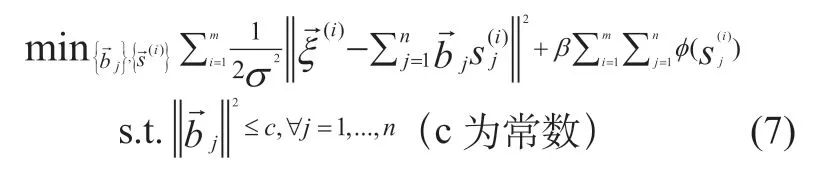
式(7)也可以写成矩阵形式，假定 为输入矩阵， 为基矩阵， 为系数矩阵，那么上述的最优化问题就可以写成：

对于系数矩阵S 的学习，最优化问题等价于正则化最小二乘问题，从而可用最小二乘法求解S。在已知S 后，上式的最优化问题转化为：

从(9)式中求解字典是个具有二次约束的最小二乘问题，本文采用拉格朗日对偶求解。

3.实验结果分析与应用

为验证算法的有效性，我们使用不同检查类型的B 型超声图像进行了测试，结果表明本文算法能更好地重建超分辨超声图像。下面的例子选择一副低分辨率的肝脏图像（133×133 像素）作为输入（图1（a）），使用不同算法对其进行三倍放大，也就是放大后的图像为399×399 像素；然后对比不同算法得到图像在边缘和细节上的保留程度；最后，给出了该算法在“宏云”彩超上的应用效果。

图1. 不同算法超分辨率插值重建结果对比

图1（b）为经典的双三次样条插值算法得到放大后的肝脏图像，图1（c）为本文算法提出的稀疏表示高分辨率重建算法得到的放大后的肝脏图像。通过直观上的对比可以发现本文算法得到的结果在边缘、细节和对比度上都优于双三次样条插值算法。

为了定量分析不同算法得到的结果，本文选择原始图像中包含边缘和细节的某一列（如图2(a)中白色竖线所示）来分析不同算法的差异。图2(b)为双三次样条插值得到结果的对应列上的灰度变化曲线，图2(c)为本文算法得到结果的对应列上的灰度变化曲线。在100 至150 深度方向像素点处本文算法的峰值更大，同时底部更宽，表明本文算法有更好的边缘保护和更高的对比度。同时，从两个灰度变化曲线的对比可以得出：对于弱小的细节，本文算法也能更好地呈现。

上述实验例子很好地证明了本文算法在B 型超声超分辨重建上的优势，图3 给出了本文算法在“宏云”彩超中的实际应用效果。图3 中左下方的小图为原始的凸阵腹部模式下得到的B 型超声试块图像；图中的小框表示需要放大后精细显示的区域；“×3.0”表示对小框区域进行3 倍的放大；大图为超分辨率重建算法得到的放大3 倍后结果。从图中可以看到，重建后的图像边缘清晰、细节丰富、对比度高。

图2. 图像中相同位置的灰度变化曲线对比

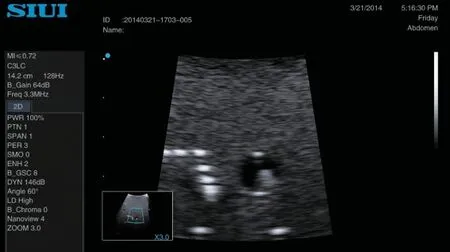
图3. 本文算法在“宏云”彩超上的应用效果

4.结论

在“宏云彩超”的开发中为攻克B 型图像超分辨率重建这一难点问题，结合稀疏表示的最优表示特性，提出一种基于稀疏表示的B 型图像超分辨率重建算法。实验结果证实了本方法的有效性。相比于其他方法，本算法可以得到更突出的边缘、更多的细节和更好的图像对比度。

[1] A. Webb, Introduction to Biomedical Imaging. John Wiley & Sons, Hoboken, 2003 .

[2] 新华网. http://news.xinhuanet.com/tech/2013-11/11/c_125682592.htm.

[3] J L Harris. Diffraction and Resolving Power [J]. Journal of the Optical Society of America, 1964 ,54 (7) : 931-936。

[4] J W Goodman .Introduction to Fourier Optics [M]. McGraw-Hill, New York, 1968.

[5] H. Chang, D.-Y. Yeung, Y. Xiong. Super-resolution through neighbor embedding [C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004, 1: 275–282.

[6] W. T. Freeman, E. C. Pasztor, O. T. Carmichael. Learning low-level vision [J]. International Journal of Computer Vision, 2000, 40(1):25-47.

[7] S. T. Roweis, L. K. Saul. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000.290(5500): 2323-2326.

[8] J. Yang, J. Wright, T. Huang, Y. Ma, Image super-resolution as sparse representation of raw image patches [C]. In Intl. Conf. on Comp. Vis. and Patt. Recog. 2008:1-8.

[9] 张丹莹,李翠华,李雄宗等. 一种基于去冗余字典的图像去噪算法[J].厦门大学学报(自然科学版),2012,51(4):691-695.

[10] J. A. Tropp. Topics in sparse approximation [M]. PhD Dissertation, Stanford University, Stanford, CA, 1995.

[11] H. Lee, A. Battle, R. Raina, A. Ng. Efficient sparse coding algorithms [C]. In NIPS, 2007: 801-806.