基于频率分布函数的异类数据关联∗

孙贵东,关 欣,常 进,张 婕

(1.海军航空工程学院电子信息工程系,山东烟台264001;2.海军航空工程学院通信站,山东烟台264001)

0 引言

传感器类型不同会产生异类量测数据[1-9],增加了信息融合的不确定性,序列数据和区间数[10-13]作为不确定性数据的重要表现形式在数据关联领域值得研究。由于序列数据和区间数据在数据类型上的限制,使得传感器探测到的序列类型数据无法直接和区间数据进行关联,所以关于序列、区间异类数据类型的关联研究是必要的,能够有效地解决异类数据导致的数据关联的不确定性,提高关联率。序列、区间异类数据的关联在传感器数据关联领域研究的相对较少,现有的方法大多是同型数据的关联方法,所以本文从两种类型数据之间的不确定性度量入手,首先对序列数据进行区间转化,使得异类数据同型化,再从区间多属性关联理论[14-30]的角度出发,采用区间关联度作为关联指标进行数据关联。其中,基于序列数据的频率分布函数进行序列、区间异类数据同型转化,用转化后的区间数据组来表示序列数据。最后通过仿真实例,验证了该方法在序列、区间异类数据关联上的合理性和优越性,得到了合理的关联结果。

1 序列、区间同型转化

1.1 序列、区间的描述

定义序列为

式中,Si表示序列的第i个分量,n为序列的长度。

记区间数为

也可以记为

式中,a-=a-Δ,a+=a+Δ,a-≤a+,特别地当a-=a+时,区间数A退化为实数。

1.2 频率分布函数

对于长度为n的序列S,利用统计规则统计其中的可能元素S i(i=1,2,…,m,m≤n)出现的个数记为y,则称y=f(S i)为序列S的频率分布函数,则有

1.3 序列的区间表示

根据频率分布函数的定义对序列数据S进行频数统计,形成频率分布函数,为了提高计算精度和效率,采用检测门限σ进行检测,即满足下式的元素保留,舍去频数过低的数据点的影响,取其中高频数作为主要部分。

假设经过检测后剩下的频率分布函数包含l个可能元素,记为S i(i=1,2,…,l,l≤m≤n)则有

式中,l为满足检测后剩下的序列可能值的个数,也就是序列转化的区间个数。对于可能值S i及其对应的频率分布函数f(S i),假设转化后的区间中点即为S i,区间端点到中点的距离为S i对应原数据的方差记为var(S i),则序列的区间转化可以表示为

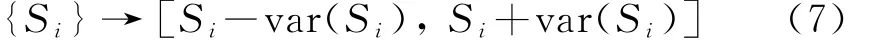
则每一个可能值对应的序列数据可以转化为一个区间组：

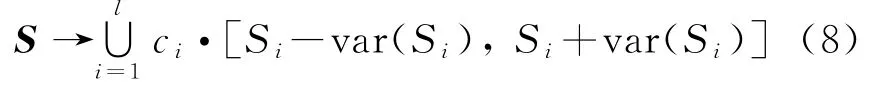
式中,c i为序列经频率分布函数区间转化后得到的区间权重,且

c i可以保证序列变换为区间的保真性,还原了变换后区间在原序列中所占的重要性。

定义序列经区间转换的区间数据利用率定义为

1.4 模式唯一性判断

频率分布函数是通过统计规律得出序列可能值,并形成区间,此过程是一个统计过程需要的序列数据量较大,是传感器量测累积一段时间后上报的数据,而在累积过程中被测目标的模式可能不唯一,所以需要对转化后的区间所描述的模式进行唯一性判断。可以通过频率分布函数转化后的可能值S i的离散程度来判断区间所描述的模式,记离散程度为

式中,¯S i为可能值S i的均值,且

即对于给定的门限η,如果

则判定经频率分布函数转化后的区间描述的目标模式唯一。

2 序列、区间异类数据关联算法

2.1 算法描述

假设目标关联序列数据集集合为T={T1,T2,…,T i,…,T m},其中m为序列序号,表示关联类,T i为序列数据集,由多属性序列组成。关联区间数据集集合为I={I1,I2,…,I i,…,I n},其中I i为区间数据集,与序列数据集类似,由物理关系对应的属性区间组成。属性参数集为P={P1,P2,…,P num},其中num为属性参数种类序号,表示每一类目标都具有num类属性参数。则关联的问题变成在多属性集P下,序列关联集T i(i=1,2,…,m)和区间关联集I j(j=1,2,…,n)的配对问题。

2.2 算法步骤

假设关联数据已经经过标准化处理,考虑单属性P k作用下序列关联集T i(i=1,2,…,m)和区间关联集I j(j=1,2,…,n)的关联。首先对属性P k对应的序列关联序列T ik=(t ik1,t ik2,…,t ikd)进行区间化表示,根据1.3节所述的基于频率分布函数的区间化表示方法可得

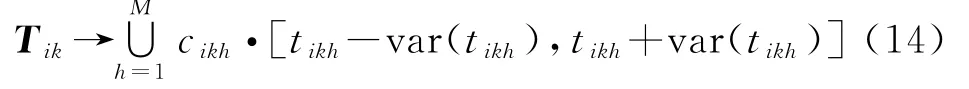
式中,M为序列区间化转化后的区间个数,则序列、区间异类数据问题就变成区间关联问题。

计算转化后的区间与属性P k对应的序列区间之间的区间距离为

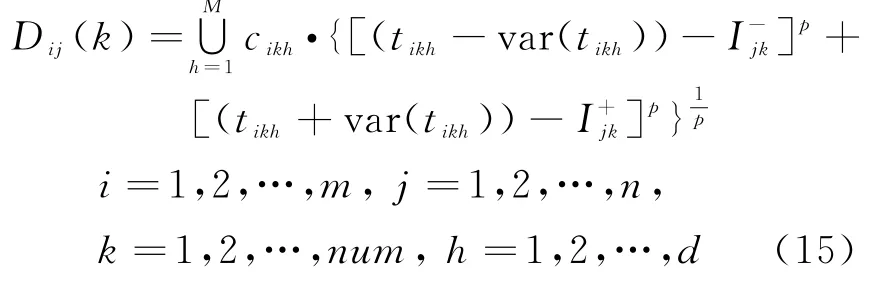
在实际计算过程中一般选取p=2,即加权Euclidean距离计算。

则区间关联系数可以表示为

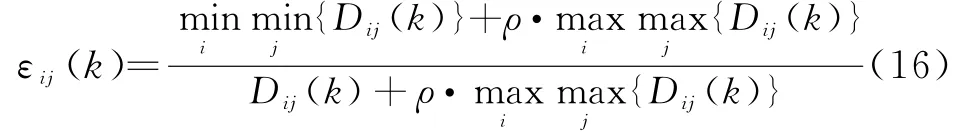
式中,ρ为分辨系数,ρ∈[0,1]。则多属性条件P下的序列关联集T i(i=1,2,…,m)和区间关联集I j(j=1,2,…,n)的关联度为

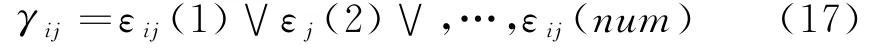
在实际计算中,对于多属性组合运算∨常采用加权融合的方法进行计算,权重的确定可以根据属性参数在关联过程中的重要程度,利用Delphi调查法、AHP法、熵权法等来确定,这里不再讨论。

设权重向量为

则多属性条件下的区间关联度加权组合为

通过上述处理可以得到多属性条件下的序列关联集T i(i=1,2,…,m)和区间关联集I j(j=1,2,…,n)的关联度集为

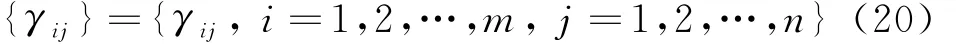
根据γij的大小按照最大关联度关联准则可以得到序列关联集T i(i=1,2,…,m)与区间关联集I j(j=1,2,…,n)之间的关联对。

3 仿真分析

3.1 仿真环境

假设存在关联序列T1和T2,64类关联区间集I1,I2,…,I i,…,I64,关联数据均具有3类属性特征参数,分别记为P1,P2和P3。现要判定两类关联序列T1和T2在多属性条件下分别与64类关联区间I1,I2,…,I i,…,I64中的哪类数据相互关联。实验仿真数据序列按下式产生。

式中,α为服从均匀分布的离散序列值,β为服从高斯分布的离散序列值,c为高斯分布的标准差。

3.2 仿真实验

实验中每条关联序列的关联方法是一样的,所以以序列T1为例研究,根据2.2节给出的序列、区间异类数据关联算法,首先形成3类属性参数的频率分布函数如图1所示。

对频率分布函数区间化生成得到3类属性参数对应的序列、区间异类数据转化区间为

3类属性参数对应的序列、区间异类数据组合权重向量分别为

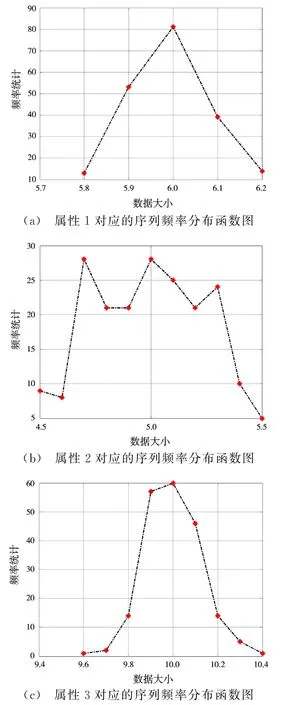
图1 序列T1的频率分布函数图

则利用数据利用率的定义式(10)计算三类属性特征的数据利用率分别为100%,84%,95.5%。数据利用率较高,均达到了80%以上,说明经过频率分布函数变换后的区间表示能够充分反映序列数据所描述的原有属性信息。

3类属性参数对应的序列、区间异类数据区间加权组合为

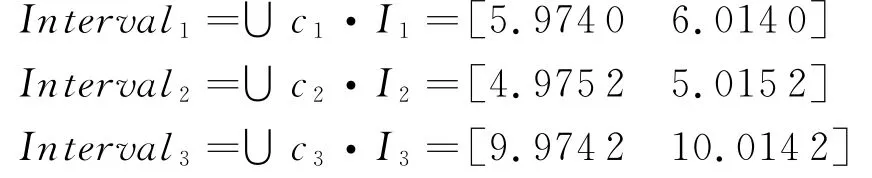
按照多属性区间关联方法计算转化后的区间值,其与64类区间集关联度变化如图2所示。

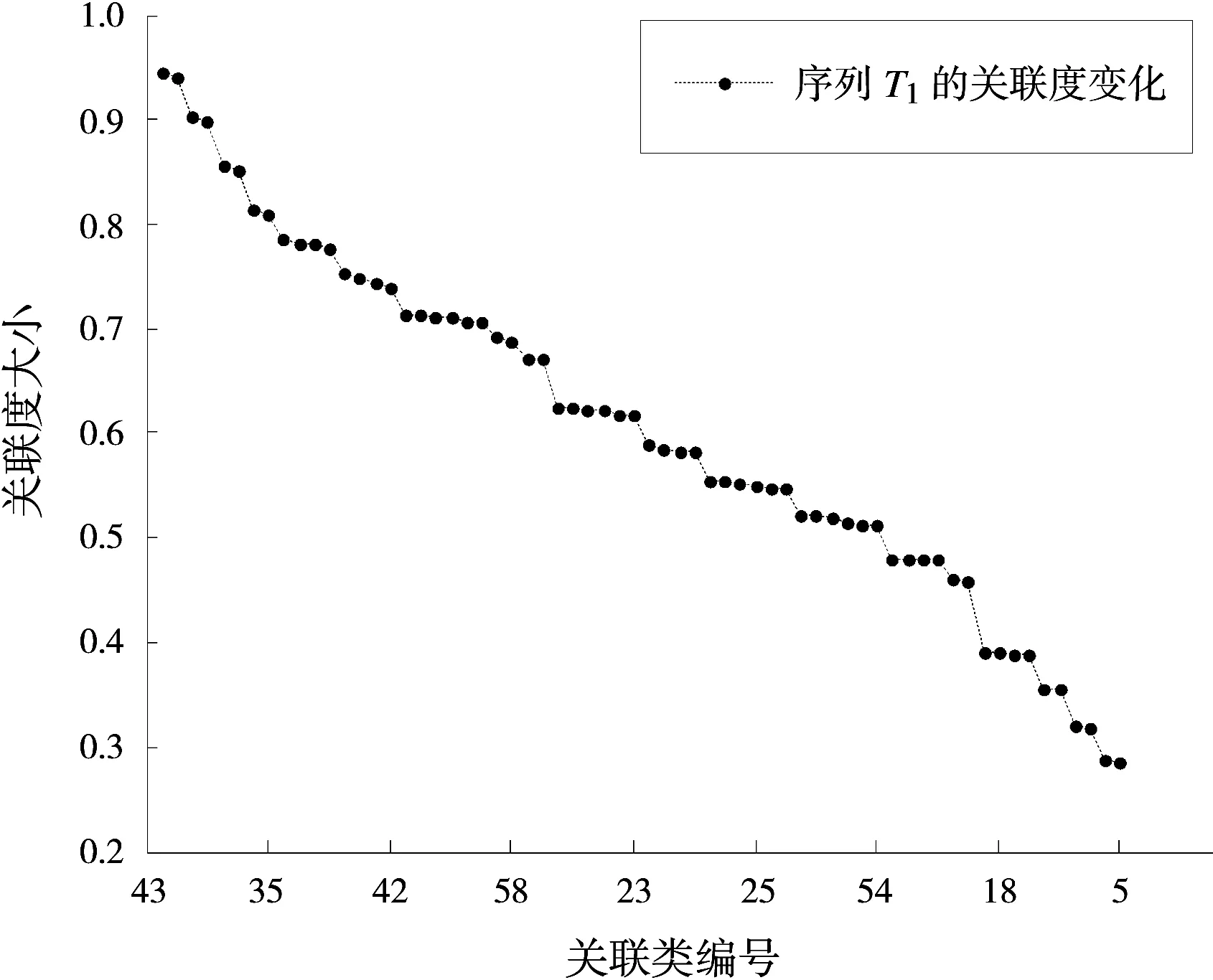
图2 序列T1与64类区间数据的关联度变化图

图2中纵坐标为关联度大小,横坐标为序列T1与64类区间集关联度大小排序编号,具体编号排序为

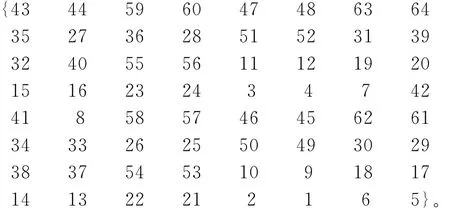
根据关联度大小和编号排序得知,序列T l与第43类区间数据的关联度最大,关联度达到94.5%,所以最大相似度关联准则可以判定序列数据T1与区间数据I43为关联对。

同理可以按照上述步骤,计算得到关联序列T2的关联度排序编号为

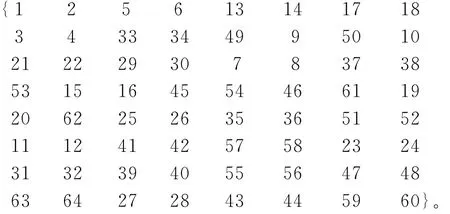
得知序列T2与区间数据I1为关联对,关联度达到93.6%。

3.3 算法性能对比

本对比实验将本文算法与一种序列最值区间形成关联法进行对比。所谓最值区间形成关联法即对于序列的区间转化采用的是一种直接将序列数据中的最小值和最大值分别作为转化后的区间上下限的方法,即对于序列S=(S1,S2,…,S i,…,S n),按最值区间法转化为

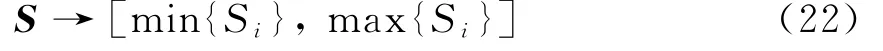
则按照本文算法和序列最值区间形成关联法对文中T1序列的关联计算结果如图3所示。

图3 序列T1与四类区间数据的关联度变化图

图3中纵坐标为关联度大小,横坐标为关联类数目编号,在经过100次仿真处理后,本文所述的频率统计区间法的关联结果始终为T1与区间数据I43为关联对,而最值区间法最大关联度对应的编号在{43 44 59 60}之间变化,得到的关联结果不稳定。

根据上述实验可以得知,利用本文所述的频率统计区间法计算的关联度区分度较高,而且正确关联度也较高,达到90%以上。而最值区间法尽管关联度也接近90%,但是计算的关联度分布集中,这就造成对关联类的区分模糊,在模糊度较大的情况下不能很好地进行关联判断。主要原因是因为最值区间法是利用序列的最值形成区间进行关联的,这样在序列不稳定时,最值范围不能有效地反应整条序列内部具体的数据分布,造成转化后的区间误差较大,而频率统计区间法是对序列内部具体细微的分析,能够反应序列内数据的分布情况,因而转化后的区间更能反映序列的变化,所以计算的关联度较高,区分度较好。

4 结束语

针对传感器探测的目标多属性序列类数据不能直接与区间类型数据进行关联的问题,本文从两种类型数据之间的不确定性度量入手,提出了基于频率分布函数的序列、区间异类数据关联算法,利用频率分布函数实现了序列、区间的同型转化,在此基础上利用多属性区间关联理论进行关联判定,成功地解决了序列-区间异类数据的关联问题,得到满意的关联结果。为描述目标多属性的序列、区间异类数据的关联问题提供了一种可行的解决方法,在异类传感器数据融合领域具有现实意义。

[1]黄友澎,曹万华,张志云,等.基于灰色关联分析的异类传感器航迹相关算法[J].华中科技大学学报(自然科学版),2011,39(10)：83-86.

[2]崔博鑫,许蕴山,向建军,等.一种基于异类传感器信息融合的目标识别方法[J].计算机工程与应用,2012,48(24)：113-116.CUI Boxin,XU Yunshan,XIANG Jianjun,et al.Target Recognition Method Based on Heterogeneous Sensors Information Fusion[J].Computer Engineering and Applications,2012,48(24)：113-116.(in Chinese)

[3]DAI Yaping,WANG Junzheng.Asynchronous Data Fusion of Two Different Sensors[J].Journal of Beijing Institute of Technology,2001,10(4)：402-405.

[4]刘德浩,王国宏,陈中华.基于EM-EKF的异类传感器系统误差配准算法[J].雷达科学与技术,2011,9(5)：453-456.LIU De-hao,WANG Guo-hong,CHEN Zhong-hua.A Registration Algorithm of Different Sensors Based on EM-EKF[J].Radar Science and Technology,2011,9(5)：453-456.(in Chinese)

[5]龙海鹰,任清安.空管异类传感器数据融合算法研究[J].雷达科学与技术,2010,8(6)：526-531.LONG Hai-ying,REN Qing-an.Research on Data Fusion Algorithm of ATC Heterogeneous Sensors[J].Radar Science and Technology,2010,8(6)：526-531.(in Chinese)

[6]曹晓军,彭会萍.基于相似性测度的异类传感器的数据融合算法[J].计算机应用与软件,2012,29(5)：130-131.CAO Xiaojun,PENG Huiping.A Data Fusion Algorithm for Heterogeneous Sensor Based on Similarity Measures[J].Computer Applications and Software,2012,29(5)：130-131.(in Chinese)

[7]韩崇昭,朱洪艳,段战胜,等.多源信息融合(第2版)[M].北京：清华大学出版社,2010：478-495.

[8]何友,王国宏,关欣,等.信息融合理论及应用[M].北京：电子工业出版社,2010：251-260.

[9]杨万海.多传感器数据融合及其应用[M].西安：西安电子科技大学出版社,2004：84-101.

[10]胡启洲,张卫华.区间数理论的研究及其应用[M].北京：科学出版社,2010：15-18.

[11]曾文艺,赵宜宾.基于区间数度量的区间值模糊集合的归一化距离、相似度、模糊度和包含度的关系研究[J].模糊系统与数学,2012,26(2)：82-90.

[12]曾文艺,赵宜宾.基于区间数度量的区间值模糊集合的贴近度和模糊度的关系[J].模糊系统与数学,2012,26(1)：25-31.

[13]赵宜宾,曾文艺.基于区间数度量的区间值模糊集合的相似度、模糊度和包含度的关系研究[J].工程数学学报,2010,27(2)：295-304.

[14]卫贵武.区间数多指标决策问题的新灰色关联分析法[J].系统工程与电子技术,2006,28(9)：1358-1359.WEI Gui-wu.New Method of Grey Relational Analysis to Multiple Attribute Decision Making with Intervals[J].Systems Engineering and Electronics,2006,28(9)：1358-1359.(in Chinese)

[15]胡丽芳,关欣,何友.一种新的灰色多属性决策方法[J].控制与决策,2012,27(6)：896-898.

[16]万树平.不确定多传感器目标识别的区间相离度法[J].控制与决策,2009,27(9)：1306-1309.

[17]罗党.基于正负靶心的多目标灰靶决策模型[J].控制与决策,2013,28(2)：241-246.

[18]丁传明,黎放,齐欢.一种基于相似度的混合型多属性决策方法[J].系统工程与电子技术,2007,29(5)：737-740.

[19]王正新,党耀国,宋传平.基于区间数的多目标灰色局势决策模型[J].控制与决策,2009,24(3)：388-392.

[20]WU Sheng,ZHANG Zhi-yong.A New Incidence Degree Model of Interval Grey Number Based on Space Mapping[C]∥2011 IEEE 18th International Conference on Industrial Engineering and Engineering Management,Changchun：IEEE,2011：8-10.

[21]YAN Shuli,LIU Sifeng.Grey Incidence Method of Decision-Making with Three-Parameter Interval Numbers and Unknown Weights[C]∥2011 IEEE International Conference on Grey Systems and Intelligent Services,[S.l.]：[s.n.],2011：582-585.

[22]ZHENG Qing-li,GUAN Ye-qing.A New Grey Incidence Model of Interval Numbers and Its Application[C]∥2011 IEEE International Conference on Systems,Man,and Cybernetics,Anchorage,AK：IEEE,2011：1881-1885.

[23]XU Zeshui.On Similarity Measures of Interval-Valued Intuitionistic Fuzzy Sets and Their Application to Pattern Recognitions[J].Journal of Southeast University(English Edition),2007,31(11)：139-143.

[24]ZHANG Yingjun,MA Peijun,SU Xiaohong.Pattern Recognition Using Interval-Valued Intuitionistic Fuzzy Set and Its Similarity Degree[C]∥2011 IEEE International Conference on Intelligent Computing and Intelligent Systems,[S.l.]：[s.n.],2009：361-364.

[25]XU Z,LIU M,YANG G,et al.Application of Interval Analysis and Evidence Theory to Fault Location[J].IET Electric Power Applications,2009,3(1)：77-84.

[26]SHI Hongxing,LIU Sifeng,DU Hongyun,et al.Study on the Absolute Grey Incidence Model of an Interval Grey Number Sequence[C]∥2008 IEEE International Conference on Systems,Man and Cybernetics,[S.l.]：[s.n.],2008：1664-1667.

[27]DENG J L.Introduction to Grey System Theory[J].Journal of Grey System,1989,1(1)：1-24.

[28]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社,2002：135-162.

[29]刘思峰,党耀国.灰色系统理论及其应用[M].北京：科学出版社,2010：62-92.

[30]党耀国,刘思峰.灰色预测与决策模型研究[M].北京：科学出版社,2009：114-119.