两端对称缺陷对对称结构光子晶体透射谱的影响

苏 安，蒙成举，高英俊，潘继环

(1．河池学院物理与机电工程学院，广西宜州546300;2．广西大学物理科学与工程技术学院，广西南宁530004)

1 引言

光子晶体［1－2］概念提出近30年来，其潜在的应用价值已经引起世人的广泛关注并取得了一系列的研究成果。作为一种人工薄膜光学材料，其最奇异的光学特性是存在光子带隙，这使光子替代电子传输信息成为可能，并具有巨大的应用前景［3－12］。

缺陷［7－11］是破坏光子晶体周期性排列结构，即在光子晶体组成介质间插入的不同介质。准周期性排列的光子晶体透射谱一般由禁带和通带交替排列形成，当光子晶体中插入缺陷后，可使禁带中出现缺陷模——透射峰，调整缺陷的位置或参数即可改变缺陷模的频率位置或性能［7－11］。在已有的文献报道中，往往都是在光子晶体组成介质的某个部位插入缺陷，而在两端特别是镜像对称结构的光子晶体两侧插入对称缺陷的研究还很少见。当在镜像对称结构的两侧加入缺陷时，缺陷就象光量子阱两侧的垒层一样，可增强光子晶体对入射到其中光场的局域限制作用，从而改变光子晶体透射谱的特性［3－6，9－10］。基于这种思路，本文在构造镜像对称结构光子晶体(AB)n(BA)n的基础上，在其两侧加入缺陷层形成ACmB(AB)n(BA)nBCmA光子晶体结构，并绘制出缺陷层取不同参数时光子晶体的透射谱，找出两端对称缺陷对镜像对称结构光子晶体透射谱的影响规律，为光子晶体的理论研究和实际设计提供参考。

2 研究模型和方法

研究模型为一维光子晶体结构ACmB(AB)n(BA)nBCmA，其中C是插入到镜像对称结构光子晶体(AB)n(BA)n两端的缺陷。各层介质的参数分别为:折射率 nA=4．1，nB=2．35，nC=1．35，介质层厚度dA=763 nm，dB=1329 nm，dC=nAdA/nC，即缺陷层的的光学厚度DC等于A介质层的光学厚度DA。

鉴于研究的主要对象是光子晶体的透射谱，所以研究、计算方法采用比较直观且成熟的传输矩阵法［3－12］。传输矩阵法最突出的优势就是可以用一个传输矩阵描述光在每层介质中的行为，光在光子晶体中的行为则可用一个总传输矩阵表示，总传输矩阵为各分层矩阵之积，由该总传输矩阵即可计算出光通过光子晶体后光的各种传输指标，如光场在光子晶体内部的局域强度，光被光子晶体表面反射的反射系数和反射率，光透过光子晶体的透射系数和透射率等。传输矩阵法理论的详细介绍可见文献［12］，在此不再详述。

3 计算结果与分析

3．1 无缺陷时光子晶体的透射谱

在两侧插入缺陷之前，光子晶体(AB)n(BA)n是普通的镜像对称结构模型，分别取周期数n=2、3、4、5、6，考虑光正入射到光子晶体表面，通过计算机数值计算模拟，得出光子晶体的透射谱，如图1所示，图中横坐标用归一化频率ω/ω0表示单位。图1透射谱的特征符合镜像对称结构光子晶体透射谱的特征，即在宽大的禁带中心出现一条透射带(或透射峰)，其形成原因是镜像对称结构光子晶体的周期性排列中心总存在一个空位缺陷，(AB)n(BA)n可排列成ABAB…AB A BA…BABA，其中A就是对称中心缺失A介质而形成的空位缺陷，所以在禁带中心形成缺陷模。从图1还看到，随着对称周期数n的增大，光子晶体禁带中的透射带会越来越窄最终趋向于窄透射峰，但透射带(或透射峰)所处的频率位置、透射峰数目及透射率等均不变。可见，此镜像对称结构光子晶体的透射谱也具有镜像对称结构的特征，而且透射谱的对称性不随光子晶体的周期数变化而改变［9－11］。透射谱的这种特性可为设计固定通道的光学滤波器件提供理论依据。

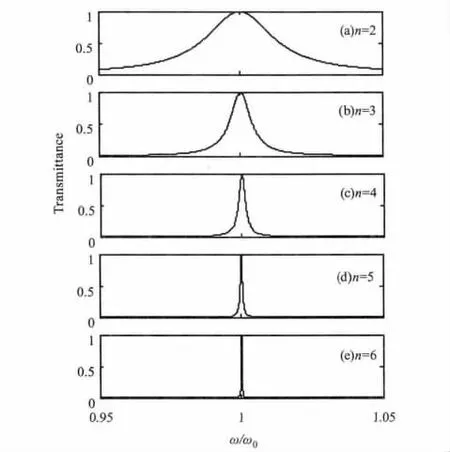
图1 光子晶体(AB)n(BA)n的透射谱Fig．1 Transmission spectrum of Photonic Crystal(AB)n(BA)n

3．2 缺陷折射率n C对透射谱的影响

为研究两端对称缺陷对镜像对称结构光子晶体透射谱的影响，我们固定镜像对称结构光子晶体的排列周期数n=5，即(AB)5(BA)5，然后在光子晶体两端的AB介质中插入缺陷C，形成两端对称缺陷光子晶体结构ACmB(AB)5(BA)5BCmA，模型中m是缺陷层C的排列周期数。显然，两端插入缺陷C后光子晶体仍然满足镜像对称结构，而其透射谱对缺陷的响应如何，我们可作如下研究。

首先，保持光子晶体其他参数不变，取缺陷层C的介质折射率 nC=1．15、1．25、1．35、1．45、1．55，则两端对称缺陷对称光子晶体AC5B(AB)5(BA)5BC5A的透射谱如图2所示。从图2可见，随着两端对称缺陷折射率nC增大，禁带中透射峰的带宽也随之变宽，如以半高全宽描述透射峰或透射带的带宽(下同)，则当 nC=1．15时，透射峰带宽为 Δω =3．8 ×10－4ω/ω0，nC=1．55时，Δω =1．7 ×10－3ω/ω0;而且随着nC增大禁带中心的透射峰会逐渐向高频方向移动，nC=1．15 时，透射峰中心处于 0．999ω/ω0频率处，nC=1．55 时，透射峰中心则处于 1．004ω/ω0频率处。对比(AB)n(BA)n的透射谱特性可知，两端插入对称缺陷后，随着缺陷折射率的变化，光子晶体的透射谱不再具备镜像对称结构的特性。但利用两端对称缺陷折射率对镜像对称结构光子晶体透射谱的调制规律，可指导宽带滤波器和光学开关的设备。

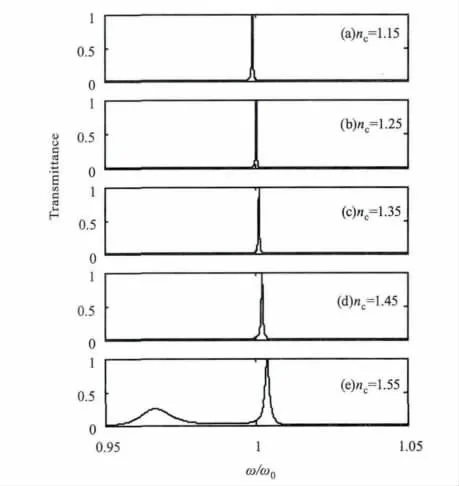
图2 nC对AC5 B(AB)5(BA)5 BC5 A透射谱的影响Fig．2 Transmission spectrum of AC5 B(AB)5(BA)5 BC5 A versus nC

3．3 缺陷光学厚度D C对透射谱的影响

由光子晶体的模型参数可知，缺陷层的厚度DC是以A介质层的光学厚度DA来度量的，因此，保持光子晶体ACmB(AB)5(BA)5BCmA的其他参数不变，分别取两端缺陷层的光学厚度DC=1DA、2DA、3DA、4DA、5DA、6DA、7DA、8DA变化，计算绘制出光子晶体的透射谱如图3所示。

从图3可见，两端对称缺陷光子晶体透射谱对缺陷光学厚度奇偶倍数的响应不同，当DC为DA的奇数倍时，禁带中心出现一条带宽比较宽的通带，而且当DC奇数倍增大时，通带中心保持在1．0ω/ω0频率位置不变，但通带迅速变窄，当DC=1DA时，Δω =2．46 × 10－2ω/ω0，当DC=7DA时，Δω =1．16× 10－2ω/ω0。同时，通带上方出现振荡，振荡峰的数目等于3条，而且振荡峰随DC按DA奇数倍增大而快速生长，如图3(a)、(b)、(c)、(d)所示。可以预测，当DC随DA奇数倍增大到一定数值时，剧烈的振荡将使通带变成3条透射峰。当DC为DA的偶数倍时，禁带中心则出现一条窄透射峰，而且DC偶数倍增大时，该窄透射峰中心保持在1．0ω/ω0频率位置不变，但窄透射峰的带宽缓慢变窄，利用计算机程序对图3(e)～(h)中的各窄透射峰的半高全宽进行测量得:当 DC=2DA时，Δω =2．83 × 10－4ω/ω0，当DC=8DA时，Δω =2．61 × 10－4ω/ω0。

图3 DC对AC5 B(AB)5(BA)5 BC5 A透射谱的影响Fig．3 Transmission spectrum of AC5 B(AB)5(BA)5 BC5 A versus DC

可见，两端对称缺陷光学厚度对光子晶体透射谱对称性没有影响，但对透射谱的带宽影响明显，而且影响具有奇偶性。如果要设计窄带光学滤波器件时，可考虑以DC随DA偶数倍变化作为调制机制，而如果要设计宽带光学器件时，则可选择DC随DA奇数倍变化作为调制机制。

3．4 缺陷周期数m对透射谱的影响

在其他参数不变的条件下，取缺陷层的周期数m=1，2，3，4，5，6，7，8，通过计算机数值计算模拟，可得光子晶体ACmB(AB)5(BA)5BCmA的透射谱，如图4所示。

从图4可见，对称缺陷层的周期数对光子晶体的透射谱影响同样具有奇偶性:当周期数m为奇数时，光子晶体的禁带中出现一条带宽较宽的透射通带，随着m奇数倍增大，该通带逐渐变窄，当m=1 时，Δω =3．22 × 10－2ω/ω0，当 m=7 时，Δω =2．22 × 10－2ω/ω0。同时，通带上方出现振荡，振荡峰的高度比较低，即振荡不剧烈。另外，随着周期数m为奇数倍增大，禁带中的通带中心保持在1．0ω/ω0频率位置不变，如图4(a)、(b)、(c)、(d)所示。当周期数m为偶数时，光子晶体的禁带中则出现一条窄带透射峰，随着m偶数倍增大，该窄带透射峰的透射率和中心位置保持在1．0ω/ω0频率位置不变，但窄透射峰的带宽非常缓慢的变窄，通过计算机程序对图3(e)～(h)中的各窄透射峰的半高全宽进行测量得:当m=2时，Δω =2．89 ×10－4ω/ω0，当m=8 时，Δω =2．85 × 10－4ω/ω0。由于透射峰带宽随 m偶数倍增大时变化比较慢，所以出现图4(e)～(h)透射谱中的窄透射峰带宽不变的“假象”。

图4 m对AC m B(AB)5(BA)5 BC m A透射谱的影响Fig．4 Transmission spectrum of ACm B(AB)5(BA)5 BC m A versus m

可见，两端对称缺陷排列周期数对光子晶体透射谱对称性也没有影响，但对透射谱的带宽影响明显，而且影响也具有奇偶性。当要设计窄带光学滤波器件时，可考虑周期数m以偶数倍变化作为调制机制，而如果要设计宽带光学器件时，则应选择周期数m以奇数倍变化作为调制机制。

4 结论

利用传输矩阵法理论，通过计算机数值计算模拟的方式，研究两端对称缺陷对对称结构一维光子晶体光子晶体ACmB(AB)n(BA)nBCmA透射谱的影响，得出如下结论:

(1)当两端不存在缺陷时，光子晶体透射谱具有镜像对称性，而且镜像禁带中心的单条透射峰随着光子晶体(AB)n(BA)n周期数n的增大而变得细窄，但周期数n不影响透射谱的对称性结构。

(2)随着两端对称缺陷层折射率nC的增大，光子晶体透射谱不再具有对称性，透射峰向高频方向移动的同时带宽逐渐变宽。

(3)两端对称缺陷的光学厚度和排列周期数对光子晶体透射谱的对称性没有影响，但对带宽产生影响，且影响具有奇偶性。随着缺陷光学厚度和排列周期数奇数倍增大，禁带中心出现较宽的透射带，而且透射带会逐渐变窄，同时透射带上方出现振荡峰;随着缺陷光学厚度和排列周期数偶数倍增大，禁带中心出现单条窄透射峰，而且透射峰带宽也会逐渐变窄。

两端对称缺陷对对称结构一维光子晶体光子晶体透射谱的影响规律，为光子晶体设计宽带、窄带光学滤波器件或光学开关等提供指导。

［1］ Yablonovitch E．Inhibited spontaneous emission in solid －state physics and electronics［J］．Phys．Rev．Lett．，1987，58(20):2059－2061．

［2］ John S．Strong localization of photons in certain disordered dielectric superlattices［J］．Phys．Rev．Lett，1987，58(23):2486－2489．

［3］ SU An，GAO Yingjun．Light propagation characteristics of one－dimensional photonic crystal with double－barrier quantum well［J］．Acta Physica Sinica，2012，61(23):234208．(in Chinese)苏安，高英俊．双重势垒一维光子晶体量子阱的光传输特性研究［J］．物理学报，2012，61(23):234208．

［4］ SU An，MENG Chenju，GAO Yingjun．Modulation of activated impurity on filter property of photonic crystal quantum well［J］．Chinese Journal of Lasers，2014，41(3):0306001．(in Chinese)苏安，蒙成举，高英俊．激活性杂质对光子晶体量子阱滤波 器 特 性 的 调 制［J］．中 国 激 光，2014，41(3):0306001．

［5］ SU An，GAO Yingjun，MENG Chenju．Localized electric field of one－dimensional photonic crystal quantum well of double barrier［J］．Acta Photonica Sinica，2014，43(2):0216002．(in Chinese)苏安，高英俊，蒙成举．双重势垒一维光子晶体量子阱内部 局 域 电 场 分 布［J］．光 子 学 报，2014，43(2):0216002．

［6］ SU An，MENG Chengju，GAO Yingjun．Filter with one －dimensional photonic crystalquantum well possessing high－ quality filtering functions［J］．Chinese Journal of Lasers，2013，40(10):1006001．(in Chinese)苏安，蒙成举，高英俊．实现高品质滤波功能的一维光子晶体量子阱滤波器［J］．中国激光，2013，40(10):1006001．

［7］ SU An，LIXianji．Defectmodes of one － dimensional photonic crystal for realizablemultiple channeled filter［J］．Laser＆ Infrared，2010，40(5):0532 － 0536．(in Chinese)苏安，李现基．实现多种通道滤波功能的一维光子晶体缺陷模［J］．激光与红外，2010，40(5):0532 －0536．

［8］ YANG Fan，TANG Jiyu，YANG Shudong，et al．Doped modes of MgF2/CdSe one－dimensional photonic crystal with Ta2O5in visible region［J］．Laser ＆ Infrared，2011，41(11):1253 －1257．(in Chinese)杨帆，唐吉玉，杨述东，等．一维光子晶体MgF2/CdSe及其缺陷结构的反射性质［J］．激光与红外，2011，41(11):1253－1257．

［9］ PAN Jihuan，SU An，MENG Chengju，et al．Effect of barrier layer periodicity asymmetry on photonic crystal quantum well transmission spectrum［J］．Laser＆ Optoelectronics Progress，2014，51(01):012701．(in Chinese)潘继环，苏安，蒙成举，等．垒层周期不对称度对光量子阱透射谱的影响［J］．激光与光电子学进展，2014，51(01):012701．

［10］ SU An，QIN Zongding，GAO Yingjun．Transmission properties of one－dimension photonic crystal quantum well with mirror symmetry structure［J］．Laser ＆ Infrared，2011，41(8):0889 －0993．(in Chinese)苏安，覃宗定，高英俊．镜像对称结构一维光量子阱的光传输特性［J］．激光与红外，2011，41(8):0889 －0993．

［11］ MENG Chengju，SU An．Absorption's influence on the transmission spectrum ofmirror symmetry one－dimension photonic crystal［J］．Laser ＆ Infrared，2011，41(11):1248 －1252．(in Chinese)蒙成举，苏安．吸收对镜像对称一维光子晶体透射谱的影响［J］．激光与红外，2011，41(11):1248 －1252．

［12］ WANG Hui，LIYongping．An eigenmatrixmethod for obtaining the band structure of photonic crystals［J］．Acta Physica Sinica，2001，50(11):2172 －2178．(in Chinese)王辉，李永平．用特征矩阵法计算光子晶体的带隙结构［J］．物理学报，2001，50(11):2172 －2178．