大气湍流下激光斜程通信误码率分析

吴 郁，周亚民，王忠思，刘 兵

(海军士官学校三系，安徽蚌埠233012)

显然，将式(2)、(3)代入式(4)，就可以得到湍流条件下系统误码率的数学计算模型。

1 引言

在自由空间无线激光通信中，由于大气湍流效应的影响，激光会产生光强闪烁、光束扩展等，这都使得接收光强产生随机变化，进而引起接收信噪比降低，传输误码率增大，甚至会造成通信中断，导致通信系统性能下降，影响通信系统的稳定性和可靠性［1，2］。

针对大气湍流条件下的光波传输问题，国内外许多学者做了大量的研究。20世纪60年代开始，Tatarskii和 Chernov［3－4］基于 Rytov 近似，得出了研究水平空间传播的Rytov方法。然而大量的实验数据表明，Rytov方法仅适用于弱起伏区，对于中等强度以上的大气湍流，Rytov方法不再适用。修正Rytov方法［5－6］将经典 Rytov方法扩展到中等湍流和强湍流区的闪烁研究，但依然只能解决大气结构常数不变的水平空间传输问题。而对于光波斜程传输，Andrews［7］等研究了零内尺度条件下的弱起伏区中的高斯波束传播问题。在此基础上，国内一些学者［8－9］根据 ITU －R 大气结构常数模型，将水平传输下的适用从弱起伏区到强起伏区的修正Rytov方法扩展到斜程传输，得到大气湍流下，激光波束斜程传输的闪烁指数变化规律。

因此，在设计激光斜程通信系统链路时，必须充分考虑大气湍流，特别是中等强度以上大气湍流对通信系统传输误码率的影响。本文在以往的研究基础上，研究大气湍流下激光斜程通信误码率的计算方法，讨论通信误码率随不同系统参数的变化规律。

2 斜程信道的光强闪烁效应

在实际激光通信系统中，从发送端出来的激光经准直后，可以作为平面波来处理。而对于平面波的斜程传播问题，一般认为在考虑了大气结构常数随高度的变化和斜程大气结构常数对相关长度的影响后，可以将水平传输的Rytov方法应用于斜程传输［10］。在弱起伏情况下，Rytov方法的闪烁指数可以表示为［8，9］:

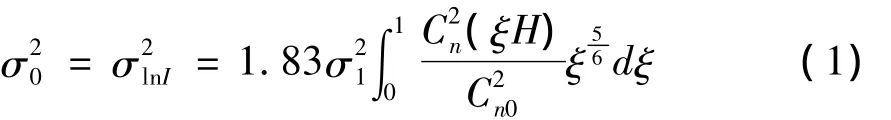
其中，σ2lnx，σ2lny分别为修正Rytov理论中大、小尺度湍流的对数振幅起伏方差。若不考虑内尺度，则平面波斜程传输的大、小尺度对数振幅方差可以分别表示为:

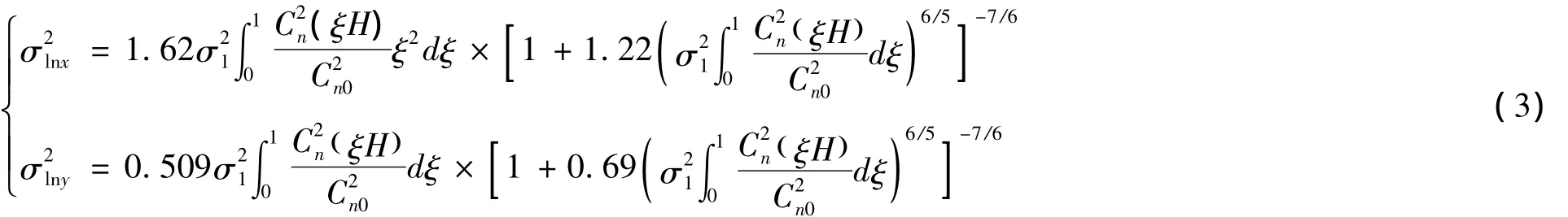
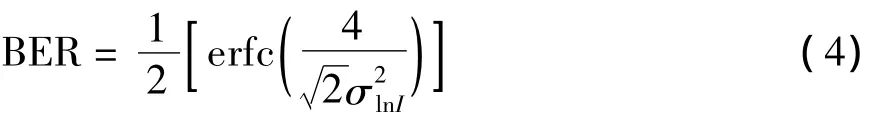
显然，将式(2)、(3)代入式(4)，就可以得到湍流条件下系统误码率的数学计算模型。

3 数值计算与分析

由式(3)可知，C2n廓线在很大程度上决定了对数振幅起伏方差σ2lnI的大小。由于C2n廓线在自适应光学、光干涉测量、光通信、激光传输等领域都有重要的应用，20世纪70 年代起，Wyngaar、Hufnagel、Abahamid等学者［11］先后总结了不同地区不同高度的C2n廓线，考虑到模拟计算的一般性，这里采用国际电信联盟提出的ITU－R湍流大气结构模型［12］，它可以表示为:

大气湍流引起的光强起伏，使得接收到的光强产生随机变化，忽大忽小，这将导致通信误码率增大，严重影响自由空间无线激光通信系统的性能。而通信系统误码率与对数振幅起伏方差的关系可以表示为［2］:

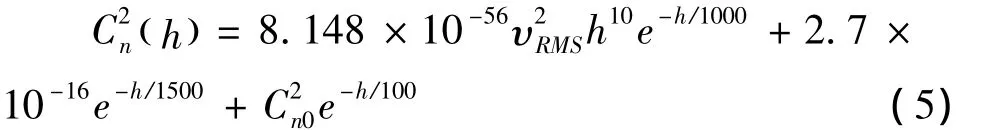
其中，υRMS表示垂直路径风速，其与近地面风速υg的

不同近地面大气结构常数、不同风速条件下，利用式(6)计算出的C2n随高度h变化的关系曲线如图1所示。从图中可以看出，在ITU－R湍流大气结构模型中，1 km高度以下，C2n的大小主要依赖于C2n0，基本不受风速υRMS的影响，随着高度的增加，C2n逐渐减小，同时受C2n0影响也逐渐减弱;当高度达到1 km以上，C2n0对C2n的大小基本没有影响;当高度达到约4 km以上，风速υRMS对C2n的影响很明显。关系可以表示为

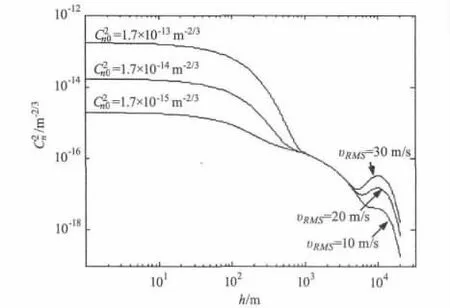
图1 不同风速和近地面大气结构常数下大气结构常数随高度的分布

结合式(3)、式(4)和式(5)，可以计算出不同的近地面大气结构常数条件下，激光斜程通信系统误码率随通信高度的变化规律，计算中近地面大气结构常数C2n0分别取三个典型值1．7 ×10－15m－2/3(弱湍流)、1．7 × 10－14m－2/3(中等湍流)、1．7 × 10－13m－2/3(强湍流)，计算结果如图2所示。可以看出，在系统其他参数不变的情况下，随着通信高度的不断增加，误码率总体上先是急剧增大，然后趋于平稳。对于C2n0=1．7 × 10－13m－2/3，在工作波长 λ =0．488μm 、天顶角θ=π/4、风速υRMS=30m/s条件下，通信高度达到1 km时，大气湍流引起的通信误码率即上升到10－8，而通常要求激光通信系统误码率在10－9以下［9］，可见，强湍流条件下，激光通信系统的有效通信高度受到严重制约，且随着湍流强度的增大，通信的有效高度将逐渐减小。此外，近地面大气结构常数对误码率具有明显的影响，当地面大气结构常数不同时，误码率进入平稳变化的高度也不同。

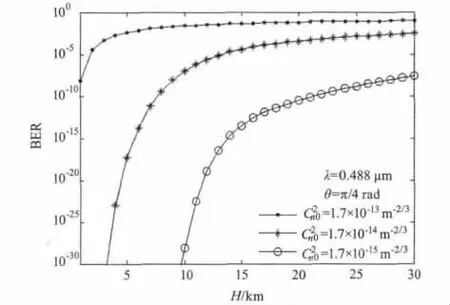
图2 系统误码率随通信高度的变化规律

图3 给出了不同的近地面大气结构常数条件下，系统误码率随天顶角的变化规律。可以看出，在同一通信高度条件下，由于激光实际传输距离随着天顶角的增加而增大，通信误码率也随之提高。而在一定的通信误码率条件下，随着湍流强度的增大，同一高度的空中平台的激光通信系统在地面上的通信覆盖范围将越来越小，即地面有效通信覆盖范围将受到湍流强度的制约。并且，近面大气结构常数越小，天顶角对通信误码率的影响也就越大。

工作波长也对通信误码率有很大影响，图4给出了不同的近地面大气结构常数条件下，系统误码率随工作波长的变化规律。可以看出，随着工作波长增长，通信误码率降低，即在一定的通信误码率条件下，通信系统的工作频率范围将受到湍流强度的制约。并且，波长越长，误码率随波长变化越明显。近面大气结构常数越小，工作波长对通信误码率的影响也就越大。

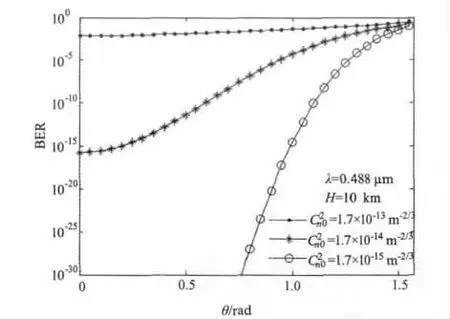
图3 系统误码率随天顶角的变化规律

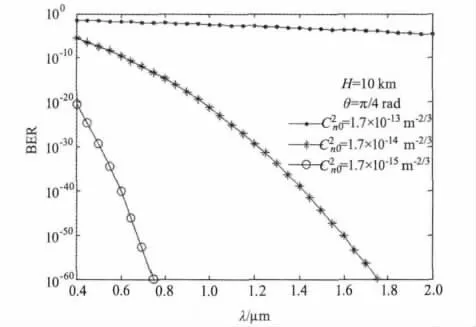
图4 系统误码率随工作波长的变化规律

此外，如前文所述，在ITU－R湍流大气结构模型中，当高度达到4 km以上，风速υRMS对大气结构常数有明显影响，因此，当通信高度在4 km以上，风速也是通信误码率的一个影响因素。图5给出了不同的近地面大气结构常数条件下，系统误码率随风速的变化规律。可以看出，相比于前面几种参数，风速对通信误码的影响较小。对于强湍流，风速大小对误码率几乎没有影响，中等湍流时，误码率随风速的增大而增大，但变化比较缓慢，而弱湍流时，随着风速的增大，误码率变化较为明显。

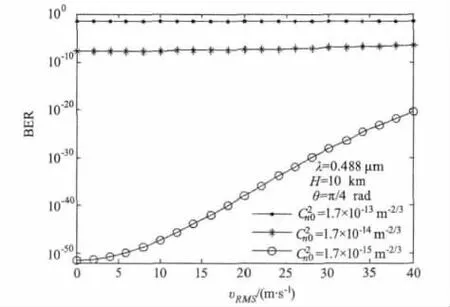
图5 系统误码率随风速的变化规律

4 结论

本文针对地空激光通信的实际情况，将修正Rytov方法应用于大气湍流条件下的光波斜程传输研究。基于ITU－R大气结构常数模型，建立了湍流条件下系统误码率的数学计算模型，对不同强度湍流信道的系统误码率进行了数值计算。数值计算结果表明:(1)大气湍流强度是影响系统性能的决定性因素;(2)在相同强度湍流条件下，系统的误码率随通信高度增加而增大，随天顶角提高而增大，随工作波长的增长而减小，随风速的增大而增大。这些，可为自由空间激光通信的工程应用提供一定的理论分析和性能预测依据。

［1］ HAO Botao，TONG Shoufeng． Receiving combination technology with detector array for spatial optical communication［J］．Laser＆ Infrared，2013，43(5):487 －490．(in Chinese)郝博涛，佟首峰．空间激光通信探测阵列接收合并技术［J］．激光与红外，2013，43(5):486 －490．

［2］ WANG Defei，CHU Zhenfeng，REN Zhenglei，et al．Influece of atmospheric turbulence on BER of laser communication system［J］．Laser ＆ Infrared，2011，41(4):390 －393．(in Chinese)王德飞，楚振峰，任正雷，等．大气湍流对激光通信系统误码率影响的研究［J］．激光与红外，2011，41(4):390－393．

［3］ Tatarskii V I．Wave propagation in a turbulent medium［M］．New York:McGraw － Hill Book Company，Inc，1961．

［4］ Chernov L A．Wave propagation in a random medium［M］．New York:McGraw － Hill Book Company，Inc，1960．

［5］ Andrews L C，Phillips R L，Hopen C Y，et al．Theory of optical scintillation［J］．J．Opt．Soc．Am．，1999，16(6):1417－1429．

［6］ Guo Lixin，Luo Zhimin，Wu Zhensen．A study of optical scintillation in the atmospheric turbulence by usingmodificationmodification of the Rytov method［J］．Chin．J of Electronic，2001，10(3):300 －304．

［7］ Andrews L C，Phillips R L，Yu P T．Optical scintillations and fade statistics for a satellite communication system［J］．Appl．Opt．，1995，34(33):7742 －7751．

［8］ WU Zhensen，LUO Zhimin，GUO Lixin，et al．Study on the scintillation of optical wave propagation in the slant path through the atmospheric turbulence［J］．Chinese Journal of Radio Science，2002，17(3):254 －257．(in Chinese)吴振森，骆志敏，郭立新，等．湍流大气中光波闪烁的斜程问题研究［J］．电波科学学报，2002，17(3):254－257．

［9］ YIXiuxiong，GUO Lixin，WU Zhensen．Study on the optical scintillation for Gaussion beam propagation in the slant path through the atmospheric turbulence［J］．Acta Optica Sinica，2005，25(4):433 －438．(in Chinese)易修雄，郭立新，吴振森．高斯波束在湍流大气斜程传输中的闪烁问题研究［J］．光学学报，2005，25(4):433－438．

［10］ Beran M J，Whitman A M．Scintillation index calculation using an altitude － dependent structure constant［J］．Appl．Opt．，1988，27(11):2178 －2182．

［11］ WANG Hongshuai，YAO Yongqiang，LIU Liyong．A review of atmospheric optical turbulence modeling research［J］．Progress of Astronomy，2012，30(3):362 － 377．(in Chinese)王红帅，姚永强，刘立勇．大气光学湍流模型研究进展［J］．天文学进展，2012，30(3):362 －377．

［12］ITU－R Document3J/31 － E．On Propagation data and prediction methods required for the design of space－toearth and earth－to－space optical communication systems［R］．Budapest:Radio Communication Study Group Meeting，2001．