基于端元优化的非线性高光谱分解算法

唐晓燕，高 昆，刘 莹，倪国强

(1．北京理工大学光电学院，光电成像技术与系统教育部重点实验室，北京100081;2．南阳理工学院电子与电气工程学院，河南南阳473004)

1 引言

由于地面的复杂多样性及传感器空间分辨率的限制，高光谱图像上存在大量混合像元，它不仅影响了基于高光谱图像的地物识别精度，而且已经成为高光谱遥感向定量化方向深入发展的主要障碍［1－2］。

高光谱图像可以利用混合像元光谱分解技术来估计组成混合像元的端元比例(丰度)。混合像元光谱分解模型可分为两类:线性光谱混合模型和非线性光谱混合模型。线性光谱混合模型假设一个光子只看到一种物质，像元的光谱是各个端元的线性组合［3］。双线性光谱混合模型在线性模型的基础上做了改进，将两种物质之间的散射作为乘积项加入线性模型［4－5］，提高了模型的精度。

对于非线性混合模型的光谱分解是个很具挑战性的问题。几乎所有的基于非线性模型的解混算法都是采用最小二乘估计［4，6］。近来一些学者提出了基于支撑向量回归［7］和神经网络［8］的非线性分解方法。Halimi等［4］采用分层贝叶斯算法来估计广义双线性模型(Generalized Bilinear Model，GBM)的丰度系数和噪声变量，取得了较好的结果，但是该算法是利用所有的端元来进行计算的。自然界地物分布的复杂性导致了高光谱图像通常是非均质的，例如背景不单一、地物空间分布不均匀，较高的地物存在的阴影影响等。本文针对非均质背景下，混合像元中包含的端元种类一般是不相同的［9］，且当端元中包含高度较高的地物类型时，高光谱图像中不可避免受到阴影的影响，导致光谱分解精度下降，利用端元的可变性，对基于分层贝叶斯模型非线性光谱分解算法进行改进，加入阴影端元对混合像元端元集进行优化，用优化端元子集采用基于分层贝叶斯模型的非线性光谱分解算法来获取相应端元的丰度。

2 基于分层贝叶斯模型参数估计的双线性混合模型

基于贝叶斯推理方法进行参数估计的基本思路［10］是基于观测样本、参数的先验分布与似然函数，对所研究的对象或问题建立参数后验分布的概率模型(Bayesian模型)。

2．1 广义双线性模型

广义双线性混合模型［4］如式(1)所示:

其中，y∈RL为每个像元的光谱列向量，L为谱段数。端元光谱 mk=k=1，2，…，R 。α =是每个端元在像元点y中所占的丰度分数向量，n= [n1，n2，…，nR]T是附加的白噪声，通常假设其为独立的，且服从0均值方差为σ2的高斯分布，n ～ Ν(0L，σ2IL)，IL是L×L矩阵。

2．2 似然估计

式(1)的观测模型和噪声n的高斯参数满足:

2)非线性参数先验分布:由于丰度之间的相互作用通常是小于单个丰度值，参数γi，j被假设是非负的且小于1。γi，j没有其他信息，因此被假设满足［0，1］之间的均匀分布［11］。

3)噪声方差的先验分布:通常假设σ2的先验服从共轭逆 Gamma分布［12］:

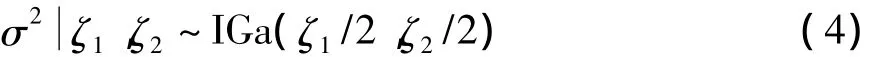
||·||指的是标准l2范数。y为高光谱图像中一个像元的光谱向量，是已知的数据，未知参数向量θ=(αT，γT，σ2)T。下面介绍根据分层贝叶斯模型估计GBM 的未知参数向量 θ =(αT，γT，σ2)T。

2．3 参数先验分布

1)丰度先验分布:丰度的和为1约束可以表示为一个端元的丰度αk*是其他端元丰度的函数，如式(3)所示。由于没有该参数的其他信息，αk*的先验选择的是Sk*统一分布。

其中，ζ1和 ζ2为两个超参数。设ζ1=2 ，ζ2=ζ，可得到一个可调的超参数ζ。

4)超参数先验分布:超参数ζ对分解的精度影响很大，其先验分布利用Jefffery无信息先验原则确定为:

2．4 θ的后验分布

参数向量θ的联合后验概率分布可用下面公式来计算:

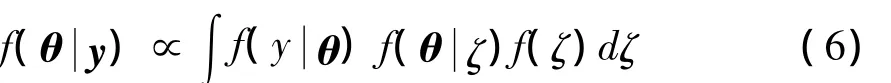
其中，∝表示“成正比例”，f(θζ)是式(2)定义的似然函数。假设所有参数是先验独立的，则f(θζ)

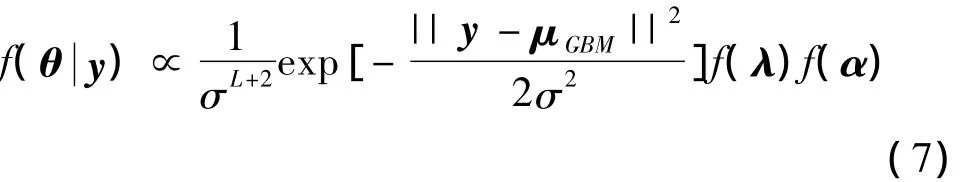
因为f(α)需满足和为1和非负约束，用最小均方根误差和最大先验估计结合的后验分布并不容易确定。

2．5 基于MCMC的参数估计

MCMC的基本思想是构建一条马尔科夫链，使其平衡分布为P，然后对这条马尔科夫链模拟并对其平衡分布采样。而GibbS抽样方法是最简单的MCMC方法，适用于条件概率分布容易计算的情况。，代入式(6)可得到 θy的后验分布:它依据所有其他变量的当前值，对其中每一个变量进行迭代抽样。经过一段时间的迭代后，可以认为时刻x(t+k)的边缘分布趋向平稳，此时它收敛，而在收敛出现前的Nbi次迭代中，由于初值的影响，各状态的边际分布还不能认为是P(x1，x2，…，xl)。因此在估计期望时，应该把前Nbi次迭代舍去。

为了获得对参数 θ =(αT，γT，σ2)T的估计，从待估参数的后验分布来抽样估计。根据Gibbs采样，很容易产生 NMC个采样，Xθ={σ2(t)，α(t)k*，γ(t)}t=1，…，NMC。这些采样逐渐接近式(7)中所示的联合后验分布，形成的马尔科夫链的统计分布为f。结果，这些参数可经验的采用最后Nr=NMC－Nbi个采样值的均值来计算。

其中，x为感兴趣的参数。

3 基于端元优化的非线性光谱分解算法

已有的最小二乘算法和基于分层贝叶斯模型的非线性光谱解混算法，均假设图像中所有像元内包含的端元种类是相同的，即利用所有的端元组成的端元矩阵对影像中混合像元进行光谱分解。然而，混合像元中包含的端元种类一般是不相同的。实际上，只有在多种地物的交界处的像元才可能包含多数或者全部的端元种类。而且，当端元中包含高度较高的地物类型时，高光谱图像中不可避免地会出现阴影。本文利用端元的可变性，加入阴影端元对混合像元端元集进行优化，并用对优化的端元子集利用分层贝叶斯模型进行丰度估计。算法的具体步骤如下:

1)对于图像 Y= ［y1，y2，…，yN］，根据初始端元集 M= ［m1，m2，…，mp］，利用分层贝叶斯模型计算每个像元的丰度向量α和非线性系数γ;

2)计算每个像元的重建误差(Reconstruction Error，RE)，对 RE 利用 Ostu 算法［13］进行阈值分割，获得误差较大的像元点集;

3)对误差较大的点yi，对丰度向量α中的元素由大到小进行排序，确定排序后的丰度向量为α珘=［，…］，该排序结果对应于端元对该混合像元的贡献大小;

5)对 αs重新计算 REs，如果 REs＜RE，就接受αs;否则保留原来的α。

4 实验结果

本文采用模拟数据和圣地亚哥机场真实数据来对提出的算法进行验证。为了验证算法的有效性，采用全约束的最小二乘算法(Fully Constrained Least Square，FCLS)和基于分层贝叶斯估计GBM的算法与本文提出优化端元的GBM(Optimal Endmembers GBM，OE－GBM)进行对比。试验结果采用估计丰度和实际丰度的丰度均方根误差［14］(A-bundance RootMean Square Error，ARMSE)，像元光谱估计值和实际值的重建误差和光谱角分布［15］(Spectral Angle Map，SAM)来对各算法进行评价，具体计算公式如式(9)～(11)。这三个参数越小代表算法效果越好。

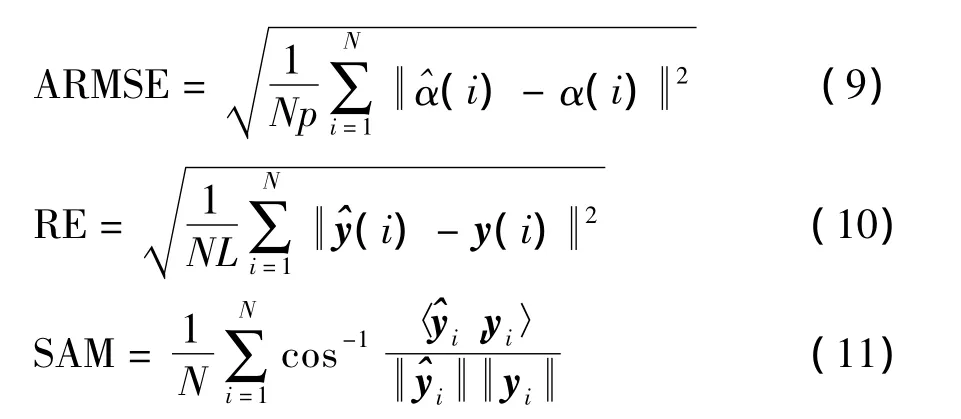
4．1 模拟数据实验

在ENVI软件自带的光谱库中抽取三种纯物质:沥青、路、树，根据AVIRIS高光谱图像首先进行重采样得到220个谱段，然后去除水汽吸收和高噪声谱段，剩余162个谱段用于生成两幅模拟数据。图像 I1采用 LMM 模型，α1，α2，α3满足［0，1］直接的均匀分布，且满足和为1约束，从中随机选取10%的点，用阴影端元代替某个端元。图像I2采用GBM 模型，参数 α1，α2，α3满足［0，1］之间的均匀分布，且满足和为 1 约束，非线性系数 γ1，2，γ1，3，γ2，3满足［0，1］之间的均匀分布，从中随机选取10%的点，用阴影端元代替某个端元。图像I1和I2都加入方差σ2=3．0×10－4的高斯噪声。模拟图像的产生模型和参数如表1所示。

表1 模拟图像的产生模型和参数

预热的迭代次数Nbi=300，迭代次数Nr=700，用式计算参数估计值。对比FCLS、GBM和本文提出的OE－GBM算法的效果。表2给出了不同算法分解两幅图像的重建误差(RE)和光谱角分布(SAM)和丰度均方根误差(ARMSE)。对于图像I1，OE－GBM算法得到了最小RE、SAM和ARMSE，效果最好。由于图像I1是采用线性混合，因此FCLS的解混效果优于GBM。对于图像I2，OE－GBM算法的RE、SAM和ARMSE也优于其它两种FCLS和GBM算法。每幅图像比较合适的算法是采用相应模型解混的算法。但是，也可看出，采用本文提出OE－GBM算法对于各种模型产生的图像，均有较好的解混效果。

表2 解混算法的性能比较

表3给出了用实际端元进行解混时两幅模拟图像所需的计算时间，时间的单位为秒。实验采用的计算机硬件环境为Inter Core i3双核CPU 3．07GHz，内存2GB，软件环境为 Microsoft Windows 7、MATLAB 2012(b)。根据表3所示，FCLS解混算法所需时间最少，本文提出的OE－GBM算法所需时间与GBM算法解混所需时间相当。

表3 用实际端元进行解混的计算时间(s)

4．2 真实数据实验

真实数据实验采用美国圣地亚哥机场的AVIRIS数据。波长为0．389～2．467μm，除去低信噪比和水吸收谱段(谱段1 －2，104－113，148－167，221－224)，后剩余188个谱段数据。为了减少计算的时间复杂度，从原始图像中截取大小为50×50的子图(如图1所示)。从图1可看出，端元数目为4，分别是:飞机、混凝土1、混凝土2、硬土。由于相同地物光谱的可变性，4种端元的参考光谱本文从图中人工获得，例如飞机的参考光谱，从飞机机身的中心位置抽取4个像元，求其光谱的均值作为飞机的参考光谱。

图1 圣地亚哥机场的伪彩色图像(R:谱段90;G:谱段50;B:谱段27)

用OE－GBM、FCLS、GBM三种算法进行解混得到的RE图像如图2所示。从图2中可看出，GBM解混算法的RE优于FCLS，但是由于光照的不均匀和阴影的影响，在飞机区域的误差较大。OE－GBM算法考虑了阴影端元，且对参与分解的端元集做了优化，因此RE小于FCLS和GBM算法。

图2 圣地亚哥机场真实值解混的重建误差(RE)

5 结论及讨论

本文针对非均质背景下，混合像元中包含的端元种类一般是不相同的，且当端元中包含高度较高的地物类型时，高光谱图像中不可避免会受到阴影的影响，导致光谱分解精度下降，利用端元的可变性对基于分层贝叶斯模型的双线性光谱解混算法进行改进。加入阴影端元对混合像元的端元集进行优化，并用优化端元子集采用基于分层贝叶斯模型的双线性光谱解混算法进行光谱解混，实验结果表明，提出的OE－GBM算法能很好的解决高光谱图像中存在的阴影，光谱分解效果优于 FCLS和 GBM算法。

［1］ TONG Qingxi，ZHANG Bing，ZHENG Lanfen．Hyperspectral remote sensing［M］．Beijing:Higher Education Press，2006．(in Chinese)童庆禧，张兵，郑兰芬．高光谱遥感——原理、技术与应用［M］．北京:高等教育出版社，2006．

［2］ GAO Xiaojian，GUO Baofeng，YU Ping．Classification of hyperspectral remote sensing image based on spatialspectral integration［J］．Laser ＆ Infrared，2013，43(11):1296 －1300．(in Chinese)高晓健，郭宝峰，于平．高光谱空谱一体化图像分类研究［J］．激光与红外，2013，43(11):1296 －1300．

［3］ Dobigeon N，Tourneret J，Richard C，et al．Nonlinear unmixing of hyperspectral images:Models and algorithms［J］．IEEE Signal Processing Magazine，2014，31(1):82－94．

［4］ FANWenyi，HU Baoxin，Miller J，etal．Comparative study between a new nonlinearmodel and common linearmodel for analysing laboratory simulated－forest hyperspectral data［J］．International Journal of Remote Sensing，2009，30(11):2951－2962．

［5］ Halimi A，Altmann Y，Dobigeon N，et al．Nonlinear unmixing of hyperspectral images using a generalized bilinearmodel［J］．IEEE Transactions on Geoscience and Remote Sensing，2011，49(11):4153 －4162．

［6］ Combe JP，Launeau P，Carrère V，et al．Mapping microphytobenthos biomass by non－linear inversion of visible－ infrared hyperspectral images［J］．Remote Sensing of Environment，2005，98(4):371 －387．

［7］ WU Bo，ZHANG Liangpei，LIPingxiang．Unmixing hyperspectral imagery based on support vector nonlinear approximating regression［J］．Journal of Remote Sensing，2006，10(3):312 －318．(in Chinese)吴波，张良培，李平湘．基于支撑向量回归的高光谱混合像元非线性分解［J］．遥感学报，2006，10(3):312 －318．

［8］ Liu W G，Wu E Y．Comparison of non －linear mixture models:sub － pixel classification［J］．Remote Sensing of Environment，2005，94(2):145 －154．

［9］ Rogge D M，Rivard B，Zhang J，et al．Iterative spectral unmixing for optimizing per － pixel endmember sets［J］．IEEE Transactions on Geoscience and Remote Sensing，2006，44(12):3725 －3736．

［10］ CHEN Yajun，LIU Ding，LIANG Junli．Bayesian inference on parameters formixtures ofα－stable distributions based on markov chainmonte carlo［J］．Journal of Xi＇an University of Technology，2012，28(4):385 －391．(in Chinese)陈亚军，刘丁，梁军利．基于MCMC的混合α稳定分布参数贝叶斯推理［J］．西安理工大学学报，2012，28(4):385－391．

［11］ Somers B，Cools K，Delalieux S，et al．Nonlinear hyperspectralmixture analysis for tree cover estimates in orchards［J］．Remote Sensing of Environment，2009，113(6):1183－1193．

［12］ Dobigeon N，Tourneret JY，Chang C I．Semi－ supervised linear spectral unmixing using a hierarchical Bayesian model for hyperspectral imagery［J］．IEEE Transactions on Signal Processing，2008，56(7):2684 －2695．

［13］ Otsu N．A threshold selectionmethod from gray－levelhistograms［J］．Automatica，1975，11(285 －296):23 －27．

［14］ Plaza J，Plaza A，Pérez R，et al．Joint linear/nonlinear spectral unmixing of hyperspectral image data［C］//IEEEGeoscience and Remote Sensing Symposium，2007:4037－4040．

［15］ Keshava N，Mustard JF．Spectral unmixing［J］．IEEE Signal Processing Magazine，2002，19(1):44 －57．