股骨干骨折锁定板内固定治疗的有限元分析
董巍,路博,石向明,徐秀霞,徐晓磊,王增立*
(1.中国石油天然气集团公司中心医院骨科,河北 廊坊 065000;2.中国石油天然气集团公司中心医院放射科,河北廊坊 065000;3.中国石油天然气集团公司中心医院核医学科,河北 廊坊 065000)
近年来,随着现代化交通运输工具的普及,临床工作中面临着越来越多的高能量损伤导致的股骨干骨折。在股骨干骨折的治疗方法中,锁定板由于具有成角稳定性、手术中无需预弯塑形、可保护骨折端血运等优点,越来越受到重视。但对于锁定板治疗股骨干骨折过程中如何选择螺钉位置及数量,尚缺乏有针对性的分析研究。有限元分析方法可以对锁定板治疗股骨干骨折进行深入的力学分析。近年来,CT检查由于能够精确的描述骨组织的几何外形和组织特性,因而被广泛应用于骨组织有限元建模[1,2]。
本研究基于有限元分析前处理软件MIMICS、Solidworks及有限元分析软件ABAQUS,建立锁定板治疗股骨干骨折的有限元模型,并模拟不同螺钉固定位置情况下,锁定板及螺钉最大应力变化情况,为锁定板治疗股骨干简单骨折的临床应用提供理论指导。
1 资料与方法
1.1 一般资料 选择健康志愿者23名,其中男15名,女8名;年龄28~79 岁,平均(56.70±13.20) 岁。入选标准:a)既往无股骨骨折病史;b)无双下肢神经肌肉疾病;c)可正常行走完成日常生活各项活动。
1.2 方法 志愿者取仰卧位,从骨盆至膝关节进行CT扫描(西门子Biography true point 64层螺旋CT),采集左股骨数据,将数据以DICOM格式导入MIMICS 10.01软件(Materialise公司,比利时),建立骨骼3D模型,依据CT灰度值由MIMICS为骨骼模型自动赋材料属性。
用三坐标测量仪扫描锁定板,并生成点云文件,Solidworks 2010(SolidWorks公司,美国)生成曲面及实体文件。因锁定螺钉细小螺纹结构将大幅增加运算量,且简化后对分析结果无明显影响,故用同直径圆柱体模拟,并通过ABAQUS 6.10(DASSAULT SIMULIA公司,法国)设置“Tie”约束模拟“钉-板”及“钉-骨”间锁定功能。用ABAQUS于股骨中段处制造一宽约1 mm间隙模拟简单骨折,骨折端间设置接触;或于股骨中段处制造一宽约6 mm间隙,模拟粉碎性骨折[3]。ABAQUS为锁定板及锁定螺钉依据钛金属物理性质赋材料属性(弹性模量110GPa,泊松比0.3)。
将锁定板两侧钉孔分别从外向内依次标记为1至6,即最靠近两端钉孔为1,最靠近中心钉孔为6,每次选择不同钉孔进行螺钉固定,模拟5种不同固定方式(见表1)。23 例股骨均进行上述2种骨折模型及5种不同固定方式下数据采集。
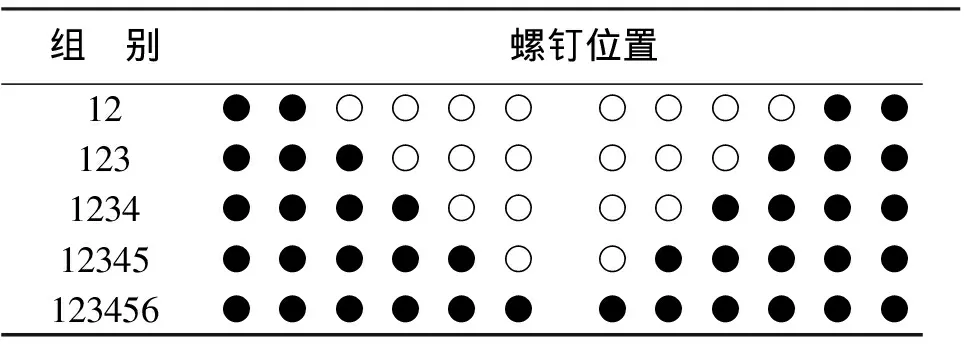
表1 各组螺钉位置
ABAQUS进行装配并划分网格,股骨及锁定板为不规则形状,故采用10节点四面体单元(C3D10),锁定螺钉以规则圆柱体模拟,故采用8节点六面体单元(C3D8)。股骨远端节点约束所有自由度,模拟固支边界条件;股骨头顶端施加350 N垂直向下的压力,模拟正常人站立时股骨所受外力。
1.3 统计方法 采用配伍组设计的方差分析方法进行统计,检验水准α=0.05,P<0.05为有统计学意义。采用最小显著性差异法(LSD)法对各组数据间进行两两比较,检验水准α=0.05,P<0.05为有统计学意义。
2 结 果
通过使用MIMICS、Solidworks及ABAQUS软件,可建立股骨骨折及锁定板内固定模型,并对其进行有限元分析,得出在压力作用下股骨骨折锁定板内固定模型的应力云图和各向形变。
不同固定方式下的锁定板及螺钉上最大应力值均出现在最内侧螺钉处,即最靠近骨折线的螺钉处。对于简单骨折,其最大值随着最内侧螺钉的外移而逐渐减小(见图1);对于粉碎性骨折,其最大值随着最内侧螺钉的外移而逐渐增大(见图2)。通过对测量结果进行方差分析,对于简单骨折和粉碎性骨折,其组间差异均有统计学意义(P<0.05)。对所得结果进一步两两比较可知,对于简单骨折,除12和123两组外,任意两组间差异均有统计学意义(P<0.05)(表2);而对于粉碎性骨折,任意两组间差异均有统计学意义(P<0.05)(见表3)。

图1 简单骨折锁定板及螺钉最大应力值变化情况

图2 粉碎性骨折锁定板及螺钉最大应力值变化情况
3 讨 论
有限元分析是一种数值分析方法,其基本原理是将一个由无限个质点构成且有无限个自由度的连续体划分为有限个小单元体所组成的集合体。单元之间通过节点相连,相互作用力通过节点传递。当每个单元的物理特性及节点载荷、边界条件明确后,通过节点位移与节点力之间的关系式、可计算出每个单元的刚度矩阵,各个单元的刚度矩阵集合成构件的总刚度矩阵,并通过数学形式表达。随着数字医学的兴起,计算机技术和生物力学的发展,有限元技术在骨科领域得到广泛应用[4-7]。近年来,伴随着技术的进步,有限元分析已经由过去对生物体结构的简单模拟和近似计算,发展到能对人体各部分复杂的非均质性结构进行高相似度模拟和精密分析,成为现代人体生物力学研究的重要工具。在骨科方面应用更为广泛,已经涉及脊柱、关节、颅底、韧带、骨盆、假体等领域[8-10]。尤其在分析骨与内固定物之间的关系,比较各种手术方式[11,12]方面,发挥了不可替代的作用。
表2简单骨折锁定板及螺钉最大应力平均值两两比较结果
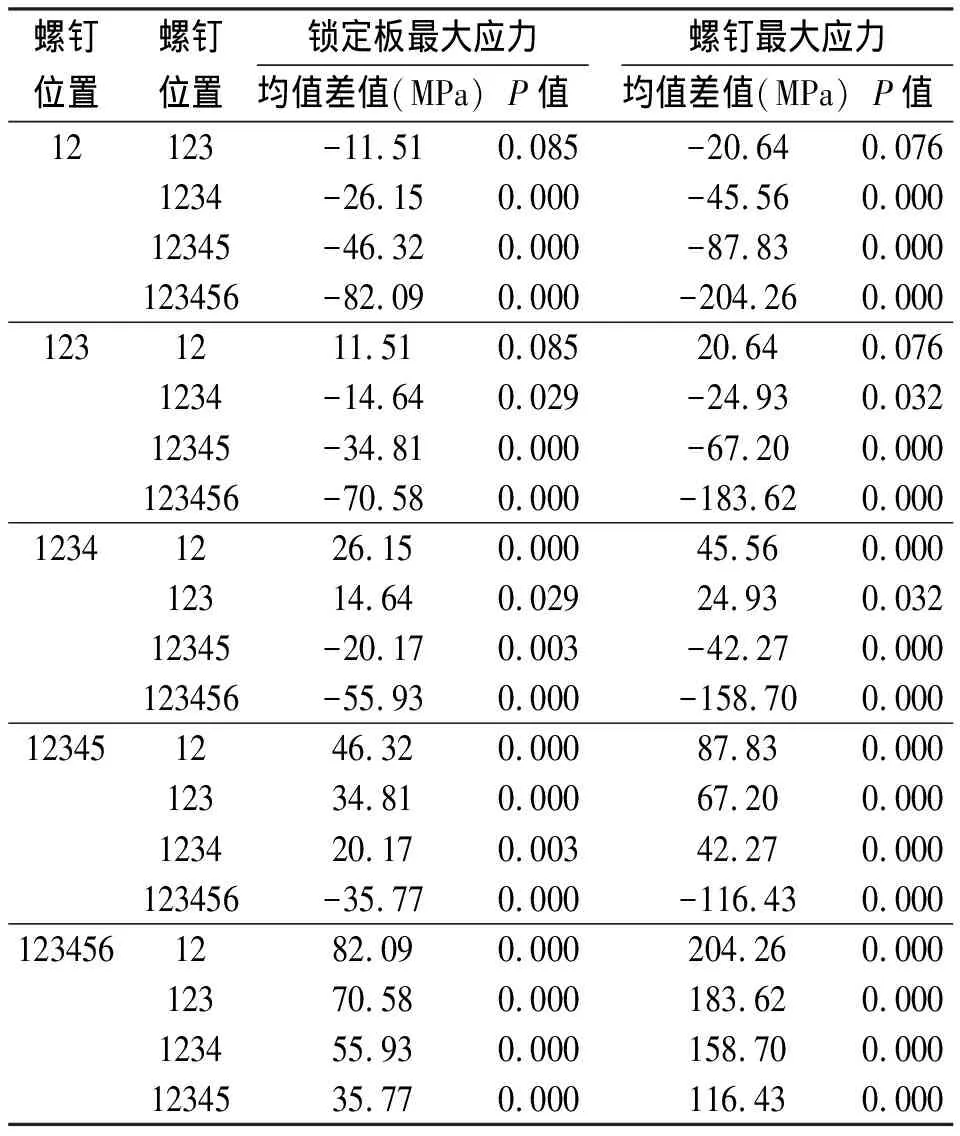
(MPa)P(MPa)P12123-11.510.085-20.640.0761234-26.150.000-45.560.00012345-46.320.000-87.830.000123456-82.090.000-204.260.0001231211.510.08520.640.0761234-14.640.029-24.930.03212345-34.810.000-67.200.000123456-70.580.000-183.620.00012341226.150.00045.560.00012314.640.02924.930.03212345-20.170.003-42.270.000123456-55.930.000-158.700.000123451246.320.00087.830.00012334.810.00067.200.000123420.170.00342.270.000123456-35.770.000-116.430.0001234561282.090.000204.260.00012370.580.000183.620.000123455.930.000158.700.0001234535.770.000116.430.000
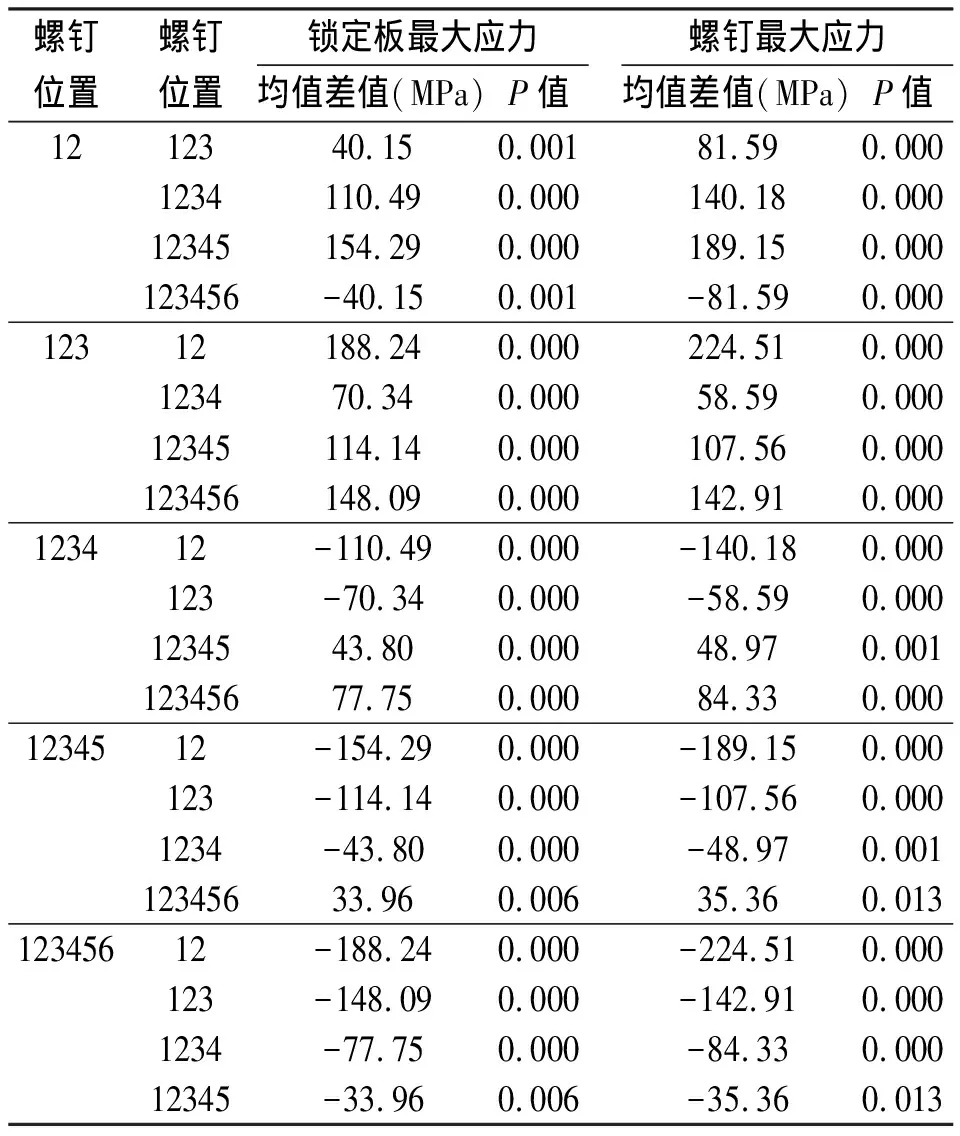
表3 粉碎性骨折锁定板及螺钉最大应力平均值两两比较结果
传统有限元方法通常将骨组织简单区分成皮质骨和松质骨,分别赋予弹性模量和泊松比等材料属性后进行分析。然而,由于骨骼并非单一均质材料,即使单纯皮质骨的不同部位也有不同属性区别,因此传统方法在对骨组织材料属性的模拟上存在很大的简化,无法体现不同个体之间的区别。本研究通过MIMICS软件精确再现股骨外形,并依据CT值对股骨赋材料属性,从而避免传统方法赋材料属性所造成的误差,使有限元分析结果更加精确。通过采集23 例不同年龄志愿者的股骨数据,并分别模拟多次不同方式的锁定板内固定,有效避免了单次模拟条件下内固定位置偏移所引起的误差,使所得出的结论更具有可重复性。
通过本研究结果可知,对于股骨干简单骨折,采用锁定板内固定,随着最内侧固定螺钉的外移,锁定板及螺钉上分布的最大应力均逐渐减小,但减小的趋势逐渐变缓。最大应力的逐渐减小是由于加载作用力后,锁定板将发生弹性形变,从而使骨折端两侧互相接触,阻止了锁定板进一步发生形变,且随着锁定板中间无螺钉区域的逐渐延长,应力可以在更大范围内分布,从而使最大应力减小。但这种应力逐渐减小的趋势呈逐渐变小的趋势,每侧2枚螺钉固定与每侧3枚螺钉固定比较,两者间无统计学差异。对于股骨干粉碎性骨折,随着最内侧固定螺钉的外移,锁定板及螺钉上分布的最大应力均逐渐增大。这种变化趋势的产生,是由于随着加载作用力后,锁定板将发生弹性形变,但对于粉碎性骨折,因其骨折端不能产生有效传递应力的接触,故无法阻止锁定板进一步发生形变,随着锁定板中间无螺钉区域的逐渐延长,力臂相应延长,力矩增大,从而导致锁定板和螺钉上的最大应力增大。
在骨折内固定系统中,内固定物所承受的应力与其预期寿命密切相关,过高的应力将缩短其使用时限,导致内固定物折断、松动等严重后果。对于股骨干简单骨折,虽然每侧两枚螺钉比每侧3枚螺钉的固定方式有进一步减小最大应力的趋势,但为了增强内固定抗扭转强度,保证内固定的强度,选择每侧三枚螺钉进行固定是较为稳妥的方法,且应使最内侧螺钉尽量远离骨折端。对于股骨干粉碎性骨折,则应使最内侧螺钉尽量靠近骨折端。根据临床经验,锁定板上的钉孔无需全部使用螺钉固定,但为了保证粉碎性骨折内固定的抗扭转强度,每侧需保证至少4枚螺钉,且最外侧钉孔应予螺钉固定。结合本研究结果,即编号为1和6的钉孔需螺钉固定,编号2、3、4、5的钉孔可选择2~3个进行螺钉固定。若最内侧钉孔因粉碎性骨折跨度较大无法使用,则以此类推。
本研究对股骨干简单骨折的锁定板内固定进行力学分析并得出结论,此结论对于四肢长管状骨的锁定板内固定均具有一定借鉴意义,具体的结论有待于进一步的实验证实。
参考文献:
[1]Taddei F,Martelli S,Reggiani B,etal.Finite-element modeling of bones from CT data:sensitivity to geometry and material uncertainties[J].IEEE Trans Biomed Engi,2006,53(11):2194-2200.
[2]彭亮,曾小丽,白净.基于CT数据的股骨三维有限元建模方法[J].清华大学学报(自然科学版),2007,47(3):416-419.
[3]Stoffel K,Dieter U,Stachowiak G,etal.Biomechanical testing of the LCP-how can stability in locked internal fixators be controlled[J].Injury,2003,34(suppl 2):11-19.
[4]Ozan F,Yildiz H,Bora OA,etal.The effect of head trauma on fracture healing:biomechanical testing and finite element analysis[J].Acta Orthop Traumatol Turc,2010,44(4):313-321.
[5]Arabmotlagh M,Pilz M,Warzecha J,etal.Changes of femoral periprosthetic bone mineral density 6 years after treatment with alendronate following total hip arthroplasty[J].J Orthop Res,2009,27(2):183-188.
[6]Dudda M,Gueleryuez A,Gautier E,etal.Risk factors for early dislocation after total hip arthroplasty:a matched case-control study[J].J Orthop Surg(Hong Kong),2010,18(2):179-183.
[7]马信龙,付鑫,马剑雄,等.人股骨近端空间结构重建新方法及有限元模型的建立[J].生物医学工程学杂志,2011,28(1):71-75.
[8]李孝林.基于CT精细扫描构建人体胸腰段脊柱三维有限元模型的方法及意义[J].山东医药,2009,49(14):8-10.
[9]刘士明,周恩昌,张铮,等.肘关节三维有限元模型的建立及意义[J].山东医药,2009,49(27):22-23.
[10]史振满,史疆,王鑫,等.骨折髋支撑关节治疗股骨颈骨折的有限元力学分析[J].中国组织工程研究与临床康复,2010,14(13):2462-2466.
[11]Beaupre GS.Effect of fracture gap on stability of compression plate fixation:a finite element study[J].J Orthop Res,2011,29(1):152.
[12]Amin S,Kopperdhal DL,Melton LJ 3rd,etal.Association of hip strength estimates by finite-element analysis with fractures in women and men[J].J Bone Miner Res,2011,26(7):1593-1600.

