群体复合形优化算法在核动力设备优化设计中的应用

阎昌琪，李贵敬，王建军

（哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001）

目前世界大多电力市场竞争日趋激烈，电力生产商和供应商更加关注运行成本和投资的盈利能力。现有核电系统在这样的市场上显得初期投资太高、建设期太长、项目规模太大。尽管核动力在中期和远期的市场中均具有竞争潜力，但欲使这种潜力变为现实，就必须能在确保核电站运行安全的前提下大幅降低成本［1］。因此，选择一种合理的优化方法，通过寻找设计参数的最优组合，减小核动力装置重量，具有重要意义。

复合形优化算法（CA）是工程设计中较为常用的一种有约束的直接求解方法，对目标函数和约束函数的性质无特殊要求，并在核工程领域中得到了应用［2-3］。但对复杂优化问题，传统复合形优化算法（TCA）易于陷入局部最优值［4］。本文首先建立多个复合形，并基于其相似度最低原则，给出多复合形的最优化组合，增强复合形顶点的多样性，提高算法获取全局优点信息的能力，以使算法具有更佳的全局搜索能力。

1 CA原理及改进

1.1 CA基本原理

CA 的基本原理是在n 维受约束的设计空间内创建由k 个顶点构成的多面体（复合形），然后对复合形顶点的函数值逐一进行比较，不断丢弃函数值最劣的顶点，代之以满足约束条件且函数值有所改善的新顶点，如此重复，逐步逼近最优点。

CA 将目标函数值最大的顶点XH视为最坏点，除最坏点外其余顶点的中心点X0由式（1）计算得到，即：

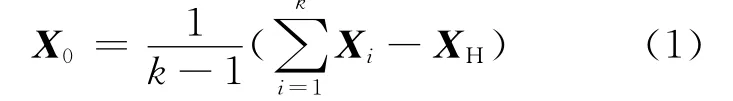
式中，Xi为复合形的各顶点。

在中心点与最坏点的连线上，利用式（2）寻找既满足约束条件，又较XH目标函数值小的顶点XR，并替换XH构成新的复合形，如此反复进行，当复合形收缩到足够小时，即可将复合形顶点中的最好点作为近似最 优 点 输 出［4-5］。

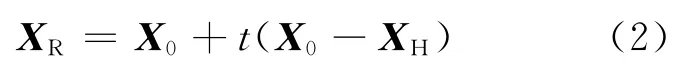
式中，t为映射系数，其初始值通常取1.3，随后不断减半收缩（t=t／2），直至寻找到改进点XR。

1.2 算法改进

CA 初始复合形的顶点个数有限，而初始顶点的生成又具有随机性，不能保证各顶点均匀覆盖可行域，因此难以保证CA 对整个搜索空间的状况有足够的了解。

针对TCA 的缺点提出以下改进方案，得到群体复合形优化算法（CCA）。

1）建立群体复合形，它由多个复合形组成。CCA 初始复合形顶点个数较TCA 有大幅提高，因而群体初始复合形对可行域空间的覆盖面明显大于TCA，从而增强了算法对可行域空间状况的了解能力，提高了算法搜索到全局最优点的概率。图1为CCA 逻辑框图。

2）群体复合形中任选1个复合形与其余复合形之间实现相似度最低的最优化组合。所谓相似度，是由两个顶点之间的海明距离表示的，海明距离越小，两顶点的相似度就越大，海明距离的计算如下：

式中：n 为顶点向量的元素个数；xim、xjm为Xi、Xj的第m 个元素。

最优化组合具体实施措施为：首先，除被选中的复合形——第α 个复合形外，其余复合形基于CA 基本寻优措施完成并行自身优化，分别收敛于自身最优复合形；其次，第α个复合形与上步优化所得到的每个自身最优复合形，形成组合优化关系，即在每个自身最优复合形中，选取与第α个复合形各顶点平均相似度最低且优良度最高的顶点，作为第α 个复合形的寻优操作基准点，优化第α个复合形，最终第α个复合形达到收敛要求后，最优顶点即为优化结果。最优化组合利用每个复合形的相对最优信息优化被选中的复合形，使第α 个复合形充分获取各复合形的相对最优信息，算法的全局搜索能力显著提高。

2 CCA性能测试

选取典型基准测试函数，测试CCA 较TCA 是否具有更佳的全局搜索能力。Schwefel函数为：

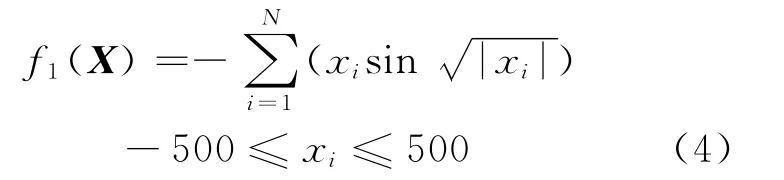
式（4）属多维连续多峰函数，可行域空间内广泛分布大量局部极值点，仅有1个全局极小点为f1（X）=-418.982 874 8 N，xi=420.968 7（i=1，2，…，N）。由于空间中存在多个局部极小点与全局极小点目标函数值较接近，且远离全局极小点，TCA 受搜索能力的限制极易收敛于次优解。为更直观地认识基准测试函数，其三维视图（N=2）示于图2a。

将TCA 和CCA 分别用于Schwefel测试函数的优化计算中，对比结果示于图2b，其中N=5。CCA 对基准函数的优化结果均分布在函数解析最优值附近，与函数解析最优值偏差很小，最大相对偏差的数量级为10-6，随机产生的25次计算结果与最优值几乎完全重合。而TCA 对Schwefel函数的优化结果散乱地分散在函数最优值的上方，最大相对偏差达49.94%，最小相对偏差为10.37%，与CCA 相比计算精度极差。结果显示：CCA 对Schwefel函数的单次优化平均时间为1.073 3s，TCA 对Schwefel函数的单次优化平均时间为0.038 2s。可见，CCA 的计算时间普遍大于TCA，但计算时间以s为单位，其实际偏差并不大。

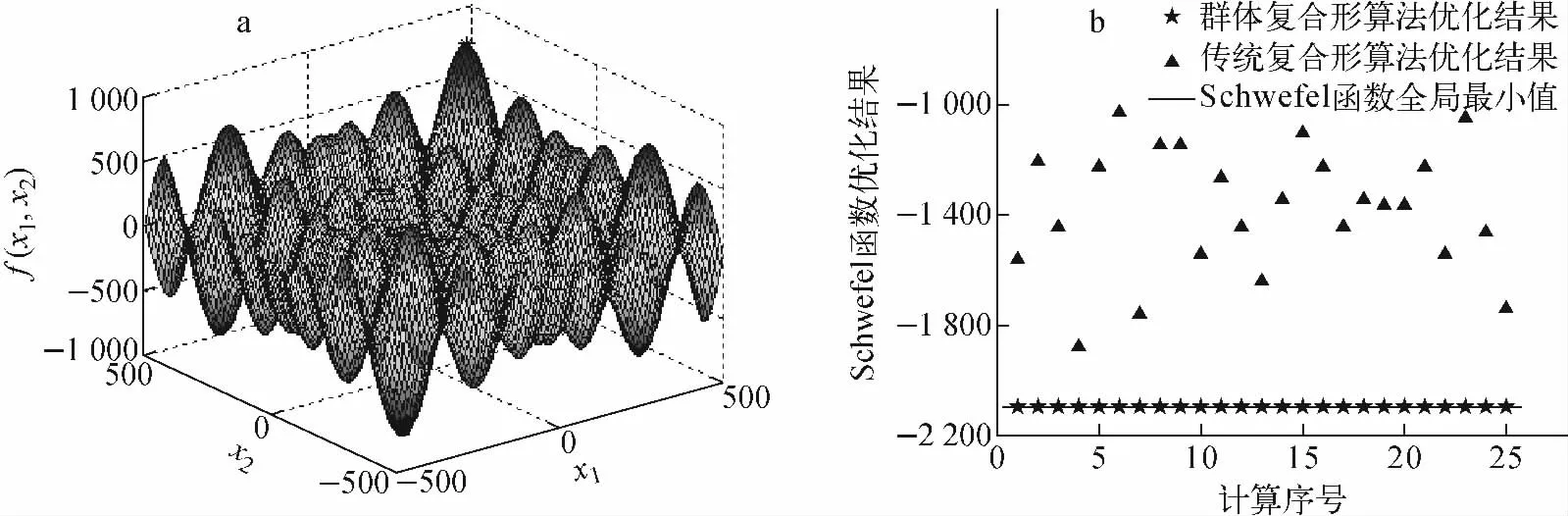
图2 Schwefel函数三维图像（N=2）（a）及CCA、TCA 对Schwefel函数优化效果对比（b）Fig.2 Three-dimensional outlooks of Schwefel function with N=2（a）and contrast between CCA and TCA optimization effect based on Schwefel function（b）

结果表明：CCA 较TCA 具有明显的优越特性，包括全局搜索能力强、收敛精度高、稳定性好。虽然计算时间略大于TCA，但其实际偏差并不明显，计算时间的增加量对优化工作无太大的影响。因此，CCA 在优化性能方面所取得的改进效果具有重要的应用价值。

3 将CCA应用于核动力设备的优化设计

本文以减小核电高压加热器重量为优化目标，基于CCA 寻求高压加热器结构参数的最佳组合。

3.1 高压加热器数学模型的建立

选取秦山300 MW 压水堆核电厂系统中的3号高压加热器为设计原型。数学模型的设计过程参见文献［6-8］，注意以下几点。

1）核电高压加热器的抽汽是饱和蒸汽，因此高压加热器仅具有凝结段和疏水冷却段，凝结段和疏水冷却段的过渡点给水温度tt（℃）依照下式［6］计算：

式中：tw1为给水入口温度，℃；hhw为加热器壳侧压力ph（MPa）下的饱和水比焓，kJ／kg；hod为疏水出口比焓，kJ／kg；qms、qml、qmw分别为进入加热器的蒸汽流量、上级疏水流量和给水流量，kg／s；cp为给水平均比定压热容，kJ／（kg·℃）；Cq为散热损失系数，一般可取1.01～1.02。

2）对凝结段和疏水冷却段分别进行传热设计计算，其中凝结段对数平均温差Δtmc（℃）［6］为：

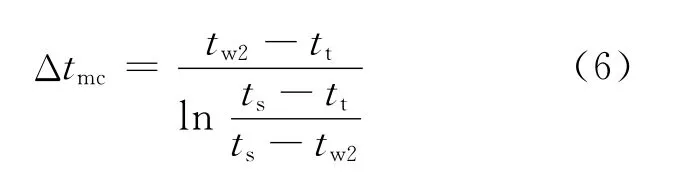
式中：tw2为给水出口温度，℃；ts为进入加热器的蒸汽温度，℃。

3）疏水冷却段对数平均温差Δtmdc（℃）［6］为：

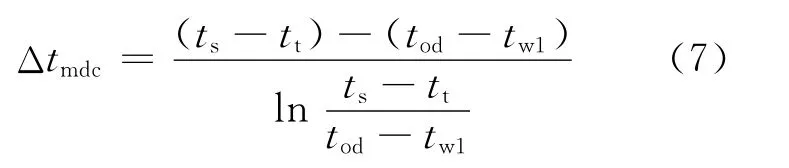
式中，tod为疏水出口温度，℃。

4）在凝结段，进入加热器的蒸汽在水平管束外凝结放热，当管外雷诺数Reoc＜2 100时，凝结段管外换热系数αoc（W／（m2·℃））［7］为：

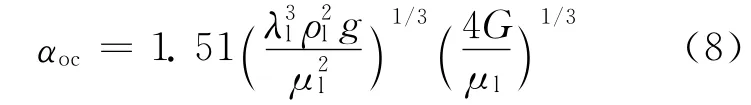
式中：λl为冷凝液导热系数，W／（m·℃）；ρl 为冷凝液密度，kg／m3；μl 为冷凝液黏度，Pa·s；g 为重力加速度，m／s2；G 为冷凝负荷，kg／（m·s）。

当Reoc＞2 100 时，凝结段管外换热系数αoc（W／（m2·℃））［7］为：

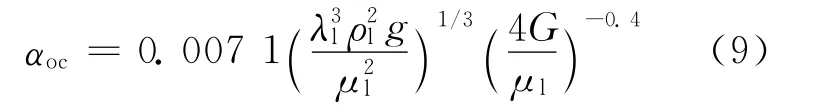
3.2 优化约束条件

基于工程限制及设备稳态性能要求，给定高压加热器优化约束条件。约束条件包括优化变量范围约束、给水出口温度约束、管程、壳程压降约束及管内流速约束，约束条件限制列于表1。

约束条件具体限制如下：1）将优化变量限制在所给定的变化区间内，其中优化变量选取高压加热器的主要结构参数，包括传热管外径、传热管总根数、传热管中心距及折流板间距；2）为满足高压加热器的加热性能要求，应保证给水出口温度至少达到母型值；3）高压加热器优化设计应保证管程、壳程压降低于母型的，从而降低压力损失；4）为防止不锈钢管侵蚀并尽量降低泵功耗，通常限制管内流速小于4.6m／s。

3.3 评价及优化结果

评价模型的计算值与母型值的对比结果，以及基于TCA、CCA 对高压加热器重量的优化设计结果列于表2。

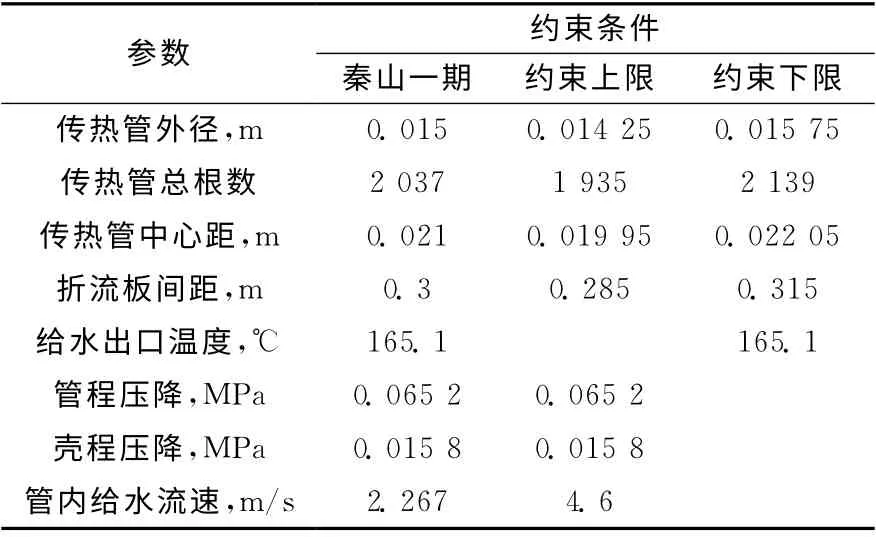
表1 约束条件Table 1 Limitation condition

表2 高压加热器重量的评价及优化结果Table 2 Assessment and optimized results of weight for high-pressure heater

由于高压加热器热工水力设计计算是基于简单计算模型的，同时各组成部分的重量采用了近似计算，因此计算结果存在误差。评价结果显示各参数的计算相对误差控制在5%以内，可认为基于所建立的数学模型的优化结果可信。

基于CCA，高压加热器的优化重量与评价模型计算结果相比减小了7.116%，优化效果显著。其中，优化变量与母型相比，传热管外径增大1.6%，传热管总根数减少0.982%，传热管中心距减少5%，折流板间距增大5%。高压加热器性能参数与评价模型计算结果相比，给水出口温度与评价模型计算结果一致，总换热面积减少1.667%，管侧压降减少8.558%，壳侧压降减少4.601%。优化结果证明，在满足高压加热器加热性能要求、压降约束、管道腐蚀及泵功耗约束的前提下，高压加热器重量有较大的优化空间。优化结果说明列于表3。

表3 优化结果说明Table 3 Explanation of optimized results

然而，基于TCA 的优化重量仅减小了6.194%，低于CCA 的优化率将近1%。CCA的优化性能明显高于TCA，虽然CCA 计算耗时高于TCA，但基于CCA 的高压加热器单次优化耗时近似为2 min，是可接受的。优化结果对比分析是以本文所建立的数学模型的计算结果作为参考，优化后重量的减小量并不包含数学模型评价结果的误差。本文将自主改进的CCA 应用于核电高压加热器重量的优化设计中，表明高压加热器结构参数的优化组合可实现其重量的减小，从理论上证明了高压加热器重量优化的可能性，可为核动力装置的设计提供理论优化方向。

4 结论

本文基于相似度最低建立多复合形的最优化组合，得到改进后的CCA。典型测试函数的优化结果证明，CCA 较TCA 具有更佳的全局搜索能力。基于CCA 实现了高压加热器重量的优化设计，得出以下结论。

1）群体初始复合形对可行域空间的覆盖面明显大于TCA，增强了算法对可行域空间状况的了解能力，群体复合形中任选1个复合形与其余复合形之间形成相似度最低的最优化组合，使被选复合形充分获取了其余各复合形的相对最优信息，算法的全局搜索能力显著提高。

2）典型函数Schwefel函数的优化结果证明，CCA 较TCA 具有更佳的全局搜索能力、计算精度及稳定性，虽然计算时间略大于TCA，但其实际偏差并不明显，计算时间的增加量对优化工作无太大影响。

3）将CCA 应用于核电高压加热器重量的优化设计计算，优化后，高压加热器的重量与评价模型计算结果相比减小了7.116%，优化效果明显，但优化过程未能全面考虑工程中的实际影响因素，优化结果可为工程设计提供理论参考。

［1］ 杨孟嘉，任俊生，周志伟.第4代核能系统研发介绍［J］.国际电力，2004，8（5）：30-35.YANG Mengjia，REN Junsheng，ZHOU Zhiwei.Introduction of R＆D on generationⅣnuclear energy system［J］.International Electric Power for China，2004，8（5）：30-35（in Chinese）.

［2］ SACCO W F，FILHO H A，HENDERSON N，et al.A metropolis algorithm combined with Nelder-Mead simplex applied to nuclear reactor core design［J］.Annals of Nuclear Energy，2008，35（5）：861-867.

［3］ VIVAS G F C，PARISH T A，CURRY G L.Optimization of MOX enrichment distributions in typical LWR assemblies using a simplex methodbased algorithm［J］.Annals of Nuclear Energy，2002，29（17）：2 001-2 017.

［4］ 李亮，迟世春，林皋.改进复合形法及其在边坡稳定分析中的应用［J］.哈尔滨工业大学学报，2005，37（10）：1 429-1 432.LI Liang，CHI Shichun，LIN Gao.Modified complex method and its application to the slope stability analysis［J］.Journal of Harbin Institute of Technology，2005，37（10）：1 429-1 432（in Chinese）.

［5］ 贺士晶，阎昌琪，王建军，等.复合形-遗传算法在核动力设备优化设计中的应用研究［J］.核动力工程，2010，31（2）：122-125，135.HE Shijing，YAN Changqi，WANG Jianjun，et al.Research on application of complex-genetic algorithm in nuclear component optimal design［J］.Nuclear Power Engineering，2010，31（2）：122-125，135（in Chinese）.

［6］ 能源部西安热工研究所.热工技术手册（第三篇）：汽轮机组［M］.北京：水利电力出版社，1991：295-303.

［7］ 钱颂文.换热器设计手册［M］.北京：化学工业出版社，2002：55-92.

［8］ 顾琼彦，虞佶，奚磊.高压加热器管板计算方法简析［J］.电站辅机，2011，32（3）：13-17.GU Qiongyan，YU Ji，XI Lei.Simple analysis on the calculation of the tube-sheet in high pressure feedwater heater［J］.Power Station Auxiliary Equipment，2011，32（3）：13-17（in Chinese）.