压水堆主泵飞轮周围间隙流中泰勒涡传热特性的数值研究

罗宇辰，刘应征，陈汉平

（上海交通大学 机械与动力工程学院 动力机械及工程教育部重点实验室，上海 200240）

第三代压水反应堆采用先进的非能动设计，可靠性要求严格。反应堆冷却剂主泵是核岛中唯一的高速转动部件，因此其可靠性要求更为严格。为满足需求，三代反应堆冷却剂主泵使用全密闭、高惯性的单级离心式屏蔽泵［1］。

屏蔽泵的转子两端安装有转动惯量很大的飞轮装置，以保证转子有足够的惰转时间。在失去电源的状态下，反应堆冷却剂泵仍能提供足够的惰转流量，充分冷却堆芯。飞轮不仅为主泵转子提供惯性，还是主泵重要的传热通道。飞轮上方是主泵出口的高温流体腔室。飞轮下方是主泵长轴，长轴周围布置电机线圈和冷却系统，以保持线圈正常的工作温度。飞轮连同其周围的静止构件承担着将飞轮上腔壁面热量引导到下方冷却系统的功能，飞轮和周围构件自身的温度分布也受热流分配的影响。高速旋转的飞轮与周围静止部件间设有间隙，间隙内充满流体。飞轮圆柱面和上下端面间隙的流体腔室联成一个整体。间隙流体与主泵长轴周围的冷却流体系统只有极小的缝隙相通，基本上相互隔绝。飞轮周围间隙中的流体虽然处于封闭状态，但内部流动十分复杂，且对主泵传热起着重要作用。在飞轮与静止构件的壁面摩擦作用下，间隙流体作周向高速剪切流动并伴有强烈的二次流动。相对高速旋转的两个圆柱间产生的二次流就是泰勒涡。不同的旋转雷诺数下泰勒涡呈现不同的形态。泰勒涡的存在大幅改变了间隙流体的传热特性，增强了飞轮上方主泵热壁面向下部长轴冷却系统传递热量的能力，同时改变了飞轮和周围承力部件的温度分布。本文研究飞轮间隙中湍流泰勒涡的传热特性，为主泵飞轮及周围承力部件的温度场计算和强度考核提供基础。

1 泰勒涡特征概述

当流体处于两个以不同速度旋转的同心圆柱之间时，圆柱壁面上的流体随壁面作无滑移运动，圆柱间隙中的流体作简单的环状剪切运动。由于离心力的存在，外壁处的流体压力大于内壁，流体压力差与离心力相平衡。当内外圆柱转速差较大且间隙尺度远小于其半径时，离心力与压力差平衡下的简单环状流被破坏，内环表面某些位置上的流体在离心力作用下越过间隙直接流向外环。此时流体除作环状流动外，在间隙的法向截面中还将形成若干组成对反向旋转的漩涡，该流动状态用Taylor［2］的名字来命名，称为泰勒涡。泰勒涡的形态变化非常复杂，它与流体物性、流域几何和运动边界都有关系，可用一个准则数“泰勒数”Ta 来描述，特定的泰勒数对应着一个确定的泰勒涡流态。泰勒数以及相应雷诺数可定义为：

式中：ω 为内圆柱面转速；R1为内圆柱面半径；R2为外圆柱面半径；ν为流体运动黏度；Re为雷诺数；d为间隙宽度；U 为内圆柱旋转线速度。

Anderreck等［3］为内外圆柱施加不同的旋转方向及旋转速度，通过实验测定了18种流动状态。观察发现：当外圆柱固定时，随内圆柱转速提高依次出现库塔流动、层流泰勒涡、波动流以及湍流泰勒涡等不同的流动现象。库塔流动是一种简单的剪切流动，该流动只有切向速度，在轴向和径向无速度分量。流动呈平稳的层流状态，流线呈现以转轴为中心的环状走向。转速逐渐增大，泰勒数提高到某一数值时，出现层流泰勒涡，把该泰勒数定义为临界泰勒数Tac。Tac的大小与几何结构有关。层流泰勒涡是一种具有较强反向旋转环形二次流的流动状动。层流泰勒涡环面轴线与内圆柱旋转轴平行。当内圆柱的旋转速度进一步增大时，层流泰勒涡呈现切向不均匀性，涡环轴线不再与内圆柱轴线平行，间隙流进入了波动流状态。持续提高内圆柱转速，波动流减弱，圆环形二次流动也逐渐消失，流动进入湍流状态。内圆柱转速继续上升，湍流流动开始出现，其形式与层流泰勒-库塔流动类似，对应的雷诺数及其流动特征都已进入湍流范围。额定工况下核电主泵飞轮间隙内冷却流的泰勒数就落在生成湍流泰勒涡的范围之内。

19世纪末以来，有关间隙内部湍流泰勒涡机理的实验和数值研究有过大量文献报道。最早在文章中提到湍流泰勒涡的是Pai［4］，但他没有对泰勒涡进行系统的定量研究。首先系统地研究湍流泰勒涡的Coles［5］在1965年的文章中展示了一组湍流泰勒涡的照片。Fenstermacher等［6］和Walden 等［7］在 相 当 大 的 泰 勒 数 范 围内，通过实验测定了旋转圆柱间隙中流体的流动特性。他们发现在泰勒数非常高时，环状对称的流动结构仍存在。Koschmieder［8］详细讨论了随着泰勒数增大，流动轴向波长（即泰勒涡对数目）的变化。

2 数学模型

湍流泰勒涡的控制方程与一般黏性流动的控制方程一样，包括质量方程、动量方程（N-S）和能量方程：

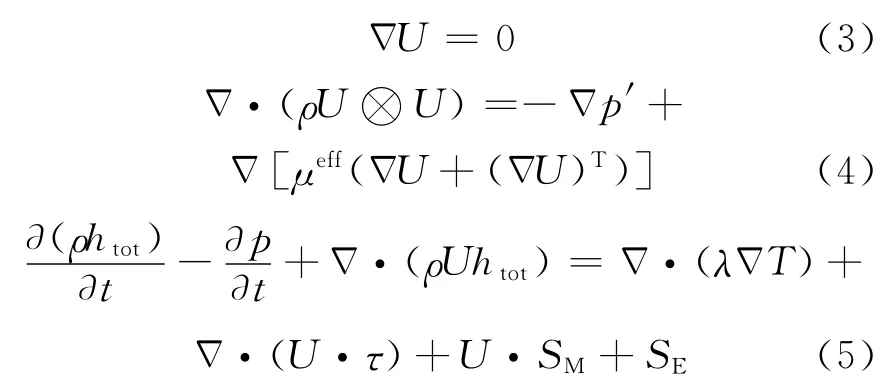
式中：htot=h+U2为总焓·（U·τ）代表黏性力做功；U·SM表示外部动量源的功；SE为位能。

为获取湍流的时均速度场，需将上述控制方程作时均化处理消除方程的瞬态项，再引入湍流模型使方程封闭求解。合适的湍流模型对模拟泰勒涡有重要影响。核电主泵飞轮冷却流中的湍流泰勒涡具有强湍流输运性、体积力和强烈不平衡效应，此时基于各向同性假设涡黏模型失效，如k-ε 模型。而雷诺应力模型（Reynolds stress model，RSM）能准确地描述流线弯曲、应力突变、二次流、离心力、浮升力等复杂因素，因此采用雷诺应力模型更为合理。

本文以Koschmieder［8］提供的旋转圆柱窄间隙流的实验模型和参数为验证计算的对象。实验模型间隙比η=R1／R2=0.896，高度间隙比为123.5。分别用雷诺应力模型、标准k-ε 模型和 剪 切 应 力 输 运（shear stress transport，SST）模型模拟。计算采用实验工况，内圆柱快速启动转速升至泰勒数7 633 006，即3 800Tac。其中，快速启动指内圆柱加速至最终转速所用的时间，远小于流体从不稳定状态恢复到稳定平衡状态所用的时间。计算中直接给内圆柱施加最终的旋转速度，不考虑加速的过程。结果表明，不同湍流模型模拟得到的泰勒涡对数有所不同。使用雷诺应力模型计算出间隙中存在51对泰勒涡，与实验相符，标准k-ε 模型和剪切应力输运模型的模拟结果与实验相差较大。因此，本文在核电主泵飞轮冷却流泰勒涡流动传热特性数值研究中选定RSM 为湍流模型。

表1 不同湍流模型对湍流泰勒涡的模拟结果Table 1 Results of turbulent Taylor vortices simulation using different turbulent models

3 飞轮周围间隙流中泰勒涡流动与传热特性的数值研究

3.1 物理模型和计算区域提取

本文的物理模型的选取依据核电主泵结构，提取发生在主泵飞轮周围间隙内的流动与传热行为。物理模型包括主泵的旋转轴、飞轮、周围静止承力与传热构件，以及飞轮与周围静止构件间隙内的流体。间隙与外部冷却系统的出入口很小，流体质量交换被忽略。物理模型呈轴对称状态，计算中可取半个剖面分析。飞轮上部主泵热壁面通过该物理模型实施热流分配，从而决定部件的温度分布。物理模型中固体部分的传热特性简单，易于计算。飞轮周围流体的流动状态和传热特性非常复杂，对主泵热流分配和构件温度场有重要影响。因此该物理模型的研究重点就是飞轮周围间隙内流体的流动和传热特性，数值计算的区域选定为飞轮周围间隙中的流体区域。

飞轮周围间隙流的计算区域示于图1。内部边界是主泵轴、飞轮圆柱表面和上下端部表面，外部边界是飞轮周围的静止构件表面。计算区域分成3个部分：飞轮圆柱面外部的长环形流柱和飞轮上、下端面外部的扁环形流柱。计算域采用圆柱坐标系（r，θ，z），对应的流体速度分量分别为（径向速度Vr，切向速度Vθ，轴向速度Vz）。以飞轮侧面的外法线方向为r正方向。

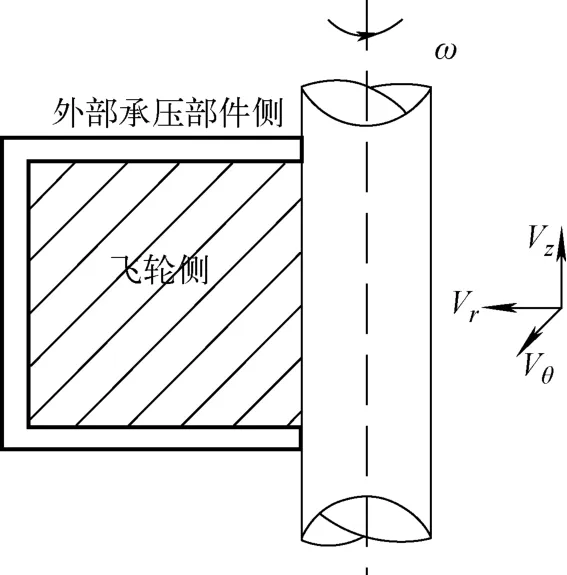
图1 计算模型Fig.1 Computational model

边界条件设置：间隙流体的流动边界均取无滑移边界条件；飞轮圆柱面、上下端面和主轴表面均取主泵额定转速下的圆周速度；周围静止件处的边界速度均取为零。

计算域采用全六面体结构网格，几何模型经PRO／E 软件建模后，由ICEMCFD 进行网格划分。经网格无关性分析，采用全域网格数为1 711 564、网格节点为1 582 050 的网格。泰勒涡控制方程采用雷诺应力湍流模型使时均方程组封闭，数值模拟采用有限控制体积法，应用CFX 计算软件。

3.2 飞轮周围间隙流的流场结构研究

飞轮周围间隙流没有进出口，流体处在封闭的间隙腔内由飞轮带动作高速旋转运动。间隙内的主流保持轴对称周向运动状态。由于间隙两侧的固体边界速度差很大，间隙宽度较小，致使间隙流存在巨大的法向速度梯度。

飞轮圆柱侧面间隙的长环形柱体结构完全符合发生泰勒涡的几何特征。不同的流动参数条件下，间隙中将出现不同的泰勒涡对，并可用轴向波长参数来描述泰勒涡对的结构。本文在核电主泵额定转速下计算了飞轮间隙流的全域速度矢量分布。计算结果表明，飞轮圆柱面间隙中轴向分布有6对泰勒涡，中间几对形态相似，靠近上下端面的两个涡对由于受端壁边界的约束出现一定程度的畸变。泰勒涡的图谱如图2所示。本文计算结果与Burkhalter等［9］的研究结论相一致。

图2 泰勒涡的形态与分布Fig.2 Shape and distribution of turbulent Taylor vortices

旋转流场下，长环形柱体内出现泰勒涡对流动图谱，本质上是离心力、流体压力和黏性力平衡的结果。当内壁转速较低或间隙宽度较大时，间隙流动处于简单的剪切旋转流状态，内壁向外壁的离心力与外壁向内壁的流体压力相平衡，流场内无二次流发生。不过离心力与流体压力这种平衡并不是一成不变的，可能有多种平衡模式。当内壁旋转速度较高而间隙较小时，内壁某处的流体在离心力作用下冲向外壁，在黏性力的帮助下形成涡对。不同的旋转泰勒数对应不同的涡对图谱，并在剪切旋转主流场中出现不同的二次流动。尽管泰勒涡流场中二次流的速度较周向主流速度小得多，但它参与间隙的法向传热，因此对飞轮间隙流的传热特性有重要影响。周向主流速度虽很大，而因间隙内流体温度场呈轴对称分布，周向主流对传热并未做出贡献。本文从图2中截取飞轮圆柱面间隙中的1对泰勒涡的流场图谱，经放大勾画出泰勒涡参与热量输运的路线，如图3所示。图中热壁附近C 处的流体在泰勒涡裹挟下直接流向冷壁D，并在冷壁附近形成高温带DA。同样，在热壁附近形成低温带BC。这意味着泰勒涡将冷热壁的距离大幅拉近，从而强化了传热。

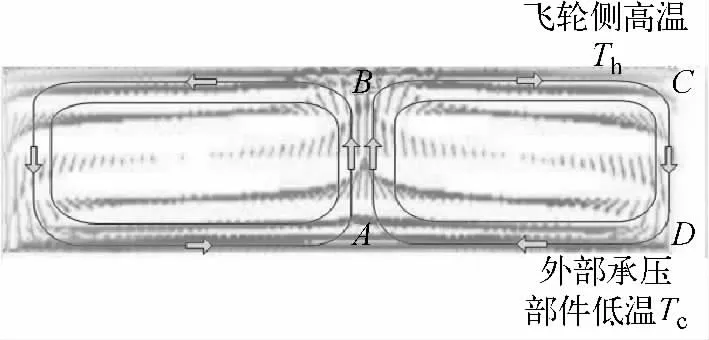
图3 泰勒涡参数热量输运的路线Fig.3 Distribution of Taylor vortices in gap of two concentric cylinders（side）

飞轮上、下端面间隙中同样存在离心力、流体压力与黏性力的平衡问题。但端面内、外径处的尺度和周向速度差别很大，不可能像飞轮圆柱面间隙那样产生对称、有序的泰勒涡对，而是形成一个覆盖整个飞轮端面的大尺度扁环形涡胞，如图2所示。涡胞造成的二次流同样有垂直于飞轮端面的法向速度，从而增强了端面间隙流的传热能力。

3.3 飞轮周围间隙流传热特性研究

飞轮高速旋转对周围构件温度场产生两项重要影响：其一，飞轮高速旋转产生的间隙内流体的强烈二次流改变了飞轮间隙及周围的传热特性；其二，包括二次流在内的飞轮间隙高速剪切湍流摩擦内热源提高了飞轮周围构件的温度。本文主要研究第1项飞轮间隙流存在泰勒涡情况下传热特性的变化。对于第2项内热源问题，则在主泵固体构件温度场计算中由附加剪切湍流摩擦功或直接采用流固耦合的算法加以解决。

飞轮间隙中的传热主要发生在飞轮的法线方向，且由泰勒涡来完成。周向运动的主流不参与热传导。飞轮间隙流的法向传热量取决于法向壁面温差和壁面换热系数。壁面换热系数则由流场和泰勒涡的结构所决定，并不依赖于温度分布。因此飞轮间隙流的传热量计算可在假设飞轮和静止壁面分别处于定壁温的条件下求解间隙流能量方程（5）得到。本文取静止壁面温度为高温Th，飞轮壁面温度为低温Tc，壁面温差ΔT。流体物性按壁面平均温度取定。求解能量方程得到间隙流体的全场温度分布，包括近壁网格点的温度Tw。

图4为计算得到的飞轮圆柱面近壁网格点无量纲温度T＊w沿圆柱高度的变化，无量纲温度定义为T＊w=（Tw-Tc）／（Th-Tc）。由图4可见，近壁温度沿圆柱高度呈明显的周期性变化，周期数与泰勒涡对数完全一致。1个周期内近壁网格点温度的变化幅度并不很大，仅为间隙两侧壁面温差的10%左右。全周期内近壁无量纲平均温度为0.66，这表明离壁1个网格的距离内承受了间隙总温差的34%。显然，泰勒涡提高了近壁局部区域的温度梯度，增强了流体传热。

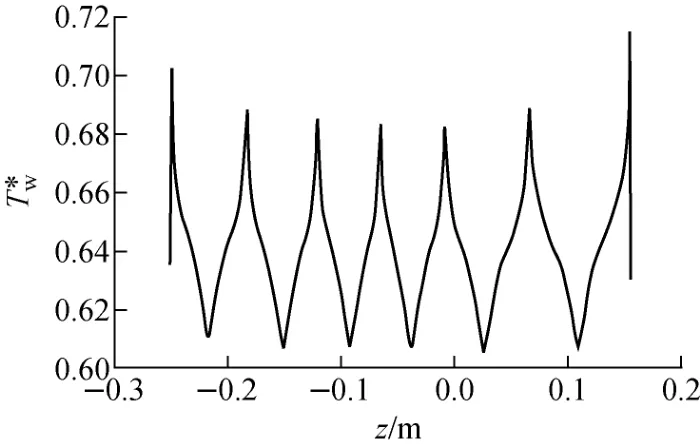
图4 间隙流飞轮侧圆柱面温度随高度的变化规律Fig.4 Distribution of temperature on side of flywheel

根据湍流壁面函数法，可利用近壁温度按式（6）计算当地边界热流：

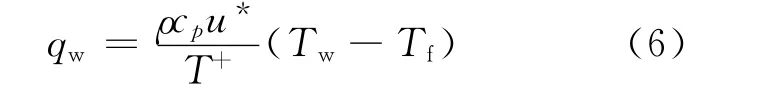
式中：qw为壁面热流密度；Tw为壁面温度；Tf为靠近壁面流体温度。边界层无量纲近壁面距离y+处有无量纲温度T+和剪切速度u＊，u＊是湍动能k的函数。u＊、T+和y+等湍流壁面函数的计算由软件CFX 完成。应用壁面函数法对计算域网格划分有要求，近壁第1网格点必须落在湍流边界层对数率区段之内，本文计算中y+在20～30之间，满足要求。

图5为壁面热流密度qw沿壁分布的计算结果。与近壁温度分布一样，边界热流同样呈现泰勒涡的周期特征。为便于比较，将间隙中的法向速度同时展示在图5中。图5清晰表明两者不仅周期相同，且高度相关，而相位上则相差半个周期。两者相关性表明边界热流和法向速度是同一泰勒涡在传热和流动两个方面的反映。法向速度为负方向最大值时，外壁冷流体冲向热壁，内壁出现最大热流密度。同理，法向速度为正方向最大值时，内壁热流体离开热壁，内壁面附近温度梯度减小，内壁产生最小热流密度。图5显示的壁面热流包括泰勒涡二次流与流体热传导两者的共同贡献。计算表明，在飞轮间隙流的条件下泰勒涡的贡献较流体导热大1个数量级。

图5 间隙流飞轮侧圆柱面热流密度和法向速度随高度的变化规律Fig.5 Distribution of heat flux and normal velocity on side of flywheel

飞轮端面热流密度及间隙内法向速度示于图6。端面间隙中的流动机理与圆柱面间隙相似，也是由离心力、流体压力和黏性力的共同作用形成漩涡。由于几何条件的差异，端面间隙中只出现1个扁环涡，而没有周期性的泰勒涡对。扁环涡同样参与并增强传热，壁面热流与法向速度的对应关系也与圆柱面间隙中相类似。

图6 间隙流飞轮侧上端面热流密度和法向速度随径向的变化规律Fig.6 Distribution of heat flux and normal velocity on top of flywheel

由于边界当地热流是依赖于壁面温度的有因次量，对泰勒涡传热特性研究结果的应用造成一定局限。采用壁面努塞尔数则可消除壁温差异带来的影响，从而增加泰勒涡传热特性模拟结果的普遍性。根据努塞尔数Nu的定义：

其中：换热系数h 利用qw计算得到，h=qw／ΔT，ΔT 为给定的间隙两侧边界温差；特征尺度L 取飞轮间隙的法向宽度；λ 为间隙中冷却流体的导热系数。由此得到壁面边界的当地努塞尔数为：

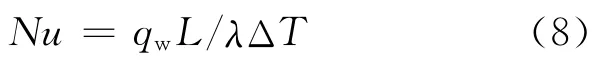
式中，L、λ和ΔT 均为常数，故边界努塞尔数曲线的走势与边界热流完全一致。对应本文泰勒涡的最大和最小边界努塞尔数分别为1.36×103和4.55×102。

本文中的Nu是在额定工况下得到的数据。在该工况下，间隙流体雷诺数Re为7.38×106，普朗特数Pr为0.967，几何参数长度与间隙的比值L／d为32。对于核电主泵处于变工况运行的情况，当自变量确定后可采用与上述设计工况同样的CFD方法直接计算泰勒涡Nu。

4 结论

通过数值模拟的方法，得到了湍流泰勒涡的流动和传热特性。飞轮间隙流中的传热特性受湍流泰勒涡影响出现了周期性变化的特征。

由于湍流泰勒涡的存在，核电主泵飞轮冷却流的传热得到强化；使用雷诺应力模型，能很好地模拟湍流泰勒涡，模拟结果与实验结果吻合良好；流动特性和传热特性是泰勒涡特性在两个方面的显示，两者具有高度相关性。

［1］ 马习朋.第三代核电AP000主冷却泵的变频设计方案探讨［J］.电力设备，2007，8（12）：20-23.MA Xipeng.Discussion on design scheme of frequncy-conversion for AP1000’s main-coolant pumps［J］.Electrical Equipment，2007，8（12）：20-23（in Chinese）.

［2］ TAYLOR G I.Stability of a viscous liquid contained between two rotating cylinders［J］.Pilosophical Transactions of the Royal Society London A，1923，223：289-343.

［3］ ANDERRECK C D，LIU S S，SWINNEY H L.Flow regimes in a circular Couette system with independently rotating cylinders［J］.Fluid Mech，1986，164：155-183.

［4］ PAI S.Turbulent flow between rotating cylinders［R］.［S.l.］：NACA，1943.

［5］ COLES D.Transition in circular Couette flow［J］.J Fluid Mech，1965，21：385-425.

［6］ FENSTERMACHER P R，SWINNEY H L，COLLUBC J P.Dynamics instability and the transition to chaotic Taylor vortex flow［J］.J Flow Mech，1979，94：128-133.

［7］ WALDEN R W.Reemergent order of chaotic circular Couette flow［J］.Phys Rev Lett，1979，42：301-304.

［8］ KOSCHMIEDER E L.Turbulent Taylor vortex flow［J］.J Fluid Mech，1973，93：515-537.

［9］ BURKHALTER J E，KOSCHMIEDER E L.Steady supercritical Taylor vortex flow［J］.J Fluid Mech，1973，58（3）：547-560.