耗散系统中原子和场的熵交换与纠缠
岳转林,闫学群
(天津工业大学理学院,天津300387)
1 引 言
量子关联研究中,发现熵交换可以说明量子系统由纯态变为混合态时损失的有效信息. Jaynes-Cummings (J-C)模型是一种描述原子与场相互作用的理想量子动力学模型[1-3]. 因而,该模型中原子与场相关联的熵演化现象已经成为量子信息学的研究热点[4-7]. Phoenix 和Knight 研究了纯态下原子与场相关联的熵演化现象,并证明了原子与场两子系统的约化熵在演化过程中始终相等[8]. 之后,很多科学家对原子与场处于混合态的该现象进行了深入研究. Boukobza 和Tannor 发现了原子与场的初态均处于混合态时,它们的约化熵不一定相等,并在一定条件下发生熵交换,两者之间出现反相关联的现象[9]. 此外,纠缠是量子信息处理中不可或缺的物理资源[10-13]. 我们已经知道纯态双子系统的纠缠可以用约化熵度量,Boukoba 等也研究了混合系统中熵交换和纠缠[9].文献[14]研究了单模场中,原子与场的熵交换与纠缠在演化过程中呈相反的变化趋势. 近年来,两子系统的熵交换与纠缠的关系被广泛研究[16-17]. 然而这些研究忽略了场腔与外界环境相互作用对两子系统熵交换和纠缠的影响. 在实际情况中,原子与场相互作用系统的熵交换和纠缠在演化过程中总会受到场的能量损耗的影响. 因此,研究耗散腔中的原子与场的熵交换与纠缠更有实际意义.
本文考虑了场腔耗散的影响,利用解线性微分方程组的方法,对共振情况下的二能级原子和耗散场相互作用体系的刘维方程进行精确求解.计算了原子与场的约化熵和两子系统间的纠缠度,并利用结果讨论了原子与耗散场的熵交换条件,还发现原子与场发生熵交换时,两者之间的纠缠为零.
2 系统模型与密度矩阵
两能级原子置于单模场中,在偶极作用和旋波近似下的系统哈密顿量为(这里令ħ =1)[17]:
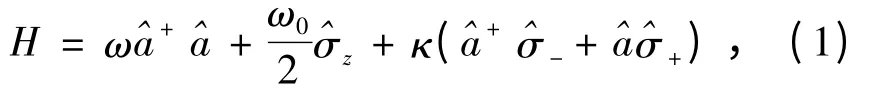
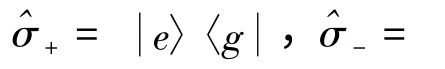
这里假设场的初态为单模热态:
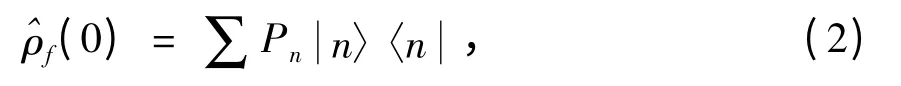
其中Pn= [mn/ (m + 1)n+1],这里m 代表腔中的平均光子数.
设原子的初始态为混合态:
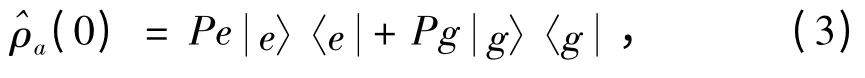
其中0 ≤Pe ≤1 ,且Pg = 1 -Pe 是原子混合态的参数,Pe = 0 代表原子处于基态,Pe = 1 代表原子处于激发态.
那么系统的初始态可以定义为:
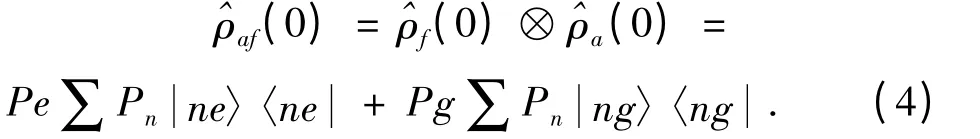
在我们讨论的问题中,考虑下列含有耗散项的演化方程:
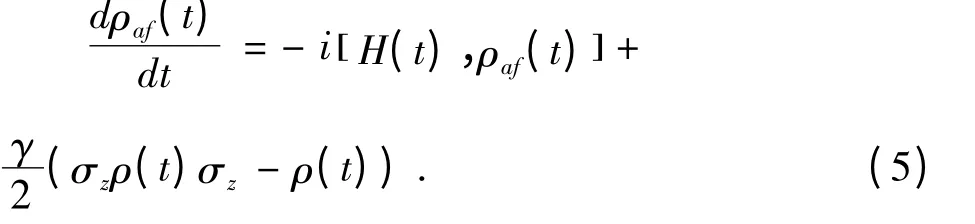
其中,γ 是耗散系数. 将方程(1),(4)代入方程(5)中,可以计算得到系统的密度算符的表达式,(为简单起见而又不失一般性,令ω - ω0= 0)
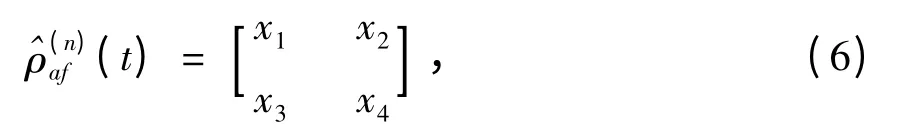
这里,
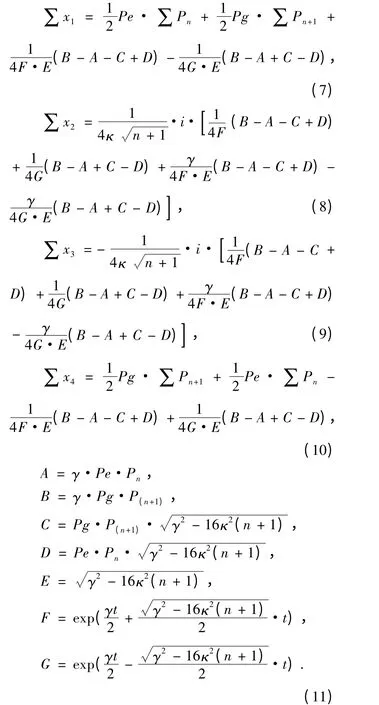
3 原子与场的熵交换与纠缠
量子系统的熵定义为:

其中^ρ 是给定量子系统的密度算符. 这里我们令玻尔兹曼常数为1,密度算符^ρ 可以写成矩阵形式,容易计算出它的本征谱为{λi}. 因此熵可以写成:

为了研究原子与场之间的熵关联,必须计算出原子和场的约化熵. 以下我们标记两个子系统为a 和f,两个子系统总的密度算符为^ρ,子系统的密度算符为^ρa和^ρf,子系统的密度算符由下式
给出:
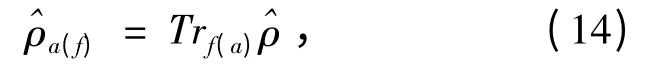
因此两个子系统的熵分别为:
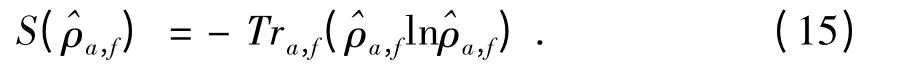
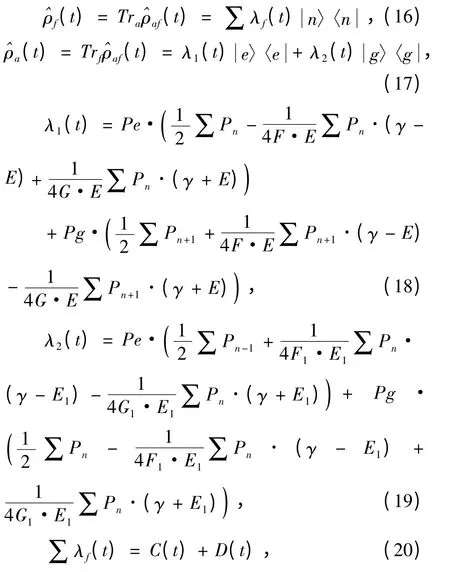
这里,
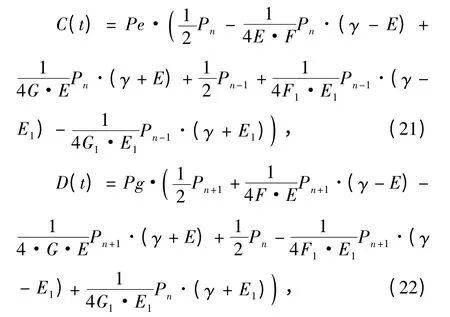
其中,

由(13)式得到场与原子的熵:
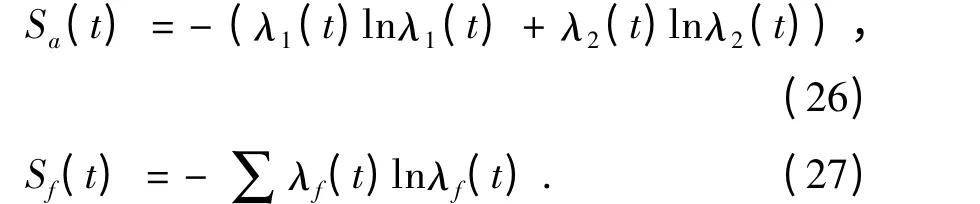
由(26),(27)式可得到原子与场的熵的数值结果:
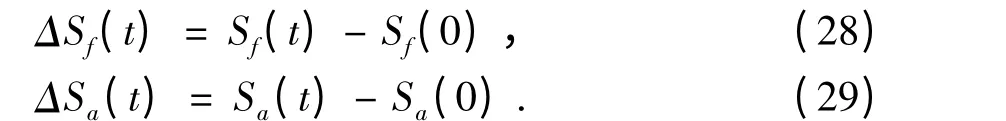
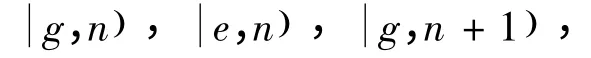
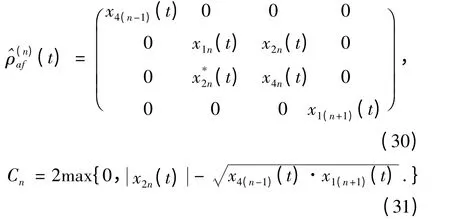
4 数值分析
通过上面的理论计算,我们分析现有模型中原子和场的熵变换的数值结果. 进而证明了在一定条件下,原子与场的熵交换是反相关联的.
图1(a)中描述的是当场的初始态是弱激发热态m = 0.2 ,原子的初始态是混合态Pe = 0.8时,原子与场的熵变化ΔS(t)随时间γt 的变化趋势. 其中,实线代表的是场的熵变化,虚线代表的是原子的熵变化. 从图中我们看到随时间γt 的增加,原子与场的熵变化趋势逐渐不同,这与孤立系统中的变化趋势(原子与场的熵变化是同时上升或者是同时下降)有所不同. 导致这种现象的原因是耗散场要向外界不断的辐射光子,熵增加的更快一些,致使场的熵增加得快一些. 这与热力学中的熵增加原理完全相符合. 图1(b)中Pe= 0.1 ,m = 0.2 ,我们可以清楚的看到原子与场的熵变化呈现相反的变化趋势,ΔSa+ ΔSf也呈振荡变化. 当Pe 和m 取合适的值时,ΔSa+ΔSf的图像是一条光滑的曲线,变化方向与场约化熵的变化方向相同.
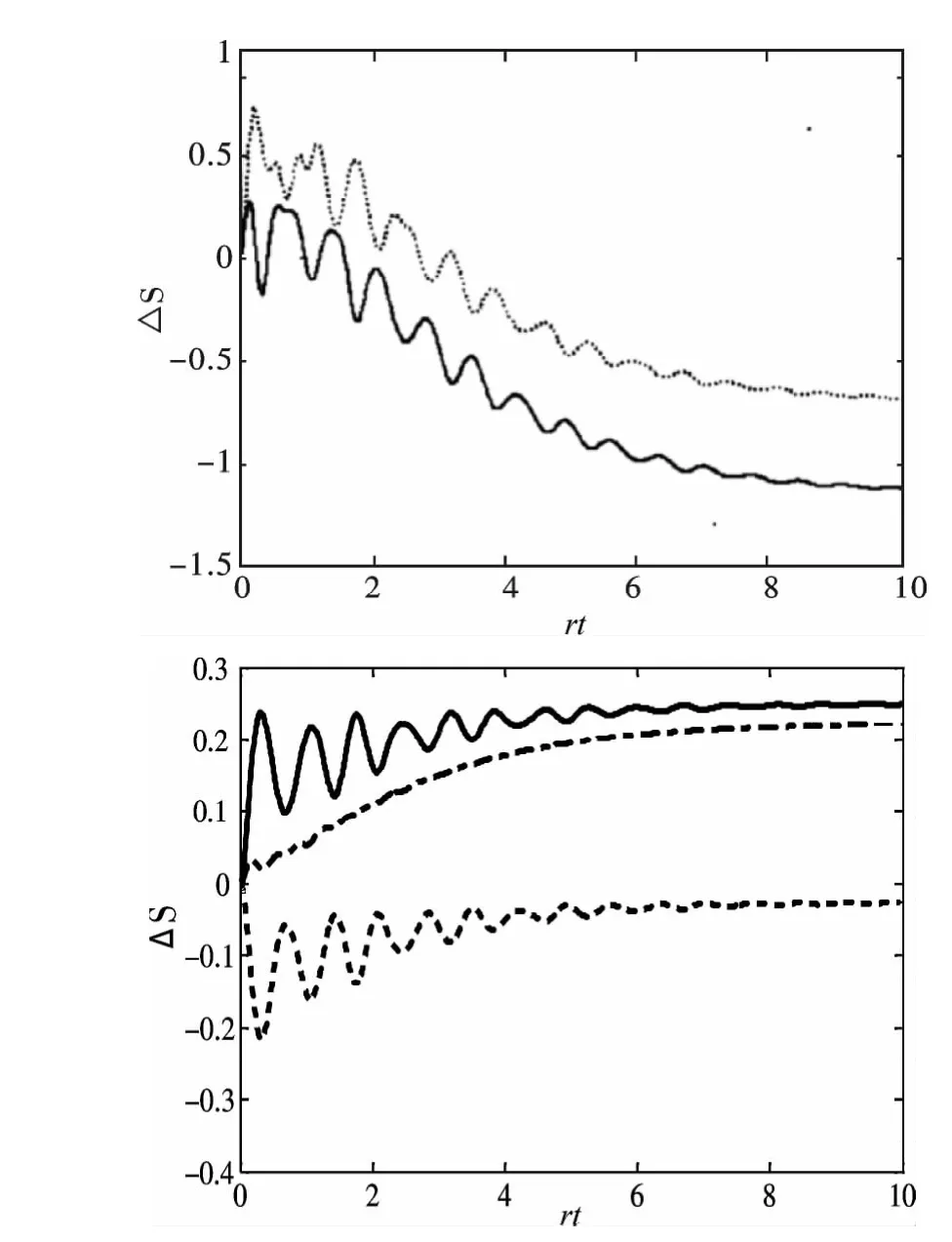
图1 当κ/γ = 20 时部分熵ΔS 随时间变化趋势. (a)场的初始态是热激发场m =0.2 ,原子的初始态是接近于激发态Pe=0.8.(图中实线代表场的熵变化,虚线代表原子的熵变化). (b)场的初始态是热激发场m = 0.2 ,原子的初始态是混合态Pe =0.1,(实线代表场的熵变化,虚线代表原子的熵变化,点画线代表的是场与原子熵变化的和)Fig.1 Plots of the change of partial entropy with time ΔS(t)for=20. (a)The field is initially in a weakly excited thermal field m = 0.2 and the atom in the mixed state Pe = 0.8(field:solid line,atom:dotted line);(b)The field is initially in a weakly excited thermal field m = 0.2 and the atom in the mixed state Pe = 0.1(field:solid line,atom:dotted line,atom plus field:dash-dot line)
图2 曲线上对应的Pe 和m 的值,是原子与场的熵交换呈现反相关联的条件. 并且我们发现固定Pe 的值不变,减小m 的值,场的熵是负值,原子的熵是正值,即这些点落到A 区域ΔSf<0 ,ΔSa>0 ,增大m 的值,这些点落到B 区域ΔSf>0 ,ΔSa<0 . 图2 中的曲线与无耗散项的曲线上的点都代表原子与场的熵交换时对应的Pe 和m的值,但这些点代表的物理意义有所不同. 无耗散项的曲线上的点表示原子与场熵变化量之和是相等的,即Sa(t)- Sa(0)= -[Sf(t)- Sf(0)].而本文讨论的有耗散项曲线上的点代表的是原子的熵变化量小于场的熵变化量. 因为,本文的量子系统是开放系统,随着时间t 的变化,腔中有光子向外辐射,场熵的增加要比原子的熵增加快一些,Sa(t)- Sa(0)<-[Sf(t)- Sf(0)]. 这一点我们在下面将给出证明.
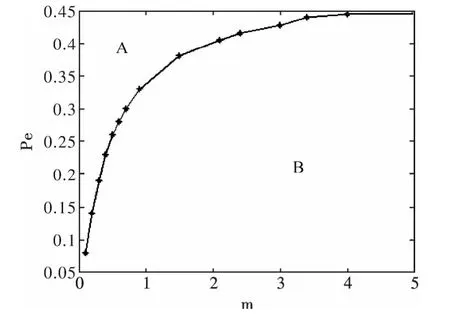
图2 图中的实线代表的是场的熵变化量大于原子的熵变化量:Sa(t)- Sa(0)<-(Sf(t)- Sf(0)),在A 区域,有ΔSf <0,ΔSa >0 ,在B 区域,有ΔSf >0 ,ΔSa<0Fig.2 The solid line represents the field entropy change being larger than that of atomSa(t)- Sa(0)<- (Sf(t)- Sf(0)).In region A,ΔSf <0 and ΔSa >0 ,in region B,ΔSf >0 and ΔSa <0
为不失一般性,我们选择一点Pe = 0.23 ,对应图2 中曲线上的m 值,m 的值是介于0.42 和0.43 之间. 图3 (a)中当m = 0.42 时,场熵变化是负值(ΔSf<0 ),原子的熵变化为正值(ΔSa>0 ). 图3 (c)中当m = 0.43 时,原子和场的发生了熵交换,场的熵变化是正值(ΔSf>0 ),原子的熵变化是负值(ΔSa<0 ). 同时可以发现当场的熵变化是正值时,ΔSa+ΔSf>0 ,当场的熵变化是负值时,ΔSa+ ΔSf<0 . 也就是说,当Pe和m 取不同的适当的值时,都会存在场熵变化量的绝对值总是大于原子熵变化量的绝对值. 故而可以证明场熵的增加要比原子的熵增加快一些,即Sa(t)- Sa(0)<-[Sf(t)- Sf(0)].
原子与场的熵变化的发生交换时,Pe = 0.23,m = 0.42 或m = 0.43 ,由图3 (b)和(d)可知,这时它们的纠缠是零.
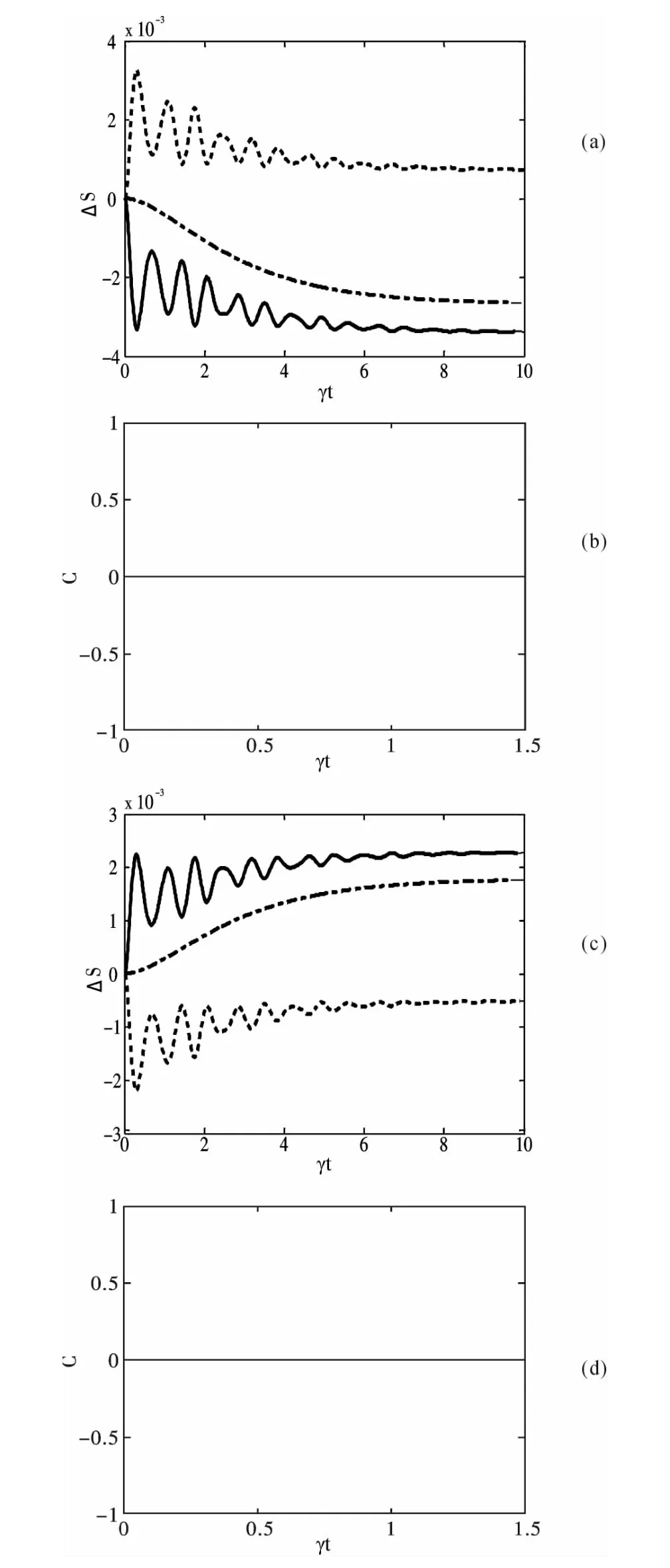
图3 (a)和(c)κ/γ = 20 时,原子与场的熵交换. (实线代表场的熵交换,虚线代表原子的熵交换,点画线代表原子与场的熵变换的和). (b)和(d)是原子与场的纠缠图. (a)和(b)Pe=0.23,m=0.42;(c)和(d)Pe=0.23,m=0.43Fig.3 (a)and (c)are partial entropy change (field:solid line,atom:dotted line,atom plus field:dash -dot line)for κ/γ = 20 . (b)and (d)are the concurrence between atom and field for κ/γ = 20 .(a)and(b)Pe = 0.23,m = 0.42 ;(c)and (d)Pe =0.23,m = 0.43
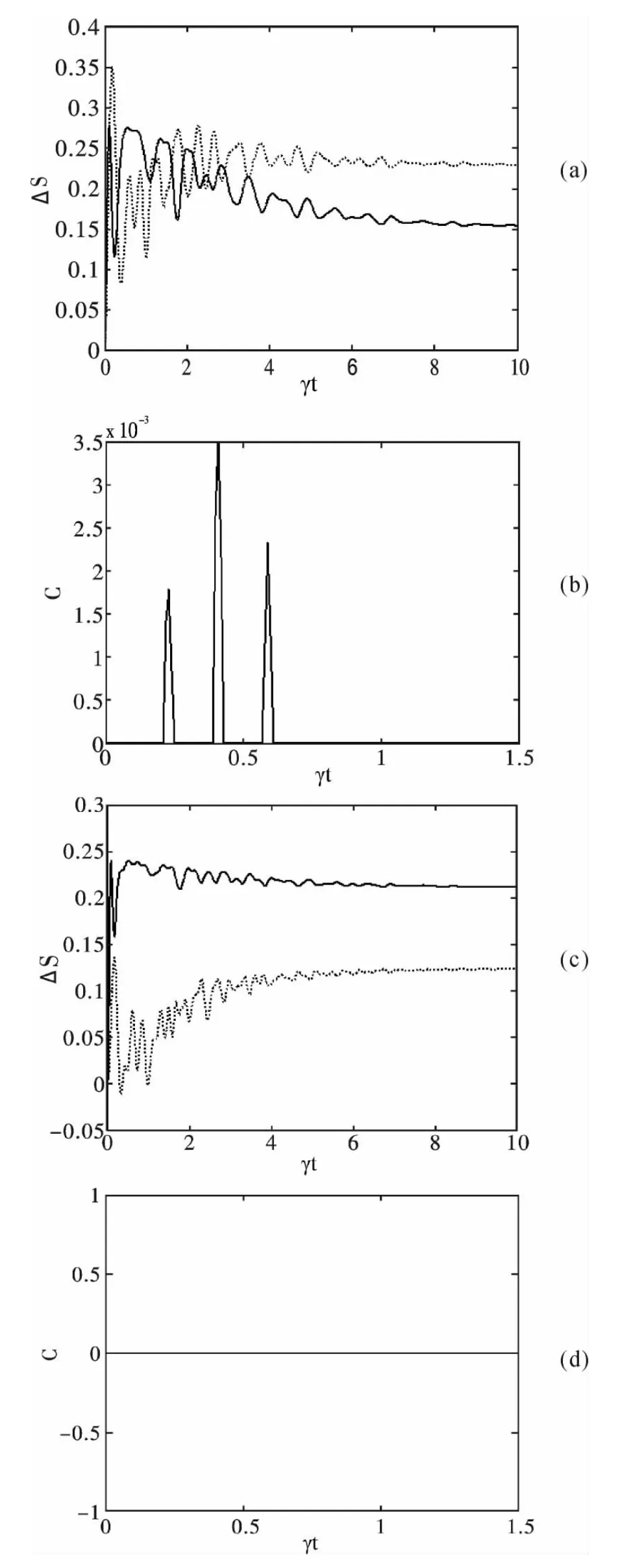
图4 当κ/γ = 20 时,原子与场的熵交换和纠缠度. (a)和(b)Pe = 0.8 ,m = 1.1 ;(c)和(d)Pe = 0.8 ,m= 3.1Fig.4 The atom and field partial entropy changes ΔS(t)and concurrence C against the scales time γt with κ/γ=20.(a)and (b)Pe = 0.8,m = 1.1;(c)and (d)Pe= 0.8,m = 3.1
用我们的理论计算结果作图时发现,当Pe 的值一定时,改变m 的值,总会出现原子与场熵交换现象,但是当Pe 值大于0.45 时,原子与场熵的图像相交错乱. 改变m 值,很难出现原子与场的熵交换的情况. 因此,我们可以得出这样的一个结论,在耗散腔中,存在原子与场发生熵交换的条件为:0 <Pe <0.45,0 <m <5 .
通过对图4 (a)和图4 (c)的比较,我们发现场的平均光子数能影响场与原子的的熵变化.图4 (a)原子的初始态为Pe = 0.8 ,场的初始态为m = 1.1 . 从图中我们可以看到场和原子的熵的曲线没有完全分开,因为某些原因,这两条曲线会在某些时刻处相交. 图4 (b)与图4 (a)原子与场的参数完全相同,我们发现在没有发生完全熵交换的情况下两子系统的纠缠不为零. 原子的初始态不变,场的初始态由1.1 变为3.1 时,在图4 (c)中我们看到原子与场的熵变化完全分开,此时它们之间的纠缠为零见图4 (d)(与原子和场熵交换时的纠缠是一样的). 这与在孤立系统中随着平均光子数的增加,原子与场之间的纠缠在减小的结论是相符的.
5 结 论
利用J-C 模型,我们研究了含有耗散项的两能级原子和单模场的熵变换,发现两者的熵变化存在正相关联和反相关联. 这与无耗散项的两能级原子和单模场的熵关联是一致的,只是在含有耗散项模型的演化过程中,原子与场的熵变化的幅度逐渐减小. 当原子与场的熵交换时,无耗散项的原子与场的熵变化的总和是不变的,即Sa(t)+ Sf(t)= Sf(0)- Sa(0),而在耗散腔的模型中,由于耗散腔不断向外辐射光子,由熵增加原理可知,场的熵变化要比原子的熵变化快一些,即Sa(t)- Sa(0)<- (Sf(t)- Sf(0)). 通过数值计算发现原子与场的熵交换的条件为:0 <Pe <
0.45,0 <m <5 ,在这个范围内,只要选择适当原子初态和场的平均光子数,就可以使得原子的熵和场的熵交换,即两者呈反相关的关系. 当原子与场的熵发生交换时,它们二者的纠缠为零. 原子与场的熵没有完全分开时,它们之间的纠缠是不为零的.
[1] Jaynes E T,Cummings F W. Comparison of quantum and semiclassical radiation theories with application to the beam mase[J]. Proceedings of the IEEE,1963,51:89.
[2] Louisu W H. Quantum statistical properties of radiation[M]. New York:Wiley,1990,323 -328.
[3] Cummings F W. Stimulated emission of radiation in a single mode [J]. Physical Review,1965,140:A1051.
[4] Catani J,Barontini G,Lamporesi G,et al. Entropy exchange in a mixture of ultracold atoms[J]. Phys.Rev. Lett.,2009,103:140401.
[5] Harold M. Entropy exchange in laser cooling [J].Phys. Rev. A ,2008,77:061401.
[6] Apenko S M. Monotonic entropy growth for a nonlinear model of random exchange[J]. Phys. Rev. E,2013,87:024101.
[7] Pandey K C,Efthimios K. Entropy calculation beyond the harmonic approximation:Application to diffusion by concerted exchange in Si[J]. Phys. Rev. Lett.,1991,66:915.
[8] Phoenix S J D,Knight P L. Fluctuations and entropy in model of quantum optical resonance [J]. Ann.Phys. (New York),1988,186:381.
[9] Boukobna E,Tannor D J. Entropy exchange and entanglement in the Jaynes - Cummings model [J].Phys. Rev. A,2005,71:063821.
[10] William K W. Entanglement of formation of an arbitrary state of two qubits[J].Phys. Rev. Lett.,1998,80:2245.
[11] Pan J W,Harald W,Anton Z. Experimental entanglement swapping:entangling photons that never interacted[J].Phys. Rev. Lett.,1998,80:3891.
[12] Olivier M,Bancal J D,Melvyn H,et al. Witnessing trustworthy single-photon entanglement with local homodyne measurements[J]. Phys. Rev. Lett.,2013,110:130401.
[13] Bose S,Fuentes -Guridi I,Knight P L,et al. Subsystem purity as an enforcer of entanglement[J].Phys. Rev. Lett.,2001,87:050401.
[14] Xiang Y,Xiong S J. Entropy exchange,coherent information,and concurrence[J].Phys. Rev. A,2007,76:014306.
[15] Yan X Q,Shao B,Zou J. Entropy exchange and entanglement of an in motion tow - level atom with a quantized field[J]. Chaos Solitons & Fractals ,2006,37:835.
[16] Hu Y H . Entropy exchange and entanglement in intensity-dependent coupling J - C model with atomic motion[J]. Acta Opt. Sin,2012,32:0527002(in Chinese)[胡要花. 运动强度相关耦合J-C 模型中的熵交换和纠缠[J]. 光学学报,2012,32:0527002]
[17] Pendell R,Rajagopal A K. Revival and entanglement from initially entangled mixed states of a damped Jaynes-Cummings model[J]. Phys. Rev. A,2003,67:062110.
[18] Bose S,Fuentes-Guridi,Knight P L,et al. Subsystem purity as an enforcer of entanglement[J]. Phys.Rev. Lett. ,2001,87(5):050401.

