核事故实时释放量集合卡尔曼滤波反演算法研究

唐秀欢，李 华，包利红

（西北核技术研究所，陕西 西安 710024）

福岛核事故后，根据核设施周围的监测数据来反推［1-2］源项的方法即源项反演越来越得到重视。目前核事故源项反演技术有最优插值法［3］、遗传算法［4］、卡尔曼滤波及由其发展的扩展卡尔曼滤波和集合卡尔曼滤波（EnKF）［5-6］等。卡尔曼滤波是一种最优递归资料处理算法，其中EnKF被认为具有较广的应用空间［7］。Astrup等［5-6］采用扩展卡尔曼滤波方法跟踪了单烟团的扩散过程，反演了烟团位置和烟团活度参数，通过EnKF 处理，给出了沉降模块需要的不确定度最佳估计值。Zheng等［8］结合随机游走扩散模型采用EnKF 同化了核素释放率，实验中释放率不确定度减少了80%。文献［9］探讨了卡尔曼滤波反演核事故短时释放率的可行性，给出了卡尔曼滤波基本流程和性能，但由于模式误差的缺失以及线性系统的要求，其应用仍受到较大限制。不同的是，EnKF［10］基于随机动力预测理论发展而来，用蒙特卡罗短期集合预报方法来估计预测误差协方差，具有解决预测误差协方差矩阵估计困难及非线性系统近似等问题的能力。鉴于此，本文研究适用于核事故现场实时释放量快速反演的EnKF基本算法流程，优化EnKF 算法基本参数，为核事故应急源项反演提供新的技术途径。

1 非线性源项状态模型

对于已知的核设施，核事故时泄漏位置容易观测或分析得到，如可能是烟囱、屋顶或安全壳，放射性核素释放量是核应急关注的重点。核设施发生核事故时，设核素释放量状态方程如下：

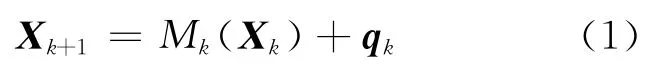
式中：X 为 状态向量；k 为 时 间 段；Mk为 未 知 的变化函数；qk为过程激励噪声。

式（1）表明，核素释放量在各时间段可能是不同的，以释放率表示时，Xk为k 时间段平均释放率；以释放量表示时，Xk为k 时间段积分释放量。

测量方程为非线性方程：

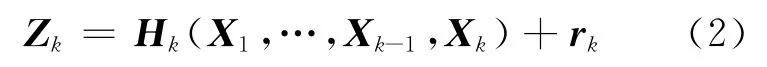
式中：Zk为源项经大气扩散k 时间段后在核设施周围环境地面空气的积分活度浓度测量值；rk为观测噪声；Hk为观测矩阵。

式（2）表明，k时间段前释放的源项对k 时刻的活度浓度依然有影响。

核素大气扩散采用高斯多烟团模型计算［9］，在t时刻，地面空气的瞬时活度浓度与事故源项的释放率、释放时间等有关，假设在t=0时，第i烟团释放出来（时段释放率为Xi），第i烟团在tw时刻即第w 时段在某网格（x，y，0）上的地面空气活度浓度为：

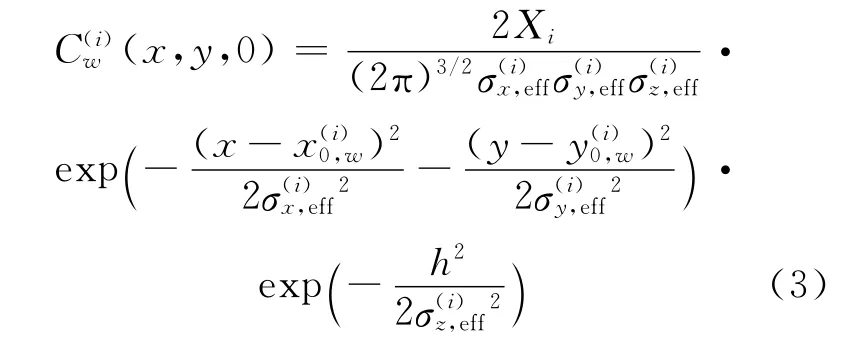
2 EnKF的非线性源项跟踪算法

EnKF反演以核设施周围布置的n 个空间测量点数据为输入，跟踪每个时间段核素释放量，流程如下。

1）产生核事故某时段核素释放量集合成员数为N 的预估计值集合Xi。

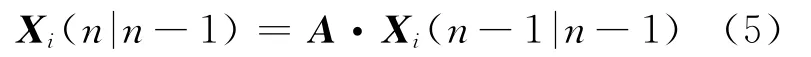
其中：A 为状态转移矩阵，假定事故时释放量恒定，A=1；下标i代表第i个集合成员，取1，…，N；Xi（n|n-1）为利用上一空间测量点预测的核素释放量结果；Xi（n-1|n-1）为上一空间测量点最优的核素释放量结果。

2）计算卡尔曼增益矩阵Kg。EnKF 在计算增益矩阵时直接计算P（n|n-1）·和Hn·P（n|n-1）·。

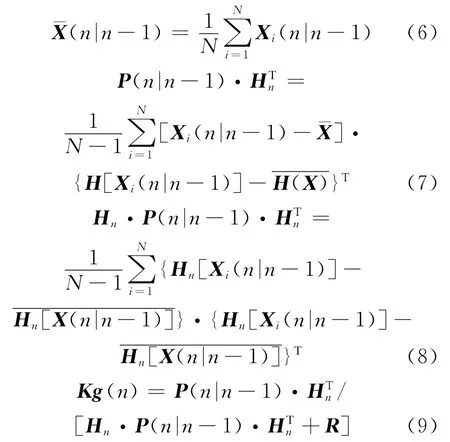
其中，R=E（rn，rn）为观测方程误差协方差矩阵。

3）根据预测值和测量值计算核事故核素释放量，更新估计值X。

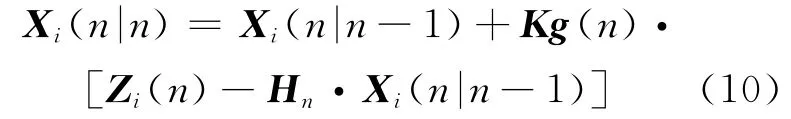
4）进入下一个空间测量点，返回步骤1。

继续使用该时间段上的其他空间测量点数据进行反演，最后计算得到该时间段上的释放量最佳估计值，即为最后一个空间点的N 个分析样本的平均值：

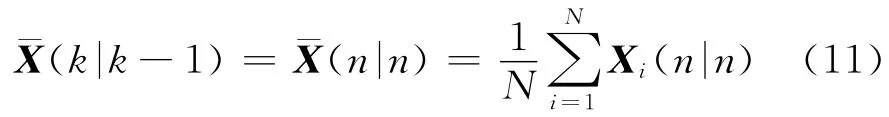
5）进入下一时刻，返回步骤1，连续跟踪到最后观测值产生的时刻。

3 反演仿真结果及分析

3.1 实验参数

为了验证EnKF 方法实时反演核事故核素释放量的可行性及其精度，本文设计了核事故核素释放量随时间推进而变化的反演仿真实验，释放量真值变化如下：1）Q=1010+5×109sin（0.314T）；2）Q=1010+109T。数值实验设计如下：1）假设释放高度为35m，释放时大气稳定度为D 级，10m 高度风速为4 m／s，风向为SE，释放时间为40min；2）核素监测点放置在核设施外半径200、300、400、500、600m处，每个半径按π／4 角度平均布置8 个，共计40个，计算时假设只有下风向及其邻近的监测点响应核事故的核素释放，以核设施为原点，取下风向的3π／4扇面监测点数据为输入，设有效数据点为9个；3）监测数据为释放量真值经大气扩散后在地面1 m 处空气积分活度浓度加入白噪声后所得，假设在事故后4 min 时第一批9个4 min 积分活度浓度内监测数据传回，每隔2min下一批2min积分活度浓度数据传回，每个数据点作一次EnKF 反演，进行数据处理并反演每一时段的事故释放量，最后一个测量点数据反演处理后作为该时段的反演结果；4）R 用过程噪声相对误差10%来计算；5）观测时间段的事故释放量除以每个时间步长得到时段释放率，同时给出观测时段积分释放量和释放率的反演结果。

3.2 实验结果

正弦变化型和直线变化型的源项释放EnKF反演结果以及其反演过程相对误差及各时段最终结果相对误差示于图1。

由图1a可见，在第一批观测点进行EnKF反演后，均可对积分释放量和释放率进行跟踪反演，反演曲线的趋势和量级与真值基本相符。从跟踪效果上看，积分释放量的跟踪总体效果优于释放率的跟踪，原因在于EnKF 反演使用的模型参数是积分释放量。由图1b可见，在第一批数据引入EnKF 反演时，反演过程相对误差较大，随后出现周期性变化。图1c所示的源项随时间不断增大，变化幅度较图1a的剧烈。从反演结果看，EnKF 也能对此类型的释放进行反演，反演曲线的趋势和量级也与真值基本相符。图1d所示反演过程的相对误差与图1b所示的趋势类似，在整个反演过程中均保持同一量级的锯齿形；在每个时段引入新的随机扰动后，该时段反演开始时相对误差最大，反演迭代中逐渐变小，符合EnKF 随机扰动变化的规律。从图1b、d看，每个时段最终积分误差较小，基本控制在5%以内，有效地收敛到真值。图1表明，EnKF能对变化的源项做出反应，对源项目标跟踪具有可行性和有效性。

3.3 集合成员数、空间测量点数对EnKF的影响

取不同集合成员数为10、50、100、150、200，以之为变量，结合不同空间测量点数，研究集合成员数对EnKF分析的影响，结果示于图2。

理论上，EnKF 以基于集合样本的统计量来近似描述真实的统计信息，样本数的选取对模型计算效果的影响是决定性的。根据大数定理，随集合样本数的递增，概率密度函数的误差趋于零，收敛阶为1／N0.5。由图2 可见，空间测量点较多时（图2a），在单一时刻可进行多次EnKF反演，其相对误差均较小，对于不同集合数的反演，所选取的较大样本数并未表现出足够的精度优势；测量点较少时（图2b），每一时刻的反演可能不够充分，相对误差变化较为剧烈，集合成员数为10 时，反演发散，而集合数越大反演效果越好，变化趋势符合大数定理。因此，具有较多的空间测点时，取集合数为50 的EnKF 反演基本取得较佳的反演效果。

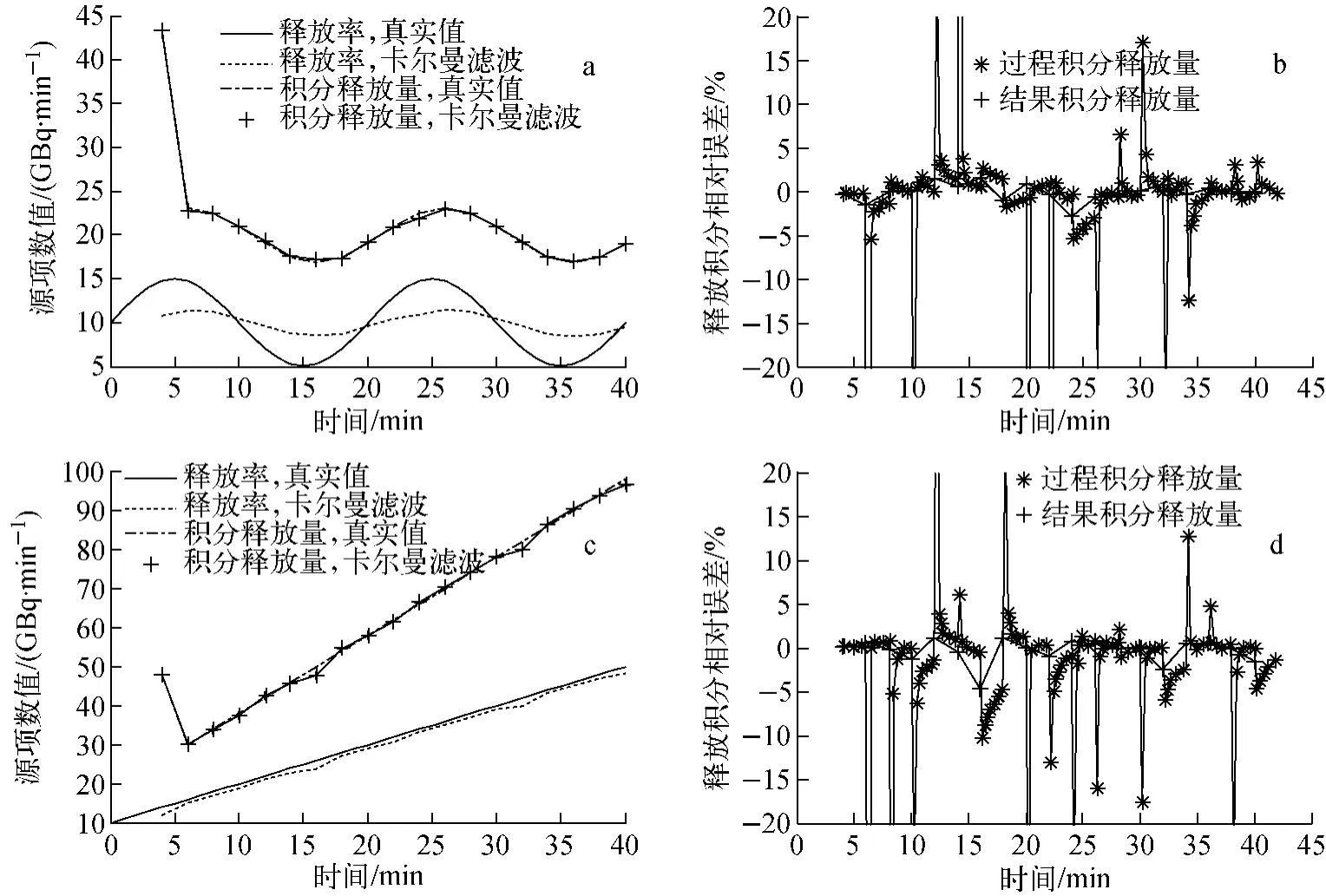
图1 正弦变化型（a，b）和直线变化型（c，d）的源项释放EnKF反演结果Fig.1 EnKF inversion results of sine release（a，b）and linear release（c，d）

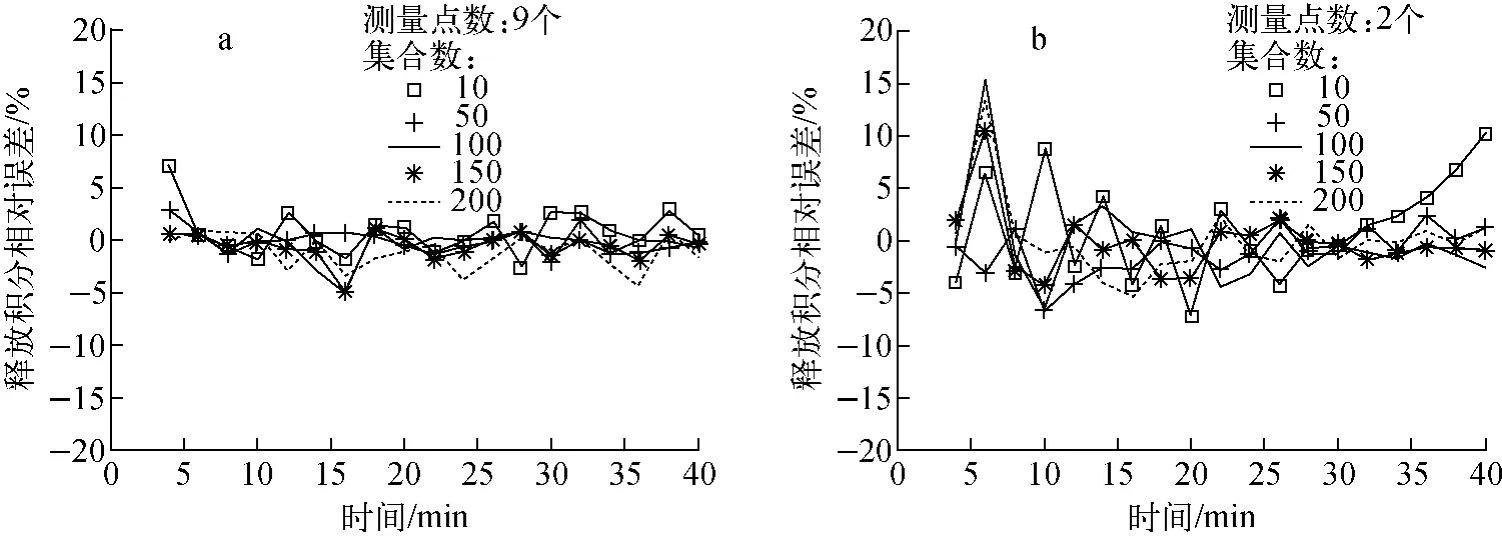
图2 不同集合数对EnKF反演的影响Fig.2 Influence of different ensemble numbers on EnKF inversion

3.4 初始值对EnKF的影响

对初始值的猜测根据来自对事故本身的监测、安全分析的初步判断以及测量点监测数据等，为研究初始值对EnKF 反演的影响，以产生第一批监测数据时刻的释放量源项模拟真值的1／1 000、1／100、1／10、10、100 倍为初始值，观察其对反演结果的影响，结果如图3 所示。由图3可见，以1／1 000源项真值为初始值时，EnKF反演不能跟踪源项的真值，反演所得结果均远小于真值；以1／100源项真值为初始值时，EnKF反演经过一段时间后方能跟踪源项的真值，反演所得结果偏小；以10、100倍源项真值为初始值时，EnKF 反演较易追踪到源项真值。可见，偏大的初始值有利于EnKF 反演。在实际应用中，应根据现场的其他观测结果以及对事故的认识，合理估计偏大的释放初始源项，为EnKF反演提供恰当的初始值。

图3 不同初始值对EnKF反演的影响Fig.3 Influence of different initial values on EnKF inversion

3.5 扰动值、观测误差对EnKF的影响

固定测量相对误差为10%，采用添加随机扰动法对每一时段初期的集合成员进行一次扰动，扰动值取上时刻均值的10、5、2、1、0.5、0.1及0倍，观察扰动值对反演结果的影响。固定扰动值为10倍上时刻均值，取测量相对误差的1 000%、100%、50%、20%、10%、1%及0.1%作为观测误差，观察观测误差对反演结果的影响，结果如图4 所示。由图4a 可见，无扰动（0倍）、较小扰动如0.1倍、0.5倍均值，反演相对误差逐渐增大，反演值趋向于发散；1倍均值扰动反演相对误差保持在10%左右，2、5、10倍扰动反演相对误差总体上基本控制在10%内，但2 倍均值扰动造成的反演相对误差总体较5倍和10倍的大，5倍均值反演过程相对误差局部波动较10 倍的大，10 倍均值扰动反演相对误差最小，即较大扰动值的反演效果较佳。在观测相对误差影响方面，由图4b可见，100%以上相对误差造成反演迭代的发散，20%～50%相对误差造成的反演误差约在10%以内，10%相对误差造成的反演误差则在5%以内，观测相对误差越小则反演精度越高。

3.6 讨论

源项反演还有一些其他的优化技术，如遗传算法、网络神经模拟等［7］，反演的参数、原理、效率也不尽相同，EnKF 的优势在于可实时跟踪源项释放量的变化，较快地完成反演过程。核事故源项释放参数需要反演的可能有释放量、释放高度、释放时间等，就核事故形成的巨大危害辐射场而言，释放量及其随时间的变化是问题的核心。对于其他反演量，如释放高度、释放时间，由于它们之间的相互关系未知，因此多个参数的同时反演存在技术困难，目前只有单个参数的反演是可行的。

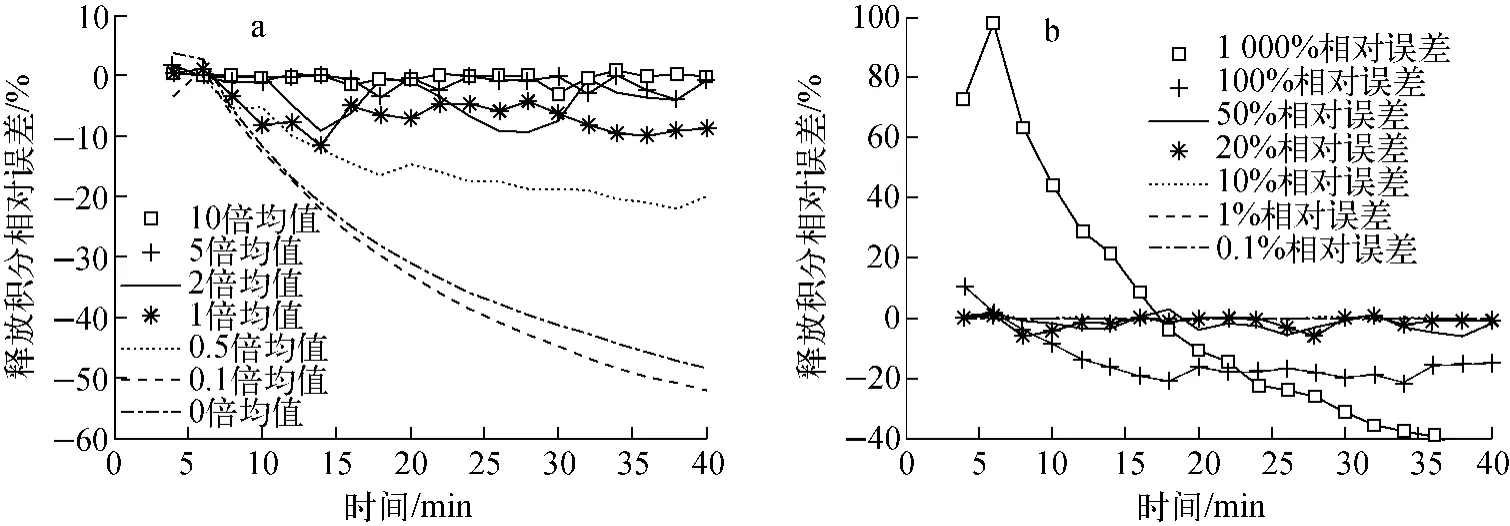
图4 不同扰动值（a）及不同观测相对误差（b）对EnKF反演的影响Fig.4 Influence of different perturbations（a）and observation relative errors（b）on EnKF

离散卡尔曼滤波适用于线性的源项跟踪模型，只适合短期释放的平均释放类型，其反演需要测量误差和模型误差作为输入参数［9］。EnKF可用于非线性源项释放系统，可根据源项释放变化情况追踪其变化率，反演结果虽受模型误差的影响，但无需该参数作为输入，比卡尔曼线性滤波具有优越性。本文反演仿真中释放源项是虚拟设计的，大气高斯多烟团扩散模型是基于正态分布简化的，而在实际应用中会存在一系列的计算误差，如风场不确定性、沉降和化学反应过程近似及模式分辨率等。另外，随时间的延长，源项扩散的烟团数目也逐渐增多，导致了反演计算量的增大。为保证反演尽可能覆盖长的时间段，建议对烟团时间长度进行放大，或对一些远离固定位置的烟团进行记录和过滤，只计算对近期释放的活度浓度贡献较大的烟团。目前，在核事故现场可实时测量的数据多为地面空气γ吸收剂量率，由于核事故释放源项核素多样、化学成分复杂，每种核事故具有不同的核素释放谱，核素发射的射线受现场空间分布的影响，散射、沉积于空气中的能量多样化，地面空气γ吸收剂量率与核事故现场复杂核素的活度浓度还存在着复杂未知的关系。本文采用地面空气积分活度浓度作为测量数据输入，只是在原理上证实了EnKF 技术的可行性和有效性，现场地面空气γ吸收剂量率测量值的输入问题可作为未来研究的重点。

4 结论

本文在源项反演跟踪系统中引入了EnKF技术，建立了与高斯多烟团扩散模型相结合的核事故实时释放量EnKF 基本算法流程。结果显示，集合成员数为50、偏大初始值以及较大扰动值为输入的反演效果较为理想，优化后的流程在虚拟数据反演中积分误差在5%以内。研究表明，核事故实时释放量EnKF 算法具有较好的有效性和可行性，原则上可应用于核事故源项释放量连续实时跟踪反演。

［1］ 陈晓秋，杨端节，李冰.利用福岛第一核电厂事故期间环境监测资料反推事故释放源项［J］.核化学与放射化学，2012，34（2）：83-87.CHEN Xiaoqiu，YANG Duanjie，LI Bing.Reverse estimation of accidental release amounts from Fukushima Daiichi Nuclear Power Plant by environmental monitoring data［J］.Journal of Nuclear and Radiochemistry，2012，34（2）：83-87（in Chinese）.

［2］ 程卫亚，杨宏伟，陈凌，等.利用航测数据反推福岛核事故137Cs的释放量［J］.原子能科学技术，2012，46（2）：252-256.CHENG Weiya，YANG Hongwei，CHEN Ling，et al.Deducing total released activity of137Cs in Fukushima’s nuclear accident by results of airborne monitoring［J］.Atomic Energy Science and Technology，2012，46（2）：252-256（in Chinese）.

［3］ JEONG H J，KIM E H，SUH K S，et al.Determination of the source rate released into the environment from a nuclear power plant［J］.Radiation Protection Dosimetry，2005，113（3）：308-313.

［4］ 宁莎莎，蒯琳萍.混合遗传算法在核事故源项反演中的应用［J］.原子能科学技术，2012，46（增刊）：469-472.NING Shasha，KUAI Linping.Back calculation of source terms by hybrid genetic algorithm in nuclear power plant accident［J］.Atomic Energy Science and Technology，2012，46（Suppl.）：469-472（in Chinese）.

［5］ ASTRUP P，TURCANU C，PUCH R O，et al.Data assimilation in the early phase：Kalman filtering RIMPUFF，RODOS（RA5）-TN（04）-01［R］.Denmark：RisøNational Laboratory Information Service Department，2004.

［6］ PUCH R O，ASTRUP P.An extended Kalman filter methodology for the plume phase of a nuclear accident，RODOS（RA5）-TN（01）-07［R］.Denmark：RisøNational Laboratory Information Service Department，2002.

［7］ 徐志新，奚树人，曲静原.核事故源项反演技术及其研究现状［J］.科技导报，2007，25（5）：16-20.XU Zhixin，XI Shuren，QU Jingyuan.Review on source inversion technology in analyzing nuclear accidents［J］.Science ＆ Technology Review，2007，25（5）：16-20（in Chinese）.

［8］ ZHENG D Q，LEUNG J K C，LEE B Y，et al.Data assimilation in the atmospheric dispersion model for nuclear accident assessments［J］.Atmospheric Environment，2007，41：2 438-2 446.

［9］ 唐秀欢，包利红，李华，等.卡尔曼线性滤波反演核设施核事故中核素释放率的研究［J］.原子能科学技术，2014，48（10）：1 847-1 852.TANG Xiuhuan，BAO Lihong，LI Hua，et al.Radionuclide release rate inversion of nuclear accidents in nuclear facility based on Kalman filter［J］.Atomic Energy Science and Technology，2014，48（10）：1 847-1 852（in Chinese）.

［10］EVENSEN G.The ensemble Kalman filter：Theoretical formulation and practical implementation［J］.Ocean Dynamics，2003，53：343-367.